Giải Toán 9 (Chân trời sáng tạo): Bài tập cuối chương 6

Giải bài tập Toán 9 Bài tập cuối chương 6

Câu hỏi trắc nghiệm

Bài 1 trang 21 Toán 9 Tập 2: Kết luận nào sau đây đúng khi nói về đồ thị của hàm số y = ax² (a ≠ 0)?

A. Với a > 0, đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị.

B. Với a < 0, đồ thị nằm phía dưới trục hoành và O là điểm thấp nhất của đồ thị.

C. Với a > 0, đồ thị nằm phía dưới trục hoành và O là điểm thấp nhất của đồ thị.

D. Với a < 0, đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị.

Lời giải:

Đáp án đúng là: D

Đồ thị của hàm số y = ax² (a ≠ 0):

• Với a > 0, đồ thị nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị.

• Với a < 0, đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị.

Do đó khẳng định D đúng.

Bài 2 trang 21 Toán 9 Tập 2: Điểm nào sau đây thuộc đồ thị hàm số $y=\frac{1}{2}{x}^2?$

A. (4; 4).

B. (−4; 8).

C. (−4; −8).

D. (4; −4).

Lời giải:

Đáp án đúng là: B

• Thay điểm (4; 4) vào đồ thị hàm số $y=\frac{1}{2}{x}^2$, ta có: $\frac{1}{2}{x}^2=\frac{1}{2}\cdot 4^2=8\ne 4.$

Do đó điểm (4; 4) không thuộc đồ thị hàm số $y=\frac{1}{2}{x}^2$.

• Thay điểm (−4; 8) vào đồ thị hàm số $y=\frac{1}{2}{x}^2$, ta có: $\frac{1}{2}{x}^2=\frac{1}{2}\cdot {\left(-4\right)}^2=8.$

Do đó điểm (−4; 8) thuộc đồ thị hàm số $y=\frac{1}{2}{x}^2$.

• Thay điểm (−4; −8) vào đồ thị hàm số $y=\frac{1}{2}{x}^2$, ta có: $\frac{1}{2}{x}^2=\frac{1}{2}\cdot {\left(-4\right)}^2=8\ne -8.$

Do đó điểm (−4; −8) không thuộc đồ thị hàm số $y=\frac{1}{2}{x}^2$.

• Thay điểm (4; −4) vào đồ thị hàm số $y=\frac{1}{2}{x}^2$ , ta có: $\frac{1}{2}{x}^2=\frac{1}{2}\cdot 4^2=8\ne -4.$

Do đó điểm (4; −4) không thuộc đồ thị hàm số $y=\frac{1}{2}{x}^2$ .

Vậy điểm (−4; 8) thuộc đồ thị hàm số $y=\frac{1}{2}{x}^2$

Bài 3 trang 22 Toán 9 Tập 2: Cho hàm số y = 2x². Khi y = 2 thì

A. x = 1.

B. x = 2 hoặc x = −2.

C. x = 1 hoặc x = −1.

D. x = 2.

Lời giải:

Đáp án đúng là: C

Thay y = 2 vào y = 2x², ta được:

2x² = 2

x² = 1

x = ±1.

Vậy x = 1 hoặc x = −1.

Bài 4 trang 22 Toán 9 Tập 2: Đồ thị hàm số y = ax² (a ≠ 0) đi qua điểm (2; −2). Giá trị của a bằng

A. 2.

B. −2.

C. $\frac{1}{2}$.

D. $-\frac{1}{2}$.

Lời giải:

Đáp án đúng là: D

Thay x = 2; y = −2 vào y = ax², ta được −2 = a . 2² hay $a=-\frac{1}{2}.$

Bài 5 trang 22 Toán 9 Tập 2: Nghiệm của phương trình x² − 14x + 13 = 0 là

A. x₁ = −1; x₂ = 13.

B. x₁ = −1; x₂ = −13.

C. x₁ = 1; x₂ = −13.

D. x₁ = 1; x₂ = 13.

Lời giải:

Đáp án đúng là: D

Phương trình x² − 14x + 13 = 0 có a = 1, b = −14, c = 13.

Ta có Δ = (−7)² – 1 . 13 = 36 > 0.

Vậy phương trình có hai nghiệm phân biệt là: $x_1=\frac{7+\sqrt{36}}{1}=13;x_2=\frac{7-\sqrt{36}}{1}=1.$

Bài 6 trang 22 Toán 9 Tập 2: Phương trình nào dưới đây không là phương trình bậc hai một ẩn?

A. $x^2-\sqrt{7}x+7=0.$

B. 3x² + 5x – 2 = 0.

C. 2x² – 2 365 = 0.

D. –7x + 25 = 0.

Lời giải:

Đáp án đúng là: D

Phương trình –7x + 25 = 0 không phải phương trình bậc hai một ẩn vì –7x + 25 = 0 chính là phương trình 0x² – 7x + 25 = 0 với x² có hệ số a = 0.

Bài 7 trang 22 Toán 9 Tập 2: Gọi S và P lần lượt là tổng và tích của hai nghiệm của phương trình x² + 5x – 10 = 0. Khi đó giá trị của S và P là

A. S = 5; P = 10.

B. S = –5; P = 10.

C. S = –5; P = –10.

D. S = 5; P = –10.

Lời giải:

Đáp án đúng là: C

Ta có $S=x_1+x_2=-\frac{b}{a}=-5;P=x_1\cdot x_2=\frac{c}{a}=-10.$

Bài 8 trang 22 Toán 9 Tập 2: Cho phương trình x² + 7x – 15 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Khi đó giá trị của biểu thức $x_1^2+x_2^2-x_1{x}_2$ là

A. 79.

B. 94.

C. –94.

D. –79.

Lời giải:

Đáp án đúng là: B

Phương trình x² + 7x – 15 = 0 có ∆ = 7² – 4 . 1 . (–15) = 109 > 0 nên nó có hai nghiệm phân biệt x₁, x₂.

Theo định lí Viète, ta có: $x_1+x_2=\frac{-b}{a}=-7;x_1\cdot x_2=\frac{c}{a}=-15.$

Ta có $x_1^2+x_2^2-x_1{x}_2=x_1^2+2x_1{x}_2+x_2^2-3x_1{x}_2$

$={\left(x_1+x_2\right)}^2-3x_1{x}_2$= (–7)² – 3 . (–15) = 94.

Vậy $x_1^2+x_2^2-x_1{x}_2=94.$

Bài tập tự luận

Bài 9 trang 22 Toán 9 Tập 2: Cho hai hàm số: $y=\frac{3}{2}{x}^2$ và y = –x². Vẽ đồ thị của hai hàm số đã cho trên cùng mặt phẳng tọa độ Oxy.

Lời giải:

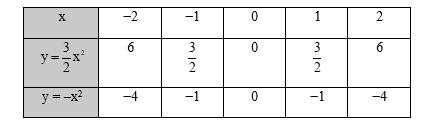
Ta có bảng giá trị của hàm số:

Trên mặt phẳng tọa độ, lấy các điểm $A\left(-2;6\right),B\left(-1;\frac{3}{2}\right),O\left(0;0\right),C\left(1;\frac{3}{2}\right),D\left(2;6\right),$

A'(−2; −4), B'(−1; −1), C'(1; −1), D'(2; −4).

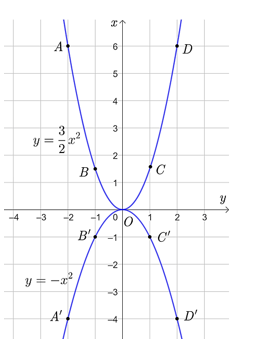
• Đồ thị hàm số $y=\frac{3}{2}{x}^2$ là một đường parabol đỉnh O, đi qua các điểm $B\left(-1;\frac{3}{2}\right),O\left(0;0\right),C\left(1;\frac{3}{2}\right),D\left(2;6\right).$

• Đồ thị hàm số y = –x² là một đường parabol đỉnh O, đi qua các điểm A'(−2; −4), B'(−1; −1), C'(1; −1), D'(2; −4).

Ta có đồ thị của hai hàm số hai hàm số $y=\frac{3}{2}{x}^2$ và y = –x² được vẽ trên cùng một mặt phẳng tọa độ Oxy như sau:

Bài 10 trang 22 Toán 9 Tập 2: Cho hàm số y = ax² (a ≠ 0)

a) Tìm a để đồ thị hàm số đi qua điểm M(2; 2).

b) Vẽ đồ thị (P) của hàm số với a vừa tìm được.

c) Tìm các điểm thuộc đồ thị (P) có tung độ y = 8.

Lời giải:

a) Thay x = 2; y = 2 vào hàm số y = ax² (a ≠ 0), ta được: 2 = a . 2² suy ra $a=\frac{1}{2}$ .

b) Từ câu a, ta có $a=\frac{1}{2}$ nên đồ thị hàm số cần tìm là $y=\frac{1}{2}{x}^2$ .

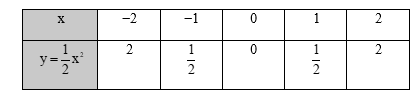
Ta có bảng giá trị:

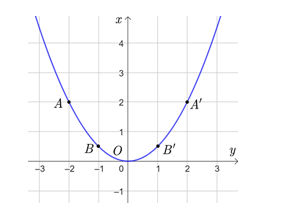
Trên mặt phẳng tọa độ, lấy các điểm $A\left(-2;2\right),B\left(-1;\frac{1}{2}\right),O\left(0;0\right),B^{\text{'}}\left(1;\frac{1}{2}\right),A^{\text{'}}\left(2;2\right).$

Đồ thị hàm số $y=\frac{1}{2}{x}^2$ là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.

c) Thay y = 8 vào $y=\frac{1}{2}{x}^2$, ta được:

$8=\frac{1}{2}{x}^2$

x² = 16

x = ±4.

Vậy có hai điểm thuộc đồ thị là: (−4; 8), (4; 8).

Bài 11 trang 22 Toán 9 Tập 2: Giải các phương trình:

a) x² – 12x = 0;

b) 13x² + 25x – 38 = 0;

c) $3x^2-4\sqrt{3}x+4=0;$

d) x(x + 3) = 27 – (11 – 3x).

Lời giải:

a) x² – 12x = 0

x(x – 12) = 0

x = 0 hoặc x – 12 = 0

x = 0 hoặc x = 12.

Vậy phương trình có 2 nghiệm là x = 0 và x = 12.

b) 13x² + 25x – 38 = 0

Phương trình 13x² + 25x – 38 = 0 có a + b + c = 13 + 25 – 38 = 0.

Vậy phương trình có hai nghiệm là $x_1=1;x_2=\frac{c}{a}=-\frac{38}{13}.$

c) $3x^2-4\sqrt{3}x+4=0$

Ta có ${\Delta }^{\text{'}}={\left(-2\sqrt{3}\right)}^2-4\cdot 3=0$ .

Vậy phương trình có nghiệm kép $x_1=x_2=\frac{4\sqrt{3}}{2\cdot 3}=\frac{2\sqrt{3}}{3}.$

d) x(x + 3) = 27 – (11 – 3x)

x² + 3x = 27 – 11 + 3x

x² = 16

x = ±4.

Vậy phương trình có 2 nghiệm là x = ±4.

Bài 12 trang 23 Toán 9 Tập 2: Tính nhẩm nghiệm của các phương trình sau và kiểm tra kết quả bằng máy tính cầm tay.

a) 14x² – 13x – 27 = 0;

b) 5,4x² + 8x + 2,6 = 0;

c) $\frac{2}{3}{x}^2+2x-\frac{8}{3}=0;$

d) $3x^2-\left(3+\sqrt{5}\right)x+\sqrt{5}=0.$

Lời giải:

a) Phương trình 14x² – 13x – 27 = 0 có a – b + c = 14 – 13 – 27 = 0.

Vậy phương trình có hai nghiệm là $x_1=-1;x_2=-\frac{c}{a}=\frac{27}{14}.$

b) Phương trình 5,4x² + 8x + 2,6 = 0 có a – b + c = 5,4 – 8 + 2,6 = 0.

Vậy phương trình có hai nghiệm là $x_1=-1;x_2=-\frac{c}{a}=-\frac{2,6}{5,4}=-\frac{13}{27}.$

c) Phương trình $\frac{2}{3}{x}^2+2x-\frac{8}{3}=0$ có $a+b+c=\frac{2}{3}+2-\frac{8}{3}=0$.

Vậy phương trình có hai nghiệm là $x_1=1;x_2=\frac{c}{a}=-\frac{8}{3}:\frac{2}{3}=-4.$

d) Phương trình $3x^2-\left(3+\sqrt{5}\right)x+\sqrt{5}=0$ có $a+b+c=3-\left(3+\sqrt{5}\right)+\sqrt{5}=0$ .

Vậy phương trình có hai nghiệm là $x_1=1;x_2=\frac{c}{a}=\frac{\sqrt{5}}{3}.$

Bài 13 trang 23 Toán 9 Tập 2: Tìm hai số u và v trong mỗi trường hợp sau:

a) u + v = –2; uv = –35;

b) u + v = 8; uv = –105.

Lời giải:

a) Điều kiện để có hai số đó là: S² − 4P ≥ 0 suy ra (–2)² – 4 . (–35) = 144 ≥ 0.

Hai số cần tìm là nghiệm của phương trình x² + 2x – 35 = 0.

Ta có ${\Delta }^{\text{'}}=1^2-1\cdot \left(-35\right)=36>0;\sqrt{{\Delta }^{\text{'}}}=\sqrt{36}=6.$

Suy ra $u=\frac{-1+6}{1}=5;v=\frac{-1-6}{1}=-7.$

Vậy hai số cần tìm là 5 và –7.

b) Điều kiện để có hai số đó là: S² − 4P ≥ 0 suy ra 8² – 4 . (–105) = 484 ≥ 0.

Hai số cần tìm là nghiệm của phương trình x² – 8x – 105 = 0.

Ta có ${\Delta }^{\text{'}}={\left(-4\right)}^2-1\cdot \left(-105\right)=121>0;\sqrt{{\Delta }^{\text{'}}}=\sqrt{121}=11.$

Suy ra $u=\frac{4+11}{1}=15;v=\frac{4-11}{1}=-7.$

Vậy hai số cần tìm là 15 và –7.

Bài 14 trang 23 Toán 9 Tập 2: Cho phương trình 2x² – 7x + 6 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của biểu thức $A=\left(x_1+2x_2\right)\left(x_2+2x_1\right)-x_1^2{x}_2^2.$

Lời giải:

Phương trình 2x² – 7x + 6 = 0 có ∆ = (–7)² – 4 . 2 . 6 = 1 > 0 nên nó có hai nghiệm phân biệt x₁, x₂.

Theo định lí Viète, ta có: $x_1+x_2=\frac{-b}{a}=\frac{7}{2};x_1\cdot x_2=\frac{c}{a}=3.$

Ta có $A=\left(x_1+2x_2\right)\left(x_2+2x_1\right)-x_1^2{x}_2^2$

$=x_1{x}_2+2x_1^2+2x_2^2+4x_1{x}_2-x_1^2{x}_2^2$

$=2\left(x_1^2+2x_1{x}_2+x_2^2\right)-{\left(x_1{x}_2\right)}^2+x_1{x}_2$

$=2{\left(x_1+x_2\right)}^2-{\left(x_1{x}_2\right)}^2+x_1{x}_2$

$=2\cdot {\left(\frac{7}{2}\right)}^2–3^2+3=\frac{37}{2}.$

Vậy $A=\left(x_1+2x_2\right)\left(x_2+2x_1\right)-x_1^2{x}_2^2=\frac{37}{2}.$

Bài 15 trang 23 Toán 9 Tập 2: Một người đi xe đạp từ A đến B cách nhau 24 km. Khi đi từ B trở về A, nhờ xuôi gió nên tốc độ lúc về nhanh hơn tốc độ lúc đi là 4 km/h, vì thế thời gian về ít hơn thời gian đi 30 phút. Tính tốc độ của xe đạp khi đi từ A đến B.

Lời giải:

Gọi tốc độ của xe đạp đi từ A đến B là x (km/h) (x > 0).

Suy ra tốc độ của xe đạp đi từ A đến B là x + 4 (km/h).

Thời gian xe đạp đi từ A đến B là: $\frac{24}{x}$ (giờ).

Thời gian xe đạp đi từ B đến A là: $\frac{24}{x+4}$ (giờ).

Vì thời gian đi từ B đến A nhanh hơn đi từ A đến B là 30 phút $=\frac{1}{2}$ giờ nên ta có phương trình: $\frac{24}{x}-\frac{24}{x+4}=\frac{1}{2}$.

Biến đổi phương trình trên, ta được:

24 . 2(x + 4) – 24 . 2x = x(x + 4) hay x² + 4x – 192 = 0.

Giải phương trình trên, ta được: x₁ = 12 (thỏa mãn), x₂ = −16 (loại).

Vậy tốc độ của xe đạp đi từ A đến B là 12 km/h.

Bài 16 trang 23 Toán 9 Tập 2: Một đội thợ mỏ phải khai thác 216 tấn than trong một thời gian nhất định. Ba ngày đầu , mỗi ngày khai thác theo đúng định mức. Sau đó, mỗi ngày họ đều khai thác vượt mức 8 tấn. Do đó họ đã khai thác được 232 tấn và xog trước thời hạn 1 ngày. Hỏi theo kế hoạch, mỗi ngày đội thợ phải khai thác bao nhiêu tấn than?

Lời giải:

Gọi x (tấn) là lượng than mà đội khai thác mỗi ngày theo kế hoạch (x > 0).

Sau 3 ngày đầu, mỗi ngày đội khai thác x + 8 (tấn).

Thời gian dự định khai thác là $\frac{216}{x}$ (ngày).

Lượng than khai thác 3 ngày đầu là 3x (tấn)

Lượng than khai thác trong những ngày còn lại là 232 – 3x (tấn)

Thời gian đội khai thác 232 – 3x tấn than là: $\frac{232-3x}{x+8}$ (ngày).

Theo bài ra ta có phương trình: $\frac{216}{x}-1=3+\frac{232-3x}{x+8}$

Biến đổi phương trình trên, ta được: x² + 48x – 1 728 = 0.

Giải phương trình trên, ta được: x₁ = 24 (thỏa mãn), x₂ = −72 (loại).

Vậy theo kế hoạch, mỗi ngày đội thợ phải khai thác 24 tấn than.

Bài 17 trang 23 Toán 9 Tập 2: Một miếng kim loại thứ nhất nặng 585 g, miếng kim loại thứ hai nặng 420 g. Thể tích của miếng thứ nhất nhỏ hơn thể tích của miếng thứ hai là 10 cm³, nhưng khối lượng riêng của miếng thứ nhất lớn hơn khối lượng riêng của miếng thứ hai là 9 g/cm³. Biết công thức tính khối lượng riêng của một vật là $D=\frac{m}{V},$ trong đó: D (g/cm³) là khối lượng riêng, m (g) là khối lượng của vật, V (cm³) là thể tích của vật. Tìm khối lượng riêng của mỗi miếng kim loại.

Lời giải:

Gọi x là thể tích miếng kim loại thứ nhất (x > 0).

Suy ra thể tích miếng kim loại thứ hai là x + 10 (cm³).

Khối lượng riêng của miếng kim loại thứ nhất là: $\frac{585}{x}$(g/cm³).

Khối lượng riêng của miếng kim loại thứ hai là: $\frac{420}{x+10}$ (g/cm³).

Theo bài ra ta có phương trình: $\frac{585}{x}-\frac{420}{x+10}=9.$

Biến đổi phương trình trên, ta được: 9x² − 75x − 5 850 = 0.

Giải phương trình trên, ta được: x₁ = 30 (thỏa mãn), $x_2=-\frac{65}{3}$ (loại).

Vậy khối lượng riêng của miếng kim loại thứ nhất là $\frac{585}{30}=19,5$ g/cm³ và khối lượng riêng của miếng kim loại thứ hai là $\frac{420}{30+10}=10,5$ g/cm³.

Bài 18 trang 23 Toán 9 Tập 2: Hai dung dịch muối có tổng khối lượng bằng 220 kg. Lượng muối trong dung dịch I là 5 kg, lượng muối trong dung dịch II là 4,8 kg. Biết nồng độ muối trong dung dịch I nhiều hơn nồng độ muối trong dung dịch II là 1%. Tính khối lượng mỗi dung dịch nói trên.

Lời giải:

Gọi khối lượng dung dịch I là x (kg) (0 < x < 220).

Khối lượng dung dịch II là 220 – x (kg).

Theo bài ra ta có phương trình: $\frac{5}{x}-\frac{4,8}{220-x}=\frac{1}{100}.$

Biến đổi phương trình trên, ta được: x² – 1 200x + 11 000 = 0.

Giải phương trình trên, ta được: x₁ = 100 (thỏa mãn), x₂ = 1 100 (loại).

Vậy khối lượng dung dịch I là 100 kg và khối lượng dung dịch II là 120 kg.

Xem thêm Lời giải bài tập Toán 9 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 6

Bài 1: Bảng tần số và biểu đồ tần số

Bài 2: Bảng tần số tương đối và biểu đồ tần số tương đối

Bài 3: Biểu diễn số liệu ghép nhóm

Bài tập cuối chương 7