Giải Toán 9 Bài 1 (Chân trời sáng tạo): Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

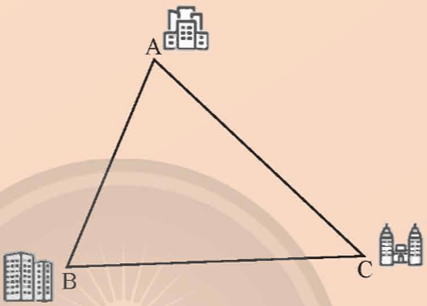
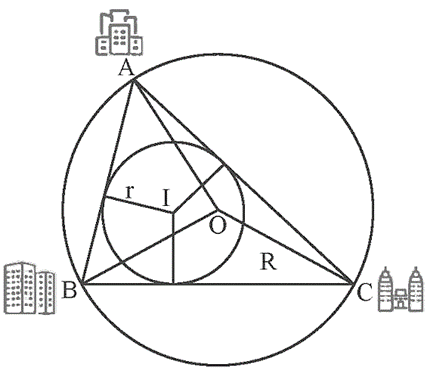
Khởi động trang 65 Toán 9 Tập 2: Ba cụm dân cư A, B, C nối với nhau bởi ba con đường AB, BC, CA như hình dưới đây. Người ta muốn tìm địa điểm O để xây một trường học và địa điểm I cách đều ba con đường. Làm thế nào để xác định hai điểm O và I?

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

− Vị trí điểm O để xây trường học cần cách đều 3 điểm A, B, C nên O là tâm đường tròn ngoại tiếp tam giác ABC.

− Vị trí điểm I để lập trạm cứu hộ cần cách đều 3 con đường AB, BC, CA nên I là tâm đường tròn nội tiếp tam giác ABC.

1. Đường tròn ngoại tiếp tam giác

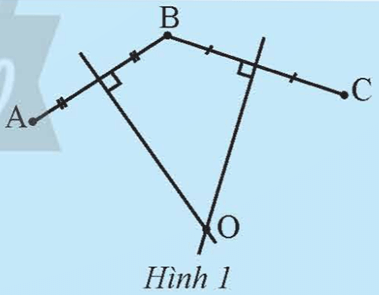
Khám phá 1 trang 65 Toán 9 Tập 2: Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung trực của đoạn thẳng AB và BC (Hình 1).

a) So sánh độ dài của đoạn thẳng OA, OB và OC.

b) Vẽ đường tròn đi qua ba điểm A, B, C.

Lời giải:

a) Vì O thuộc đường trung trực của AB.

Suy ra OA = OB (tính chất đường trung trực) (1).

Vì O thuộc đường trung trực của BC.

Suy ra OC = OB (tính chất đường trung trực) (2).

Từ (1) và (2) suy ra OA = OB = OC.

b) Từ câu a, ta có OA = OB = OC nên O là tâm đường tròn đi qua ba điểm A, B, C.

Ta có đường tròn đi qua ba điểm A, B, C như hình vẽ.

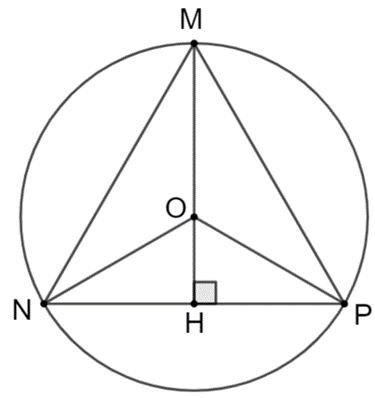
Thực hành 1 trang 67 Toán 9 Tập 2: Xác định tâm và bán kính của đường tròn ngoại tiếp mỗi tam giác sau:

a) Tam giác đều MNP có cạnh bằng 4;

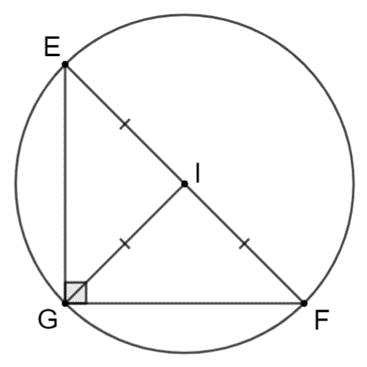
b) Tam giác EFG có EF = 5 cm; EG = 3 cm; FG = 4 cm.

Lời giải:

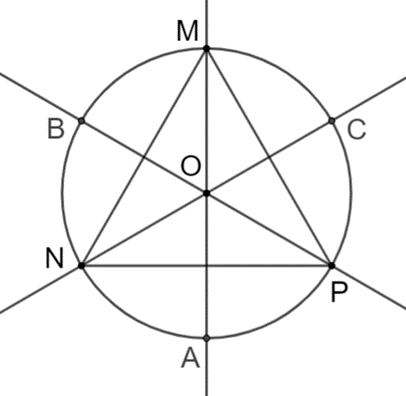
a) Vẽ đường cao MH của giác MNP, gọi O là điểm nằm trên MH sao cho OM = $\frac{2}{3}$MH.

Do tam giác MNP đều nên O vừa là trọng tâm vừa là giao điểm của ba đường trung trực.

Bán kính đường tròn ngoại tiếp tam giác MNP là:

R = OH = $\frac{a\sqrt{3}}{3}=\frac{4\sqrt{3}}{3}\left(cm\right).$

Do đó, đường tròn ngoại tiếp tam giác đều MNP có tâm O và bán kính $R=\frac{4\sqrt{3}}{3}cm.$

Ta có hình vẽ:

b) Xét tam giác EFG có 5² = 3² + 4² nên EF² = EG² + FG².

Suy ra tam giác EFG vuông tại G.

Gọi I là trung điểm của cạnh huyền EF.

Ta có GI là đường trung tuyến ứng với cạnh huyền của tam giác EFG vuông tại G.

Suy ra IG = IE = IF = $\frac{EF}{2}$ = 2,5 (cm).

Do đó, đường tròn tâm I bán kính 5 cm ngoại tiếp tam giác EFG.

Ta có hình vẽ:

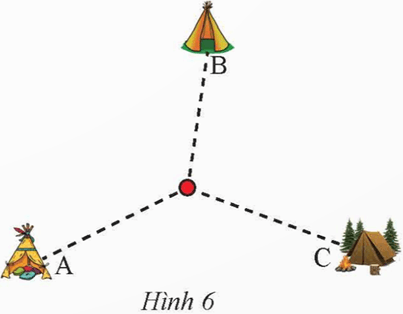
Vận dụng 1 trang 67 Toán 9 Tập 2: Có ba tổ dựng lều ở ba vị trí A, B, C như Hình 6. Ban tổ chức đặt ba thùng có dung tích bằng nhau tại một điểm tập kết chung. Mỗi tổ có sáu người, được phát một chiếc gàu giống nhau, các thành viên trong tổ chia thành từng cặp cõng nhau, múc nước từ tại của mình về đổ vào thùng tại điểm tập kết. Thùng của tổ nào đầy trước thì tổ đó chiến thắng. Để trò chơi công bằng, cần tìm điểm tập kết cách đều ba lều. Hãy xác định điểm đó.

Lời giải:

Điểm tập kết cách đều 3 lều tức khoảng cách từ điểm tập kết đều mỗi lều là như nhau tam giác.

Do đó, điểm tập kết là tâm đường tròn ngoại tiếp tam giác có 3 đỉnh là vị trí của ba trại.

2. Đường tròn nội tiếp tam giác

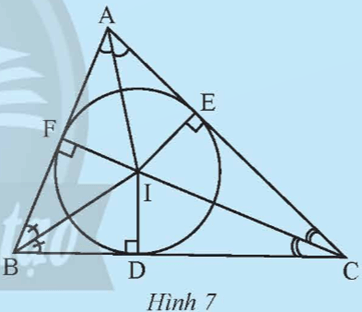
Khám phá 2 trang 67 Toán 9 Tập 2: Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7).

a) Chứng minh rằng IE = IF = ID.

b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?

Lời giải:

a) Xét ΔFBI vuông tại F và ΔDBI vuông tại D có:

$\widehat{FBI}=\widehat{IBD}$ (do BI là phân giác góc $\widehat{FBD}$);

IB chung.

Do đó ΔFBI = ΔDBI (cạnh huyền – góc nhọn).

Suy ra IF = ID (hai cạnh tương ứng) (1).

Xét ΔIDC vuông tại D và ΔIEC vuông tại E có:

$\widehat{DCI}=\widehat{IEC}$ (do IC là phân giác góc $\widehat{DEC}$);

IC chung.

Do đó ΔIDC = ΔIEC (cạnh huyền – góc nhọn).

Suy ra ID = IE (hai cạnh tương ứng) (2).

Từ (1) và (2) suy ra IE = IF = ID.

b) Đường tròn này tiếp xúc với ba cạnh của tam giác tại các điểm F, D, E.

Thực hành 2 trang 68 Toán 9 Tập 2: Xác định tâm và bán kính đường tròn nội tiếp tam giác đều MNP có độ dài cạnh bằng 8 cm.

Lời giải:

Gọi O là giao điểm của đường cao MA, NP và PC của tam giác MNP.

Ta có tam giác MNP đều nên MA, NB, PC là ba đường trung tuyến đồng thời là ba đường phân giác của tam giác.

Do đó, O là trọng tâm, đồng thời là tâm đường tròn nội tiếp tam giác MNP với bán kính r = OA = OB = OC.

Bán kính đường tròn ngoại tiếp tam giác là $r=\frac{1}{3}\cdot \frac{8\sqrt{3}}{2}=\frac{4\sqrt{3}}{3}\left(cm\right).$

Do đó, đường tròn nội tiếp tam giác đều MNP có tâm O và bán kính $r=\frac{4\sqrt{3}}{3}cm$ như hình vẽ.

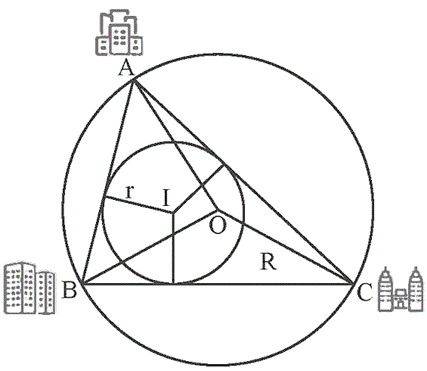
Vận dụng 2 trang 68 Toán 9 Tập 2: Theo gợi ý trong Hình 10, nêu cách xác định hai điểm I và O của tình huống trong Hoạt động khởi động (trang 65).

Lời giải:

− Vị trí điểm O để xây trường học cần cách đều 3 điểm A, B, C nên O là tâm đường tròn ngoại tiếp tam giác ABC.

− Vị trí điểm I để lập trạm cứu hộ cần cách đều 3 con đường AB, BC, CA nên I là tâm đường tròn nội tiếp tam giác ABC.

Bài tập

Bài 1 trang 68 Toán 9 Tập 2: Cho tam giác đều ABC có cạnh bằng 6 cm.

a) Nêu các vẽ đường tròn ngoại tiếp tam giác ABC.

b) Nêu các vẽ đường tròn nội tiếp tam giác ABC.

c) Tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.

Lời giải:

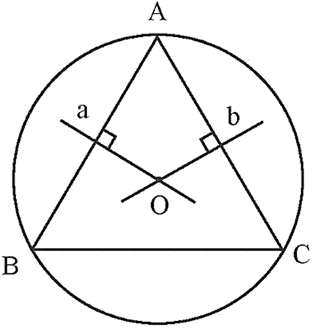
a) Cách vẽ đường tròn ngoại tiếp tam giác ABC:

− Vẽ đường trung trực a của đoạn thẳng AB.

− Vẽ đường trung trực b của đoạn thẳng AC.

− Gọi O là giao điểm của a và b.

− Vẽ đường tròn tâm O bán kính OA.

Khi đó, đường tròn (O; OA) là đường tròn ngoại tiếp tam giác ABC.

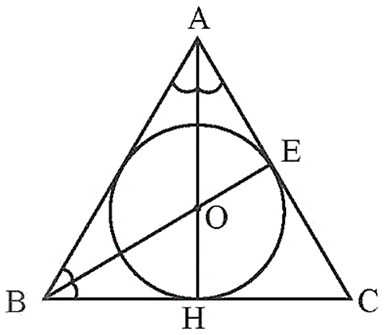
b) Cách vẽ đường tròn nội tiếp tam giác ABC:

− Vẽ đường phân giác AH của góc BAC.

− Vẽ đường phân giác BE của góc ABC.

− Gọi O là giao điểm của AH và BE.

− Vẽ đường tròn tâm O bán kính OH.

Khi đó, đường tròn (O; OH) là đường tròn nội tiếp tam giác ABC.

c) Vì tam giác ABC đều nên O cũng là trọng tâm của ∆ABC.

Theo định lí Pythagore, ta có: AB² = AH² + BH².

Suy ra $AH=\sqrt{AB{}_2-BH{}_2}=\sqrt{6{}_2-3{}_2}=3\sqrt{3}\left(cm\right).$

Bán kính đường tròn ngoại tiếp tam giác ABC là:

$R=OA=\frac{2}{3}AH=\frac{2}{3}\cdot 3\sqrt{3}=2\sqrt{3}\left(cm\right).$

Bán kính đường tròn nội tiếp tam giác ABC là:

$r=OH=\frac{1}{3}AH=\frac{1}{3}\cdot 3\sqrt{3}=\sqrt{3}\left(cm\right).$

Vậy $R=2\sqrt{3}cm;r=\sqrt{3}cm.$

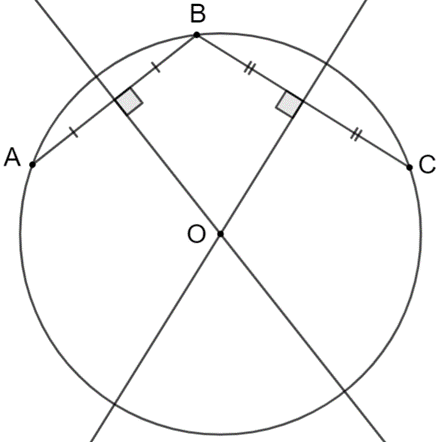
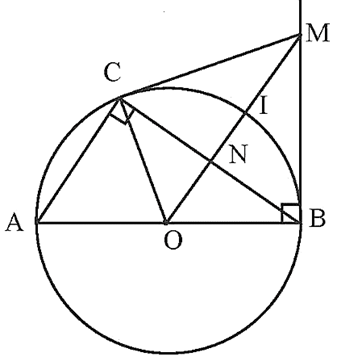
Bài 2 trang 69 Toán 9 Tập 2: Cho tam giác ABC (AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB).

a) Chứng minh OI vuông góc với BC.

b) Vẽ tiếp tuyến của đường tròn (O) tại B và cắt OI tại M. Chứng minh MC là tiếp tuyến của đường tròn (O).

Lời giải:

a) Ta có $\widehat{ACB}=90°$ (góc nội tiếp chắn nửa đường tròn), suy ra AC ⊥ BC.

Mà AC // OI nên OI ⊥ BC (tính chất từ vuông góc đến song song).

b) Gọi N là giao điểm của BC và OI.

Tam giác OBC có OB = OC = R nên ∆OBC cân tại O.

Ta có ON là đường cao của ∆OBC cân tại O.

Suy ra ON cũng là đường phân giác của $\widehat{COB}$.

Do đó $\widehat{CON}=\widehat{NOB}.$

Xét ∆COM và ∆BOM có:

OM là cạnh chung; $\widehat{COM}=\widehat{MOB};$ OB = OC = R.

Do đó ∆COM = ∆BOM (c.g.c).

Suy ra $\widehat{OCM}=\widehat{OBM}$ (hai góc tương ứng).

Mà $\widehat{OBM}=90°$ (BM là tiếp tuyến của đường tròn (O) tại B).

Suy ra $\widehat{OCM}=\widehat{OBM}=90°$ nên OC ⊥ MC tại C.

Mà C thuộc đường tròn (O), do đó MC là tiếp tuyến của đường tròn (O).

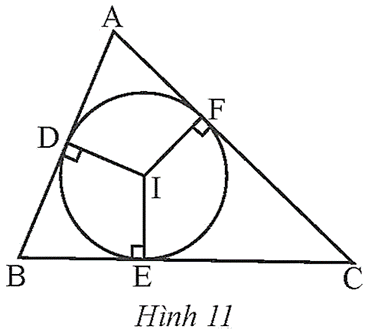
Bài 3 trang 69 Toán 9 Tập 2: Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11).

a) Chứng minh 2AD = AB + AC – BC.

b) Tìm các hệ thức tương tự như ở câu a.

Lời giải:

a) Theo tính chất hai tiếp tuyến cắt nhau, ta có: AD = AF, BD = BE, CE = CF.

Suy ra AB + AC – BC = (AD + BD) + (AF + CF) – (BE + CE)

          = (AD + AF) + (CF – CE) + (BD – BE) = 2AD.

Vậy 2AD = AB + AC – BC (đpcm).

b) Các hệ thức tương tự như ở câu a là:

2AF = AB + AC – BC;

2BD = 2BE = AB + BC – AC;

2EC = 2FC = AC + BC – AB.

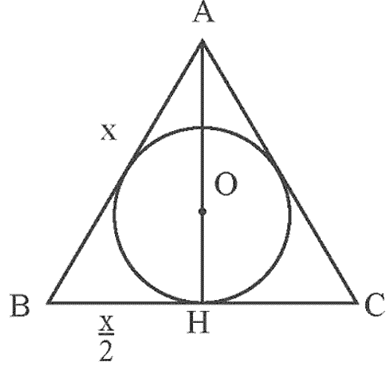
Bài 4 trang 69 Toán 9 Tập 2: Tính diện tích tam giác đều có bán kính đường tròn nội tiếp bằng 1 cm.

Lời giải:

Gọi (O; 1 cm) là đường tròn nội tiếp tam giác đều ABC có cạnh bằng x (cm) (x > 0).

Khi đó O là trọng tâm của ∆ABC.

Vẽ đường trung tuyến AH của ∆ABC.

Ta có r = $\frac{1}{3}$AH, suy ra AH = 3r = 3 . 1 = 3 (cm).

Theo định lí Pythagore, ta có AB² = AH² + HB².

Suy ra $x^2=3^2+{\left(\frac{x}{2}\right)}^2$ nên $x^2-\frac{x^2}{4}=9$ hay x² = 12.

Do đó x = -2$\sqrt{3}$ (loại) hoặc x = 2$\sqrt{3}$ (thỏa mãn).

Diện tích tam giác ABC là:

$S=\frac{1}{2}AH\cdot BC=\frac{1}{2}\cdot 3\cdot 2\sqrt{3}=3\sqrt{3}\left(c{m}^2\right)$.

Vậy diện tích tam giác đều cần tìm là $3\sqrt{3}c{m}^2.$

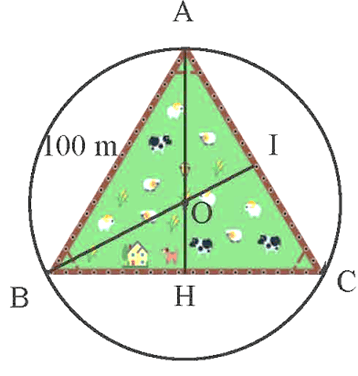
Bài 5 trang 69 Toán 9 Tập 2: Một trại nuôi gia súc có dạng hình tam giác đều cạnh 100 m (Hình 12). Người ta muốn đặt một trụ đèn cao áp tại một điểm cách đều ba đỉnh của tam giác. Nêu cách xác định vị trí đặt đèn và tính khoảng cách từ điểm đó đến ba đỉnh của tam giác.

Lời giải:

Gọi trại có dạng tam giác đều ABC có cạnh bằng 100 m và O là vị trí đặt đèn.

Vì vị trí đặt đèn cách đều ba đỉnh của tam giác nên O là tâm đường tròn ngoại tiếp ∆ABC.

Vẽ hai đường trung tuyến AH và BI, O là giao điểm của AH và BI.

Suy ra O là trọng tâm của ∆ABC.

Áp dụng định lí Pythagore vào tam giác ABH, ta có: AB² = AH² + BH².

Suy ra $AH=\sqrt{A{B}^2-B{H}^2}=\sqrt{{100}^2-{50}^2}=50\sqrt{3}\left(m\right).$ nên $x^2-\frac{x^2}{4}=9$ hay x² = 12.

Do đó R = OA = $\frac{2}{3}$AH = $\frac{2}{3}$.50$\sqrt{3}$ $\approx$ 57,7 (m).

Vậy khoảng cách từ điểm đặt đèn đến ba đỉnh của tam giác khoảng 57,7 m.

Xem thêm Lời giải bài tập Toán 9 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tứ giác nội tiếp

Bài 3: Đa giác đều và phép quay

Bài tập cuối chương 9

Bài 1: Hình trụ

Bài 2: Hình nón