Sách bài tập Toán 10 (Kết nối tri thức) Bài tập cuối chương 2

Giải sách bài tập Toán lớp 10 Bài tập cuối chương 2 - Kết nối tri thức

Giải SBT Toán 10 trang 24 Tập 1

A. Trắc nghiệm

Bài 2.10 trang 24 SBT Toán 10 Tập 1: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. 2x² + 3y > 4.

B. xy + x < 5.

C. 3²x + 4³y ≥ 6.

D. x + y³ ≤ 3.

Lời giải:

Đáp án đúng là: C

Phương án A có x² là hạng tử bậc 2.

Phương án B có xy là hạng tử bậc 2.

Phương án D có y³ là hạng tử bậc 3.

Phương án C có các hạng tử đều có bậc bằng 1.

Vậy ta chọn phương án C.

Bài 2.11 trang 24 SBT Toán 10 Tập 1: Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?

A. $\left\{\begin{array}{l}2\text{x}+3y>4\\ 2^{3}x+3y^2<1\end{array}\right.$.

B. $\left\{\begin{array}{l}x+y>4\\ 2^{3}x+3^{2}y<1\end{array}\right.$.

C. $\left\{\begin{array}{l}x>3\\ y<2\\ x+y\ge y^2\end{array}\right.$.

D. $\left\{\begin{array}{l}x-y\le 3\\ y<1\\ x+y\ge x+xy\end{array}\right.$.

Lời giải:

Đáp án đúng là: B

Phương án A có y² là hạng tử bậc 2.

Phương án C có y² là hạng tử bậc 2.

Phương án D có xy là hạng tử bậc 2.

Phương án B có các hạng tử đều có bậc bằng 1.

Vậy ta chọn phương án B.

Bài 2.12 trang 24 SBT Toán 10 Tập 1: Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + 5y ≤ 10?

A. (5; 2).

B. (-1; 4).

C. (2; 1).

D. (-5; 6).

Lời giải:

Đáp án đúng là: C

Thay x = 4; y = 2 vào biểu thức 2x + 5y ta được 2 . 4 + 5. 2 = 18 > 10 nên phương án A không thỏa mãn.

Thay x = -1; y = 4 vào biểu thức 2x + 5y ta được 2 . (-1) + 5 . 4 = 18 > 10 nên phương án B không thỏa mãn.

Thay x = -5; y = 6 vào biểu thức 2x + 5y ta được 2 . (-5) + 5 . 6 = 20 > 10 nên phương án D không thỏa mãn.

Thay x = 2; y = 1 vào biểu thức 2x + 5y ta được 2 . 2 + 5 . 1 = 9 < 10 nên phương án C đúng.

Vậy ta chọn phương án C.

Bài 2.13 trang 24 SBT Toán 10 Tập 1: Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x - 3y > 13?

A. (1; -5).

B. (2; -4).

C. (3; -3).

D. (8; 1).

Lời giải:

Đáp án đúng là: D

Thay x = 1; y = -5 vào biểu thức 2x - 3y ta được 2 . 1 - 3 . (-5) = 17 > 13 nên phương án A không thỏa mãn.

Thay x = 2; y = -4 vào biểu thức 2x - 3y ta được 2 . 2 - 3 . (-4) = 16 > 13 nên phương án B không thỏa mãn.

Thay x = 3; y = -3 vào biểu thức 2x - 3y ta được 2 . 3 - 3 . (-3) = 15 > 13 nên phương án C không thỏa mãn.

Thay x = 8; y = 1 vào thức 2x - 3y ta được 2 . 8 - 3 . 1 = 13 nên phương án D đúng.

Vậy ta chọn phương án D.

Bài 2.14 trang 24 SBT Toán 10 Tập 1:Cho bất phương trình x + 2y ≤ 3. Khẳng định nào sau đây là đúng?

A. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3 chứa gốc tọa độ.

B. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3 không chứa gốc tọa độ.

C. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = -3 chứa gốc tọa độ.

D. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = -3 không chứa gốc tọa độ.

Lời giải:

Đáp án đúng là: A

Bất phương trình x + 2y ≤ 3 nên miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3.

Do đó đáp án C và D không thỏa mãn.

Thay x = 0; y = 0 vào biểu thức x + 2y ta được 0 + 2 . 0 = 0 < 3.

Suy ra miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3 chứa gốc tọa độ.

Vậy ta chọn phương án A.

Giải SBT Toán 10 trang 25 Tập 1

Bài 2.15 trang 25 SBT Toán 10 Tập 1: Cặp số nào dưới đây là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+y\le 2\\ x-2y\ge 4\\ x>0\end{array}\right.$?

A. (-1; 2).

B. (-2; -4).

C. (0; 1).

D. (2; -4).

Lời giải:

Đáp án đúng là: D

Các phương án A, B, C đều có giá trị x ≤ 0, do đó không thỏa mãn với điều kiện x > 0.

Thay x = 2; y = -4 vào hệ bất phương trình ta có:

x + y = 2 + (-4) = -2 < 2 (thỏa mãn), x - 2y = 2 - 2 . (-4) = 10 > 4 (thỏa mãn), x = 2 > 0 (thỏa mãn).

Vậy chọn phương án D.

Bài 2.16 trang 25 SBT Toán 10 Tập 1: Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+y\le 2\\ x-2y\ge 1\\ y\le 0\end{array}\right.$?

A. (-3; 2).

B. (0; 1).

C. (4; -1).

D. (-2; 2).

Lời giải:

Đáp án đúng là: C

Các phương án A, B, D có giá trị của y > 0 nên không thỏa mãn điều kiện y ≤ 0.

Thay x = 4; y = -1 vào hệ bất phương trình ta được:

-x + y = -4 + (-1) = -5 < 2 (thỏa mãn); x - 2y = 4 - 2 . (-1) = 6 > 1 (thỏa mãn), -1 < 0 (thỏa mãn).

Vậy chọn phương án D.

Bài 2.17 trang 25 SBT Toán 10 Tập 1: Miền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác ABC (miền không bị gạch)?

 

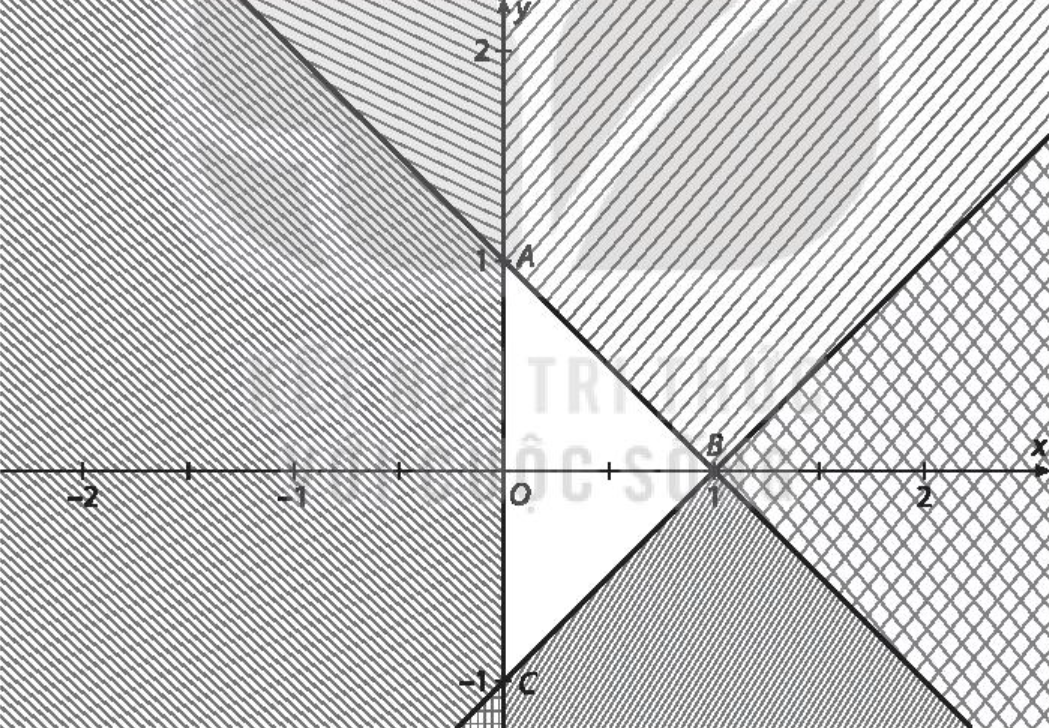
A. $\left\{\begin{array}{l}x+y\le 1\\ x-y\ge 1\\ x\ge 0\end{array}\right.$.

B. $\left\{\begin{array}{l}x+y\le 1\\ x-y\le 1\\ x\ge 0\end{array}\right.$.

C. $\left\{\begin{array}{l}x-y\ge -1\\ x+y\ge -1\\ x\ge 0\end{array}\right.$.

D. $\left\{\begin{array}{l}x-y\ge -1\\ x+y\ge -1\\ y\ge 0\end{array}\right.$.

Lời giải:

Đáp án đúng là: B

Gọi phương trình đường thẳng AB là d₁: y = ax + b.

Do A và B thuộc d₁ nên $\left\{\begin{array}{l}{y}_A=a{x}_A+b\\ y_B=a{x}_B+b\end{array}\right.$ 

$\Rightarrow$ $\left\{\begin{array}{l}1=a.0+b\\ 0=a.1+b\end{array}\right.$

$\Rightarrow$ $\left\{\begin{array}{l}b=1\\ a=-1\end{array}\right.$

Suy ra phương trình đường thẳng AB là y = -x + 1 hay x + y = 1.

Gọi phương trình đường thẳng BC là d₂: y = cx + d.

Do B và C thuộc d₂ nên $\left\{\begin{array}{l}{y}_B=c{x}_B+d\\ y_C=c{x}_C+d\end{array}\right.$ 

$\Rightarrow$ $\left\{\begin{array}{l}0=c.1+d\\ -1=c.0+d\end{array}\right.$

$\Rightarrow$ $\left\{\begin{array}{l}d=-1\\ c=1\end{array}\right.$

Suy ra phương trình đường thẳng BC là y = x - 1 hay x - y = 1.

Đường thẳng AC trùng với trục Oy nên phương trình đường thẳng AC là x = 0.

Ta thấy điểm (0,5; 0) là điểm thuộc miền nghiệm của hệ.

Thay x = 0,5; y = 0 vào biểu thức x + y được 0,5 < 1.

Suy ra bất phương trình thỏa mãn miền nghiệm trên là x + y ≤ 1 (1).

Thay x = 0,5; y = 0 vào biểu thức x - y được 0,5 < 1.

Suy ra bất phương trình thỏa mãn miền nghiệm trên là x - y ≤ 1 (2).

Thay x = 0,5; y = 0 vào biểu thức x được 0,5 > 0.

Suy ra bất phương trình thỏa mãn miền nghiệm trên là x ≥ 0 (3).

Từ (1), (2) và (3) ta có hệ bất phương trình $\left\{\begin{array}{l}x+y\le 1\\ x-y\le 1\\ x\ge 0\end{array}\right.$.

Vậy chọn phương án B.

Giải SBT Toán 10 trang 26 Tập 1

Bài 2.18 trang 26 SBT Toán 10 Tập 1: Miền nghiệm của hệ bất phương trình 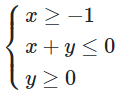 là

A. Một nửa mặt phẳng.

B. Miền tam giác.

C. Miền tứ giác.

D. Miền ngũ giác.

Lời giải:

Đáp án đúng là: B

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Vẽ đường thẳng d₁: x = -1 là một đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng -1.

Chọn điểm I(1; 1) $\in$ d₁ và thay vào biểu thức x ta được 1 > -1.

Suy ra miền nghiệm của bất phương trình x ≥ -1 là nửa mặt phẳng bờ d₁ chứa điểm I(1; 1).

• Vẽ đường thẳng d₂: x + y = 0 bằng cách vẽ một đường thẳng đi qua hai điểm (0; 0) và (-1; 1).

Chọn điểm I(1; 1) $\in$ d₂ và thay vào biểu thức x + y ta được 1 + 1 = 2 > 0.

Suy ra miền nghiệm của bất phương trình x + y ≤ 0 là nửa mặt phẳng bờ d₂ không chứa điểm I(1; 1).

• Đường thẳng d₃: y = 0 trùng với trục Ox.

Chọn điểm I(1; 1) $\in$ d₃ và thay vào biểu thức y ta được 1 > 0.

Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d₃ chứa điểm I(1; 1).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

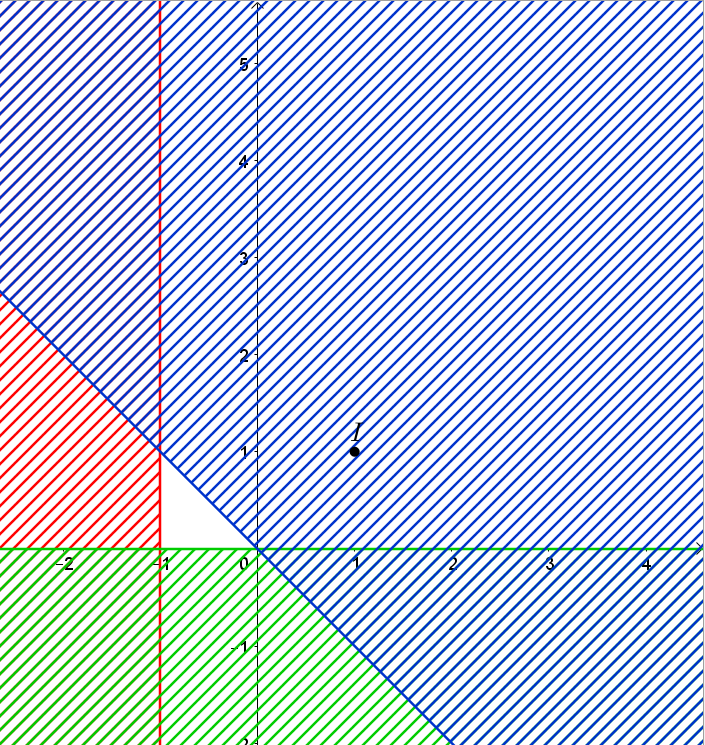
Ta thấy miền nghiệm của hệ bất phương trình trên là miền tam giác.

Vậy chọn phương án B.

Bài 2.19 trang 26 SBT Toán 10 Tập 1: Miền nghiệm của bất phương trình $\left\{\begin{array}{l}x+y\le 1\\ -3\le y\le 3\\ -3\le x\le 3\end{array}\right.$ là

A. Miền lục giác.

B. Miền tam giác.

C. Miền tứ giác.

D. Miền ngũ giác.

Lời giải:

Đáp án đúng là: D

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Vẽ đường thẳng d₁: x + y = 1 bằng cách vẽ đường thẳng đi qua hai điểm (0; 1) và (1; 0).

Chọn điểm O(0; 0) $\in$ d₁ và thay vào biểu thức x + y được 0 < 1.

Suy ra miền nghiệm của bất phương trình x + y ≤ 1 là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0).

• Đường thẳng d₂: y = -3 là đường thẳng song song với trục Ox và đi qua điểm có hoành độ bằng -3.

Chọn điểm O(0; 0) $\in$ d₂ và thay vào biểu thức y được 0 > -3.

Suy ra miền nghiệm của bất phương trình y ≥ -3 là nửa mặt phẳng bờ d₂ chứa điểm O(0; 0).

• Đường thẳng d₃: y = 3 là đường thẳng song song với trục Ox và đi qua điểm có hoành độ bằng 3.

Chọn điểm O(0; 0) và thay vào biểu thức y được 0 < 3.

Suy ra miền nghiệm của bất phương trình y ≤ 3 là nửa mặt phẳng bờ d₃ chứa điểm O(0; 0).

• Đường thẳng d₄: x = -3 là đường thẳng song song với trục Oy và đi qua điểm có tung độ bằng -3.

Chọn điểm O(0; 0) $\in$ d₄ và thay vào biểu thức x được 0 > -3.

Suy ra miền nghiệm của bất phương trình x ≥ -3 là nửa mặt phẳng bờ d₄ chứa điểm O(0; 0).

• Đường thẳng d₅: x = 3 là đường thẳng song song với trục Oy và đi qua điểm có tung độ bằng 3.

Chọn điểm O(0; 0) và thay vào biểu thức x được 0 < 3.

Suy ra miền nghiệm của bất phương trình x ≤ 3 là nửa mặt phẳng bờ d₅ chứa điểm O(0; 0).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

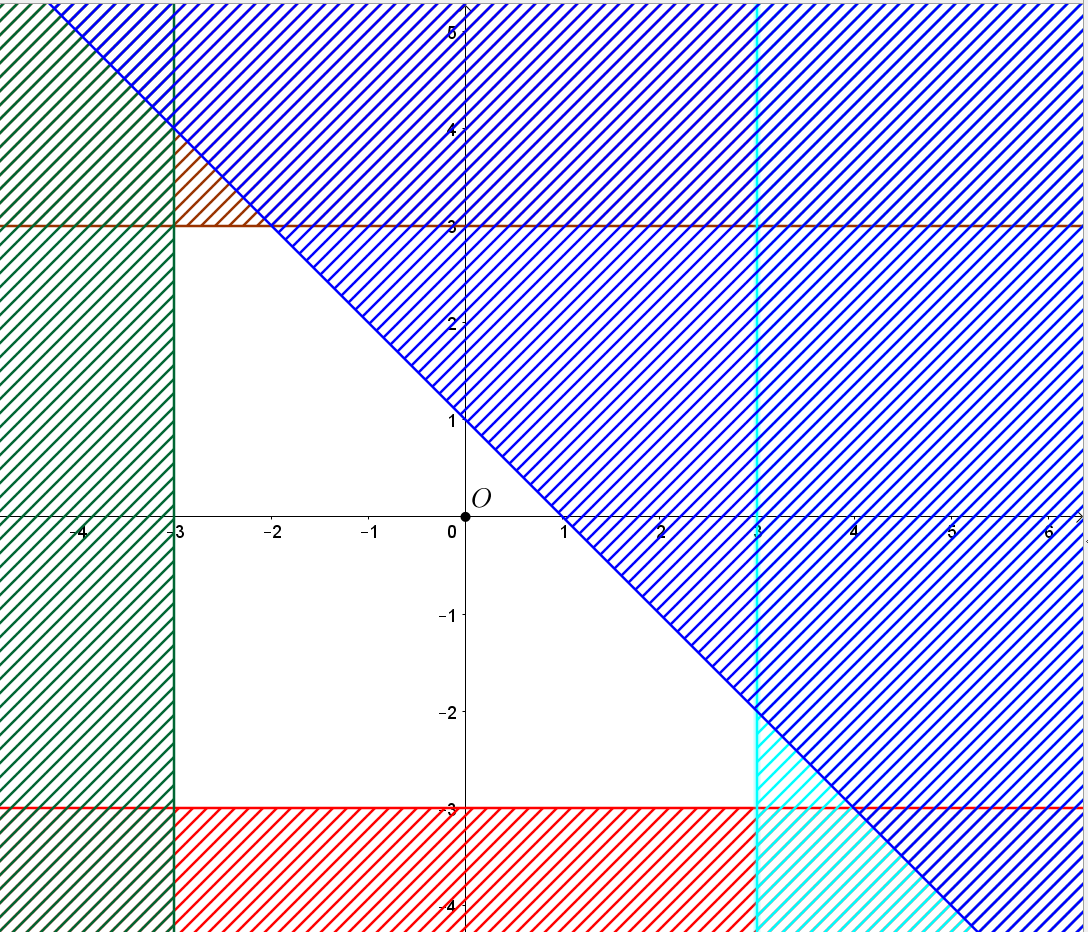
Ta thấy miền nghiệm của hệ là miền ngũ giác.

Vậy chọn phương án D.

Bài 2.20 trang 26 SBT Toán 10 Tập 1: Miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+y\le 10\\ -3\le y\le 3\\ -3\le x\le 3\end{array}\right.$ là

A. Miền lục giác.

B. Miền tam giác.

C. Miền tứ giác.

D. Miền ngũ giác.

Lời giải:

Đáp án đúng là: C

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Vẽ đường thẳng d₁: x + y = 10 bằng cách vẽ đường thẳng đi qua hai điểm (4; 6) và (5; 5).

Chọn điểm O(0; 0) $\in$ d₁ và thay vào biểu thức x + y được 0 < 10.

Suy ra miền nghiệm của bất phương trình x + y ≤ 10 là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0).

• Đường thẳng d₂: y = -3 là đường thẳng song song với trục Ox và đi qua điểm có hoành độ bằng -3.

Chọn điểm O(0; 0) $\in$ d₂ và thay vào biểu thức y được 0 > -3.

Suy ra miền nghiệm của bất phương trình y ≥ -3 là nửa mặt phẳng bờ d₂ chứa điểm O(0; 0).

• Đường thẳng d₃: y = 3 là đường thẳng song song với trục Ox và đi qua điểm có hoành độ bằng 3.

Chọn điểm O(0; 0) và thay vào biểu thức y được 0 < 3.

Suy ra miền nghiệm của bất phương trình y ≤ 3 là nửa mặt phẳng bờ d₃ chứa điểm O(0; 0).

• Đường thẳng d₄: x = -3 là đường thẳng song song với trục Oy và đi qua điểm có tung độ bằng -3.

Chọn điểm O(0; 0) $\in$ d₄ và thay vào biểu thức x được 0 > -3.

Suy ra miền nghiệm của bất phương trình x ≥ -3 là nửa mặt phẳng bờ d₄ chứa điểm O(0; 0).

• Đường thẳng d₅: x = 3 là đường thẳng song song với trục Oy và đi qua điểm có tung độ bằng 3.

Chọn điểm O(0; 0) và thay vào biểu thức x được 0 < 3.

Suy ra miền nghiệm của bất phương trình x ≤ 3 là nửa mặt phẳng bờ d₅ chứa điểm O(0; 0).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

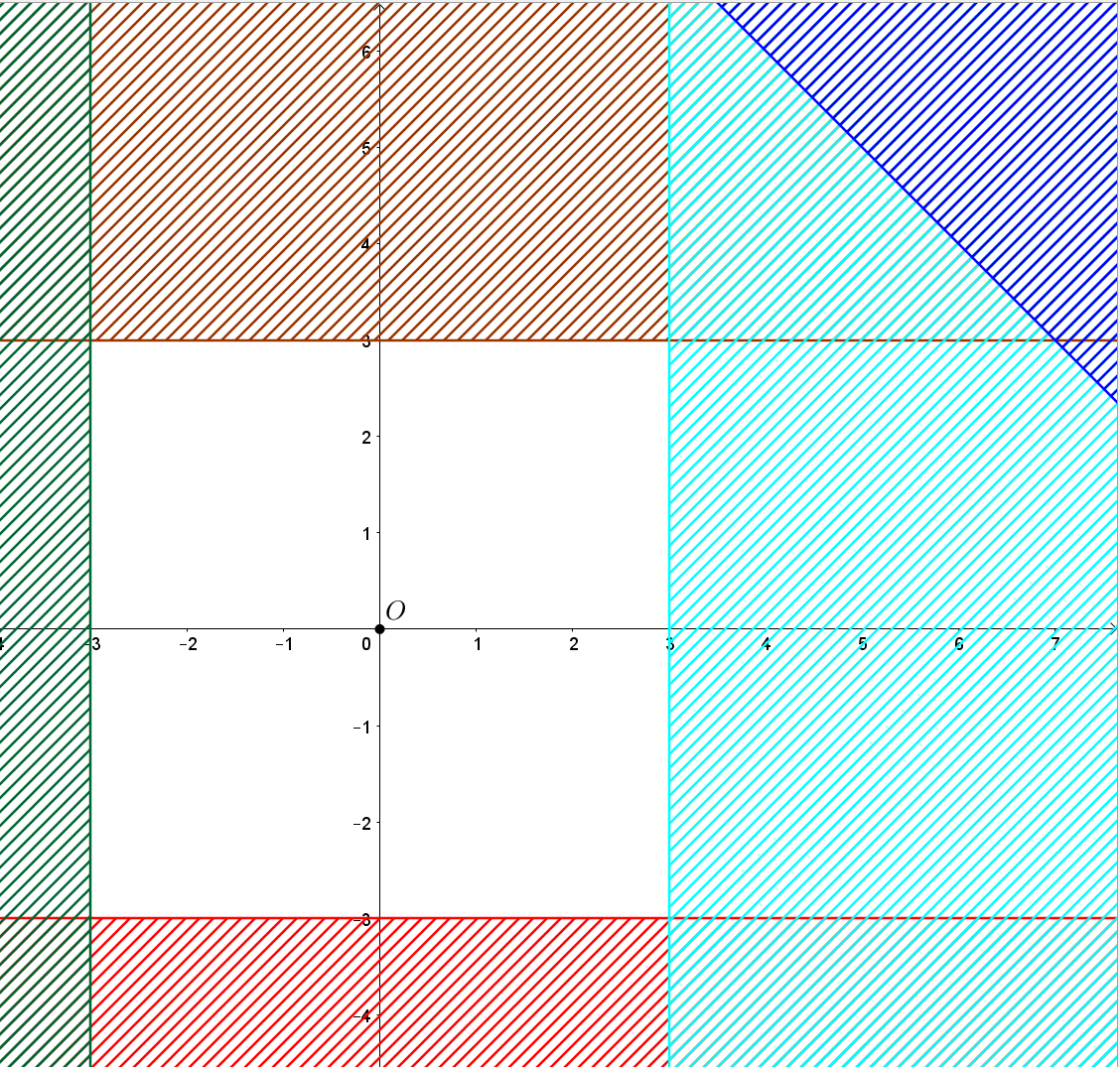
Ta thấy miền nghiệm của hệ là miền tứ giác.

Vậy chọn đáp án C.

Bài 2.21 trang 26 SBT Toán 10 Tập 1: Giá trị lớn nhất của biểu thức F(x; y) = 3x + y với (x; y) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x\ge -1\\ x+y\le 2\\ y\ge 0\end{array}\right.$ là

A. -3.

B. 6.

C. 5.

D. 8.

Lời giải:

Đáp án đúng là: B

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: x = -1 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng -1.

Chọn điểm I(0; 1) $\in$ d₁ và thay vào biểu thức x được 0 > -1.

Suy ra miền nghiệm của bất phương trình x ≥ -1 là nửa mặt phẳng bờ d₁ chứa điểm I(0; 1).

• Vẽ đường thẳng d₂: x + y = 2 bằng cách vẽ một đường thẳng đi qua hai điểm (0; 2) và (2; 0).

Chọn điểm I(0; 1) $\in$ d₂ và thay vào biểu thức x + y được 1 < 2.

Suy ra miền nghiệm của bất phương trình x + y ≤ 2 là nửa mặt phẳng bờ d₂ chứa điểm I(0; 1).

• Đường thẳng d₃: y = 0 là đường thẳng trùng với trục Ox.

Chọn điểm I(0; 1) $\in$ d₃ và thay vào biểu thức y được 1 > 0.

Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d₃ chứa điểm I(0; 1).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

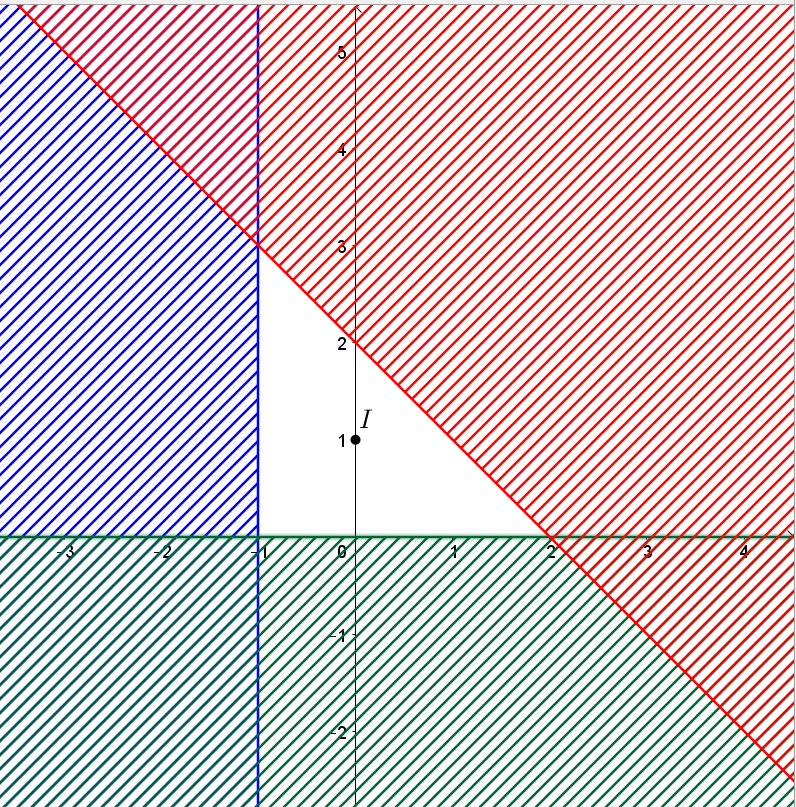
Miền nghiệm của hệ bất phương trình là miền tam giác với các đỉnh (-1; 3), (-1; 0) và (2; 0).

Ta có F(-1; 3) = 3 . (-1) + 3 = 0;

F(-1; 0) = 3 . (-1) + 0 = -3;

F(2; 0) = 3 . 2 + 0 = 6.

Do đó giá trị F(x; y) lớn nhất bằng 6 với x = 2; y = 0.

Vậy chọn phương án B.

Bài 2.22 trang 26 SBT Toán 10 Tập 1: Giá trị nhỏ nhất của biểu thức F(x; y) = -x + 4y với (x; y) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x\ge 1\\ x\le 2\\ y\ge 0\\ y\le 3\end{array}\right.$ là

A. -2.

B. 3.

C. 11.

D. -4.

Lời giải:

Đáp án đúng là: A

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: x = 1 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 1.

Chọn điểm I(1,5; 1) $\in$ d₁ và thay vào biểu thức x ta được 1,5 > 1.

Suy ra miền nghiệm của bất phương trình x ≥ 1 là nửa mặt phẳng bờ d₁ có chứa điểm I(1,5; 1).

• Đường thẳng d₂: x = 2 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 2.

Chọn điểm I(1,5; 1) $\in$ d₂ và thay vào biểu thức x ta được 1,5 < 2.

Suy ra miền nghiệm của bất phương trình x ≤ 2 là nửa mặt phẳng bờ d₂ có chứa điểm I(1,5; 1).

• Đường thẳng d₃: y = 0 là đường thẳng trùng với trục Ox.

Chọn điểm I(1,5; 1) $\in$ d₃ và thay vào biểu thức y ta được 1 > 0.

Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d₃ có chứa điểm I(1,5; 1).

• Đường thẳng d₄: y = 3 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 3.

Chọn điểm I(1,5; 1) $\in$ d₃ và thay vào biểu thức y ta được 1 < 3.

Suy ra miền nghiệm của bất phương trình y ≤ 3 là nửa mặt phẳng bờ d₄ có chứa điểm I(1,5; 1).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

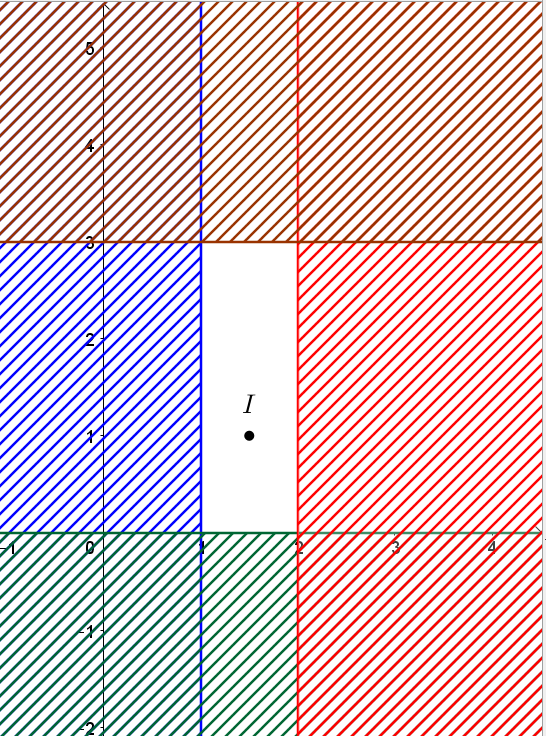
Miền nghiệm của hệ bất phương trình trên là miền tứ giác với các đỉnh (1; 0), (1; 3), (2; 3) và (2; 0).

Ta có:

F(1; 0) = -1 + 4 . 0 = -1;

F(1; 3) = -1 + 4 . 3 = 11;

F(2; 3) = -2 + 4 . 3 = 10;

F(2; 0) = -2 + 4 . 0 = -2.

Do đó giá trị F(x; y) nhỏ nhất bằng -2 khi x = 2; y = 0.

Vậy chọn phương án A.

Bài 2.23 trang 26 SBT Toán 10 Tập 1: Tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = x + 5y với (x; y) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-2\le y\le 2\\ x+y\le 4\\ y-x\le 4\end{array}\right.$ là

A. -20.

B. -4.

C. 28.

D. 16.

Lời giải:

Đáp án đúng là: B

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: y = -2 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng -2.

Chọn điểm O(0; 0) $\in$ d₁ và thay vào biểu thức y được 0 > -2.

Suy ra miền nghiệm của bất phương trình -2 ≤ y là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0).

• Đường thẳng d₂: y = 2 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 2.

Chọn điểm O(0; 0) $\in$ d₂ và thay vào biểu thức y được 0 < 2.

Suy ra miền nghiệm của bất phương trình y ≤ 2 là nửa mặt phẳng bờ d₂ chứa điểm O(0; 0).

• Vẽ đường thẳng d₃: x + y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (4; 0).

Chọn điểm O(0; 0) $\in$ d₃ và thay vào biểu thức x + y được 0 < 4.

Suy ra miền nghiệm của bất phương trình x + y ≤ 4 là nửa mặt phẳng bờ d₃ chứa điểm O(0; 0).

• Vẽ đường thẳng d₄: y - x = 4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (1; 5).

Chọn điểm O(0; 0) $\in$ d₄ và thay vào biểu thức y - x được 0 < 4.

Suy ra miền nghiệm của bất phương trình y - x ≤ 4 là nửa mặt phẳng bờ d₄ chứa điểm O(0; 0).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

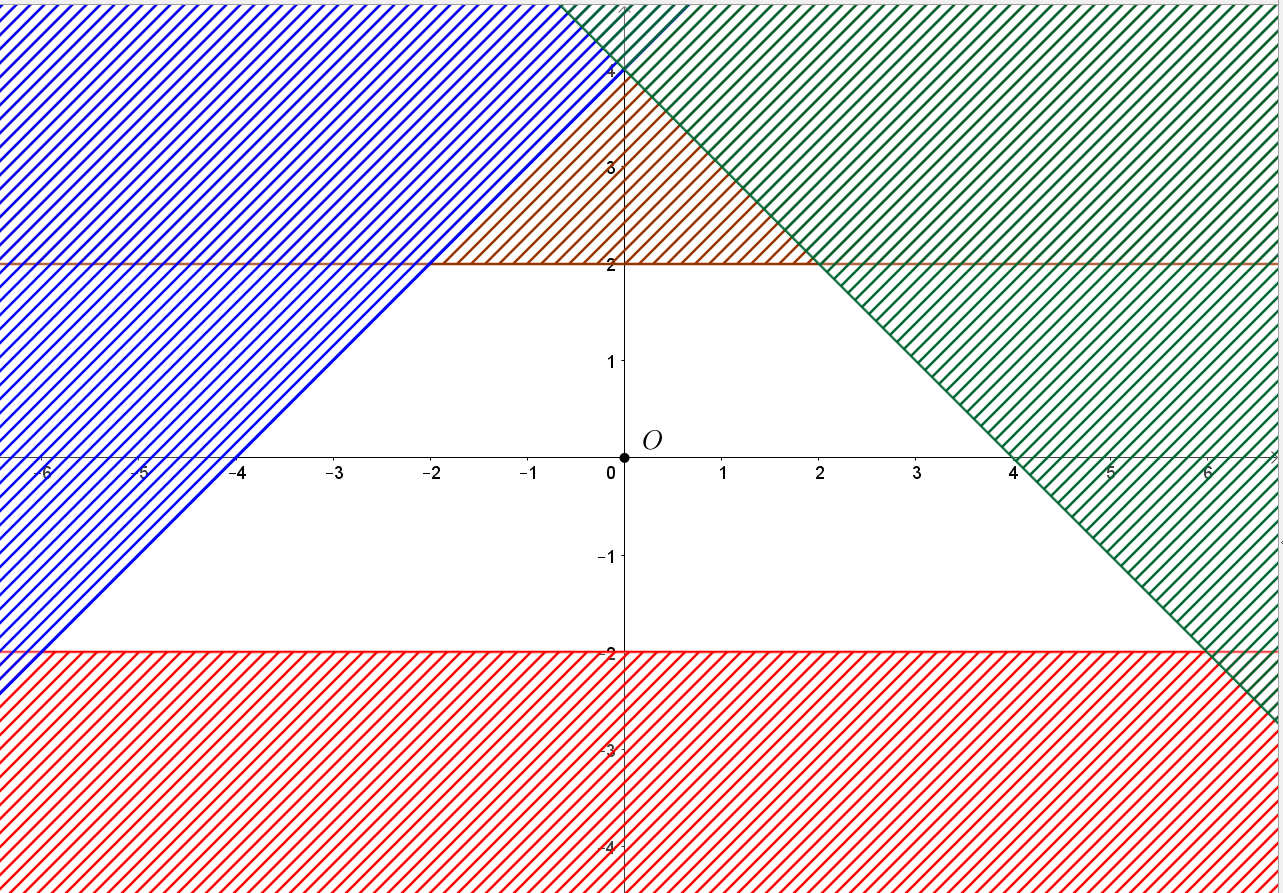
Ta thấy miền nghiệm của hệ bất phương trình trên là miền tứ giác với các đỉnh (-6; -2), (-2; 2), (2;2) và (6; -2).

Ta có:

F(-6; -2) = -6 + 5 . (-2) = -16;

F(-2; 2) = -2 + 5 . 2 = 8;

F(2; 2) = 2 + 5 . 2 = 12;

F(6; -2) = 6 + 5 . (-2) = -4.

Do đó giá trị lớn nhất của F(x; y) = 12 và giá trị nhỏ nhất của F(x; y) = -16.

Suy ra tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) với (x; y) thuộc miền nghiệm của hệ bất phương trình trên là 12 + (-16) = -4.

Vậy chọn phương án B.

Giải SBT Toán 10 trang 27, 28 Tập 1

Bài 2.24 trang 27 SBT Toán 10 Tập 1: Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc X và Y để tạo thành thức ăn hỗn hợp cho gia súc. Giá một bao loại X là 250 nghìn đồng, giá một bao loại Y là 200 nghìn đồng. Mỗi bao loại X chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C. Mỗi bao loại Y chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C. Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc X và Y sao cho hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C.

A. 1,95 triệu đồng.

B. 4,5 triệu đồng.

C. 1,85 triệu đồng.

D. 1,7 triệu đồng.

Lời giải:

Đáp án đúng là: A

Gọi số bao loại X và số bao loại Y lần lượt là x bao và y bao (x, y $\in$ ℕ).

Mỗi bao loại X chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C nên x bao loại X chứa 2x đơn vị chất dinh dưỡng A, 2x đơn vị chất dinh dưỡng B và 2x đơn vị chất dinh dưỡng C.

Mỗi bao loại Y chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C nên y bao loại Y chứa y đơn vị chất dinh dưỡng A, 9y đơn vị chất dinh dưỡng B và 3y đơn vị chất dinh dưỡng C.

Hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C nên 2x + y ≥ 12; 2x + 9y ≥ 36; 2x + 3y ≥ 24.

Khi đó ta có hệ bất phương trình sau $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 2x+y\ge 12\\ 2\text{x}+9y\ge 36\\ 2\text{x}+3y\ge 24\end{array}\right.$

F(x; y) = 250x + 200y (triệu đồng).

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: x = 0 là đường thẳng trùng với trục Oy.

Chọn điểm I(5; 5) $\in$ d₁ và thay vào biểu thức x ta được 5 > 0.

Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d₁ chứa điểm I(5; 5).

• Đường thẳng d₂: y = 0 là đường thẳng trùng với trục Ox.

Chọn điểm I(5; 5) $\in$ d₂ và thay vào biểu thức y ta được 5 > 0.

Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d₂ chứa điểm I(5; 5).

• Vẽ đường thẳng d₃: 2x + y = 12 bằng cách vẽ đường thẳng đi qua hai điểm (6; 0) và (5; 2).

Chọn điểm I(5; 5) $\in$ d₃ và thay vào biểu thức 2x + y ta được 2 . 5 + 5 = 15 > 12.

Suy ra miền nghiệm của bất phương trình 2x + y ≥ 12 là nửa mặt phẳng bờ d₃ chứa điểm I(5; 5).

• Vẽ đường thẳng d₄: 2x + 9y = 36 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (4,5; 3).

Chọn điểm I(5; 5) $\in$ d₄ và thay vào biểu thức 2x + 9y ta được 2 . 5 + 9 . 5 = 55 > 36.

Suy ra miền nghiệm của bất phương trình 2x + 9y ≥ 36 là nửa mặt phẳng bờ d₄ chứa điểm I(5; 5).

• Vẽ đường thẳng d₅: 2x + 3y = 24 bằng cách vẽ đường thẳng đi qua hai điểm (3; 6) và (6; 4).

Chọn điểm I(5; 5) $\in$ d₅ và thay vào biểu thức 2x + 3y ta được 2 . 5 + 3 . 5 = 25 > 24.

Suy ra miền nghiệm của bất phương trình 2x + 3y ≥ 24 là nửa mặt phẳng bờ d₅ chứa điểm I(5; 5).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

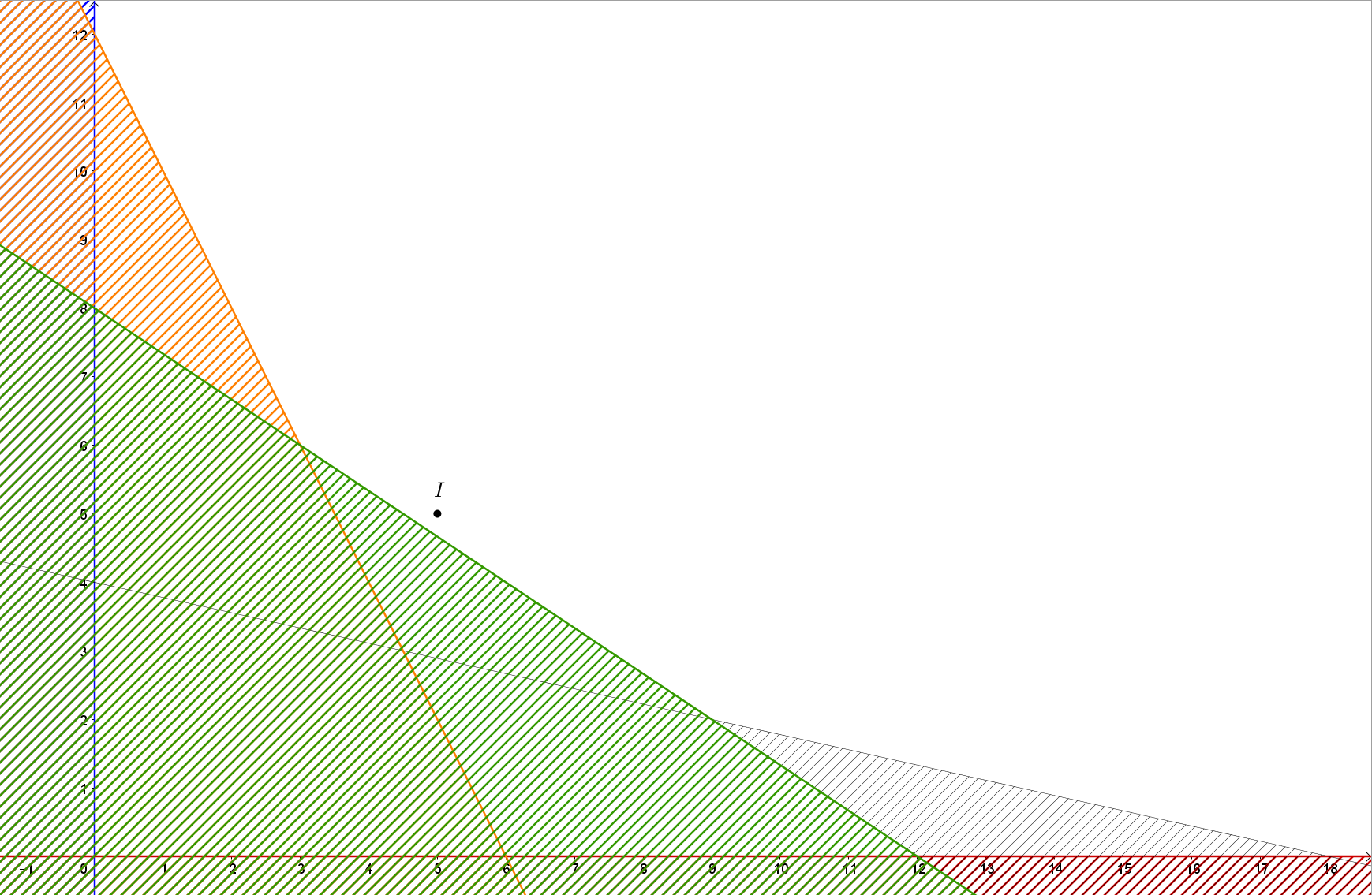
Miền nghiệm của hệ được giới hạn bởi các điểm (0; 12); (3; 6); (9; 2); (18; 0).

Ta có:

F(0; 12) = 250 . 0 + 200 . 12 = 2 400;

F(3; 6) = 250 . 3 + 200 . 6 = 1 950;

F(9; 2) = 250 . 9 + 200 . 2 = 2 650;

F(18; 0) = 250 . 18 + 200 . 0 = 4 500.

Khi đó ta thấy F(x; y) đạt giá trị nhỏ nhất bằng 1 950 tại x = 3; y = 6.

Vậy chi phí nhỏ nhất để mua hai loại thức ăn là 1,95 triệu đồng.

B. Tự luận

Bài 2.25 trang 27 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của các bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:

a) x + y ≥ -4;

b) 2x - y ≤ 5;

c) x + 2y < 0;

d) -x + 2y > 0.

Lời giải:

a) Biểu diễn tập nghiệm của bất phương trình x + y ≥ -4 trên mặt phẳng tọa độ:

• Vẽ đường thẳng d₁: x + y = -4 bằng cách vẽ đường thẳng đi qua hai điểm (0; -4) và (-4; 0).

• Chọn điểm O(0; 0) $\in$ d₁ và thay vào biểu thức x + y ta được 0 > -4.

Suy ra miền nghiệm của bất phương trình x + y ≥ -4 là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0).

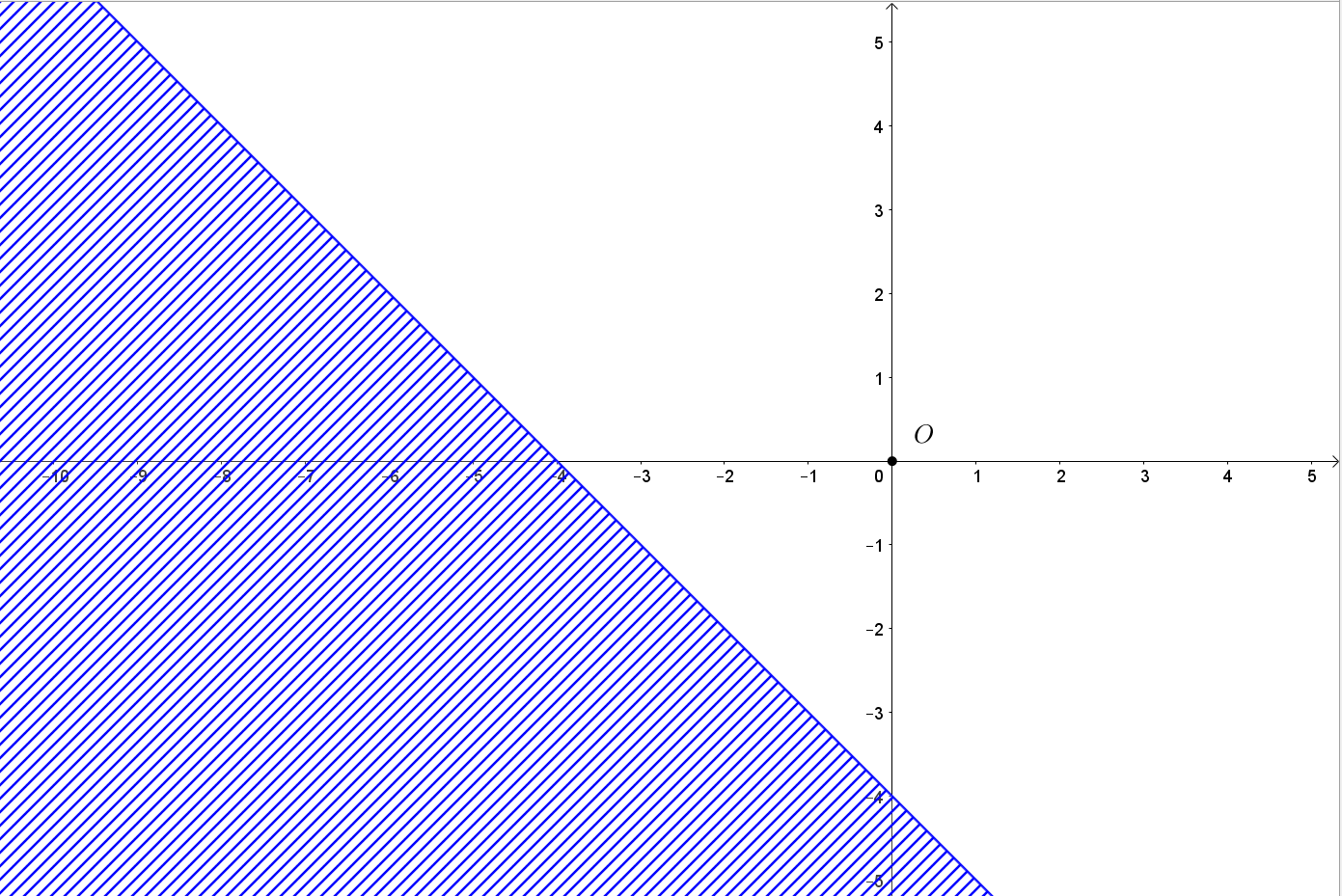
b) Biểu diễn tập nghiệm của bất phương trình 2x - y ≤ 5 trên mặt phẳng tọa độ:

• Vẽ đường thẳng d₁: 2x - y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; -5) và (3; 1).

• Chọn điểm O(0; 0) $\in$ d₁ và thay vào biểu thức 2x - y ta được 0 < 5.

Suy ra miền nghiệm của bất phương trình 2x - y ≤ 5 là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0).

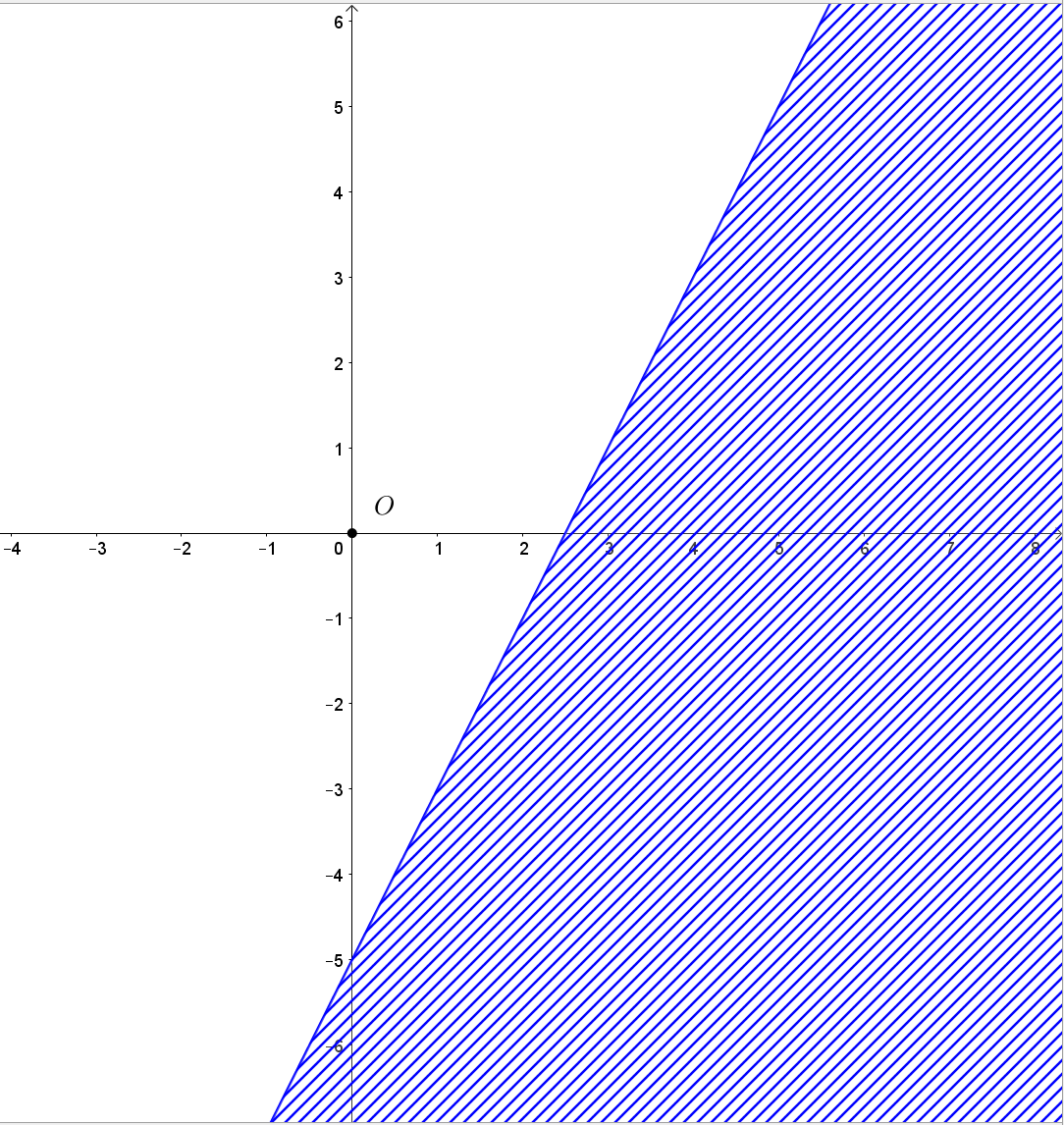
c) Biểu diễn tập nghiệm của bất phương trình x + 2y < 0 trên mặt phẳng tọa độ:

• Vẽ đường thẳng d₁: x + 2y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (2; -1).

Chọn điểm I(1; 1) $\in$ d₁ và thay vào biểu thức x + 2y ta được 1 + 2 . 1 = 3 > 0.

• Suy ra miền nghiệm của bất phương trình x + 2y < 0 là nửa mặt phẳng bờ d₁ không chứa điểm I(1; 1) và bỏ đi đường thẳng d₁.

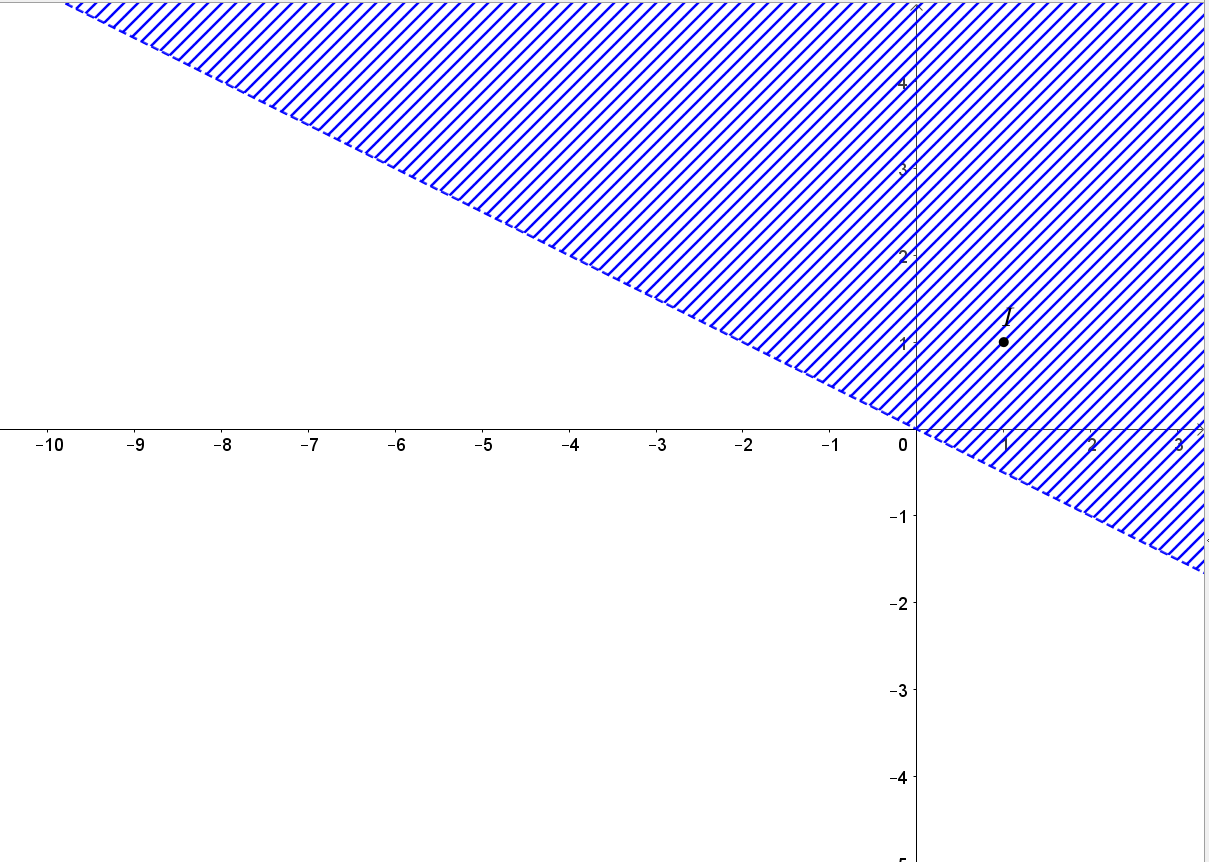
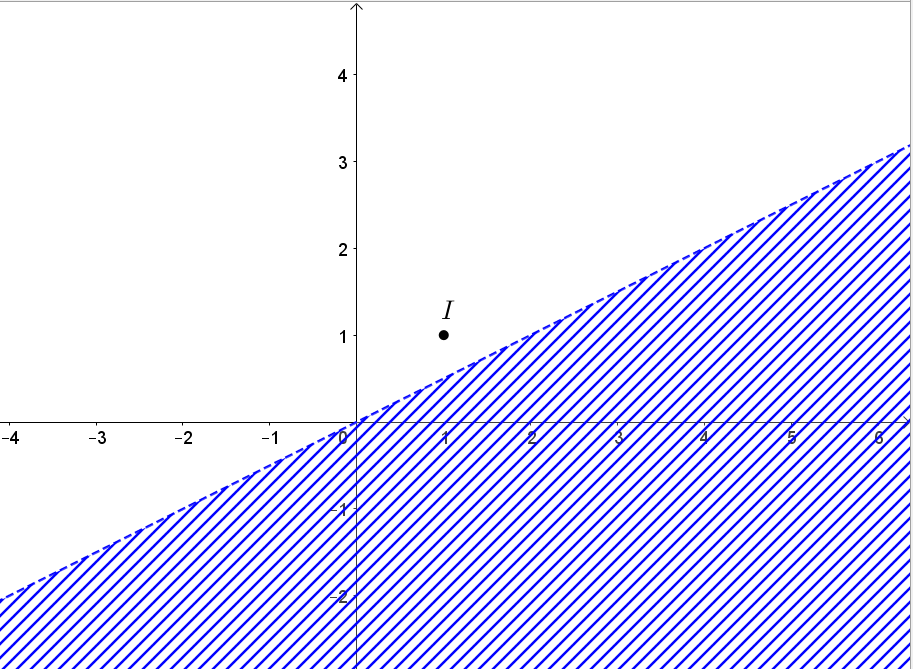
d) Biểu diễn tập nghiệm của bất phương trình -x + 2y > 0 trên mặt phẳng tọa độ:

• Vẽ đường thẳng d₁: -x + 2y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (2; 1).

• Chọn điểm I(1; 1) $\in$ d₁ và thay vào biểu thức -x + 2y ta được 1 > 0.

Suy ra miền nghiệm của bất phương trình -x + 2y > 0 là nửa mặt phẳng bờ d₁ chứa điểm I(1; 1) và bỏ đi đường thẳng d₁.

Bài 2.26 trang 27 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:

a) $\left\{\begin{array}{l}0\le x\le 10\\ y>0\\ x-y>4\end{array}\right.$;

b) $\left\{\begin{array}{l}0\le y\le 1\\ x+y\le 2\\ y-x\le 2\end{array}\right.$;

c) $\left\{\begin{array}{l}x\ge 0\\ 4\text{x}-6y<0\\ 2\text{x}-3y\ge 1\end{array}\right.$.

Lời giải:

a) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: x = 0 là đường thẳng trùng với trục Oy.

Chọn điểm I(1; 1) $\in$ d₁ và thay vào biểu thức x ta được 1 > 0.

Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d₁ chứa điểm I(1; 1).

• Đường thẳng d₂: x = 10 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 10.

Chọn điểm I(1; 1) $\in$ d₂ và thay vào biểu thức x ta được 1 < 10.

Suy ra miền nghiệm của bất phương trình x ≤ 10 là nửa mặt phẳng bờ d₂ chứa điểm I(1; 1).

• Đường thẳng d₃: y = 0 là đường thẳng trùng với trục Ox.

Chọn điểm I(1; 1) $\in$ d₃ và thay vào biểu thức y ta được 1 > 0.

Suy ra miền nghiệm của bất phương trình y > 0 là nửa mặt phẳng bờ d₃ chứa điểm I(1; 1) và bỏ đi đường thẳng d₃.

• Vẽ đường thẳng d₄: x - y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (4; 0) và (0; -4).

Chọn điểm I(1; 1) $\in$ d₄ và thay vào biểu thức x - y ta được 0 < 4.

Suy ra miền nghiệm của bất phương trình x - y > 4 là nửa mặt phẳng bờ d₄ không chứa điểm I(1; 1) và bỏ đi đường thẳng d₄.

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

b) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: y = 0 là đường thẳng trùng với trục Ox.

Chọn điểm I(0; 0,5) $\in$ d₁ và thay vào biểu thức y ta được 0,5 > 0.

Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d₁ chứa điểm I(0; 0,5).

• Đường thẳng d₂: y = 1 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 1.

Chọn điểm I(0; 0,5) $\in$ d₂ và thay vào biểu thức y ta được 0,5 < 1.

Suy ra miền nghiệm của bất phương trình y ≤ 1 là nửa mặt phẳng bờ d₂ chứa điểm I(0; 0,5).

• Vẽ đường thẳng d₃: x + y = 2 bằng cách vẽ đường thẳng đi qua hai điểm (2; 0) và (0; 2).

Chọn điểm I(0; 0,5) $\in$ d₃ và thay vào biểu thức x + y ta được 0,5 < 2.

Suy ra miền nghiệm của bất phương trình x + y ≤ 2 là nửa mặt phẳng bờ d₃ chứa điểm I(0; 0,5).

• Vẽ đường thẳng d₄: y - x = 2 bằng cách vẽ đường thẳng đi qua hai điểm (0; 2) và (-2; 0).

Chọn điểm I(0; 0,5) $\in$ d₄ và thay vào biểu thức y - x ta được 0,5 < 2.

Suy ra miền nghiệm của bất phương trình y - x ≤ 2 là nửa mặt phẳng bờ d₄ chứa điểm I(0; 0,5).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

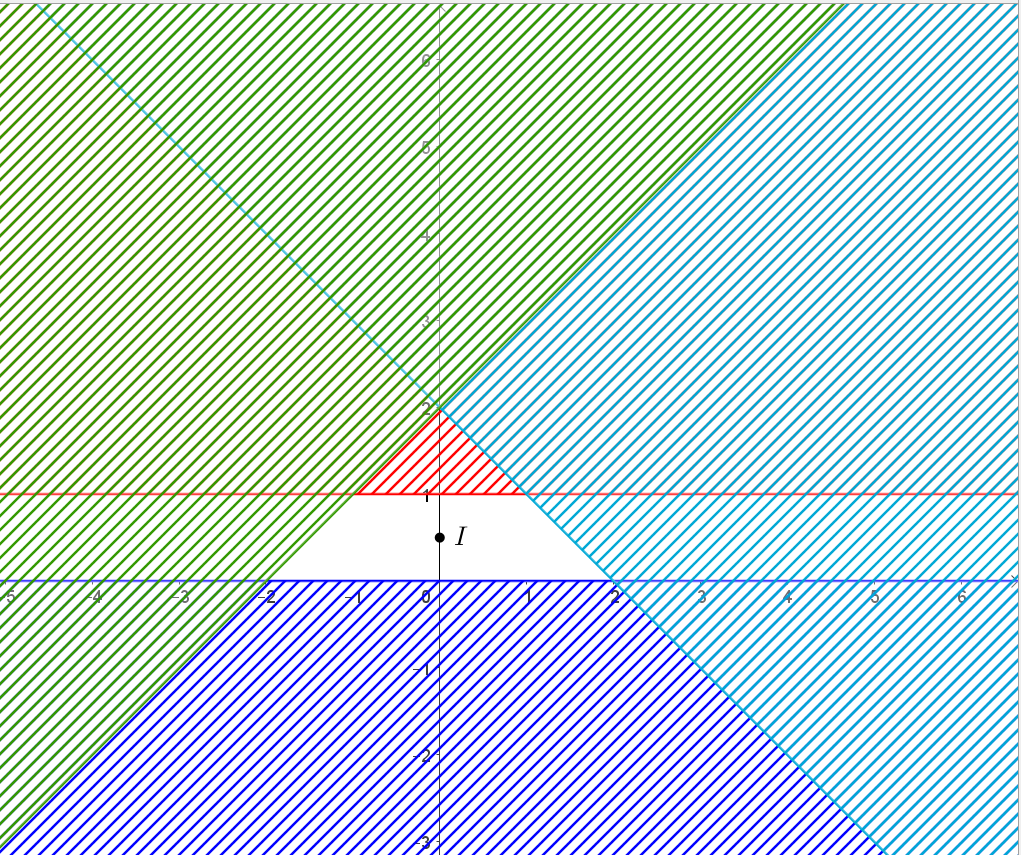
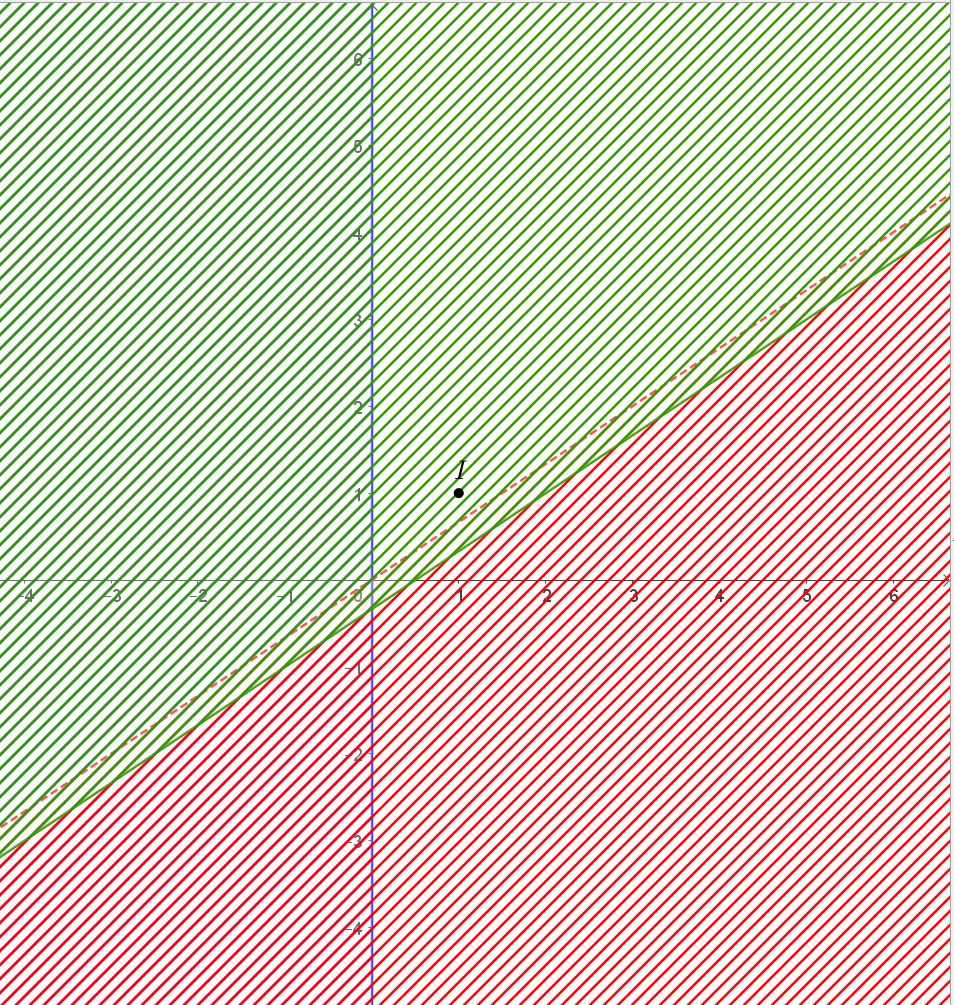
c) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: x = 0 là đường thẳng trùng với trục Oy.

Chọn điểm I(1; 1) $\in$ d₁ và thay vào biểu thức x ta được 1 > 0.

Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d₁ chứa điểm I(1; 1).

• Vẽ đường thẳng d₂: 4x - 6y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (3; 2).

Chọn điểm I(1; 1) $\in$ d₂ và thay vào biểu thức 4x - 6y ta được -2 < 0.

Suy ra miền nghiệm của bất phương trình 4x - 6y < 0 là nửa mặt phẳng bờ d₂ chứa điểm I(1; 1) và bỏ đi đường thẳng d₂.

• Vẽ đường thẳng d₃: 2x - 3y = 1 bằng cách vẽ đường thẳng đi qua hai điểm (2; 1) và (5; 3).

 Chọn điểm I(1; 1) $\in$ d₃ và thay vào biểu thức 2x - 3y ta được -1 < 1.

Suy ra miền nghiệm của bất phương trình 2x - 3y ≥ 1 là nửa mặt phẳng bờ d₃ không chứa điểm I(1; 1).

Khi đó hệ vô nghiệm vì mặt phẳng tọa độ đều bị gạch.

Bài 2.27 trang 27 SBT Toán 10 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y với (x; y) thuộc miền nghiệm của hệ bất phương trình

 $\left\{\begin{array}{l}y\ge -1\\ y\le 1\\ x+y\le 4\\ y-x\le 4\end{array}\right.$.

Lời giải:

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: y = -1 là đường thẳng song song với trục Ox đi qua điểm có tung độ bằng -1.

Chọn điểm O(0; 0) $\in$ d₁ và thay vào biểu thức y ta được 0 > -1.

Suy ra miền nghiệm của bất phương trình y ≥ -1 là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0).

• Đường thẳng d₂: y = 1 là đường thẳng song song với trục Ox đi qua điểm có tung độ bằng 1.

Chọn điểm O(0; 0) $\in$ d₂ và thay vào biểu thức y ta được 0 < 1.

Suy ra miền nghiệm của bất phương trình y ≤ 1 là nửa mặt phẳng bờ d₂ chứa điểm O(0; 0).

• Vẽ đường thẳng d₃: x + y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (4; 0).

Chọn điểm O(0; 0) $\in$ d₃ và thay vào biểu thức x + y ta được 0 < 4.

Suy ra miền nghiệm của bất phương trình x + y ≤ 4 là nửa mặt phẳng bờ d₃ chứa điểm O(0; 0).

• Vẽ đường thẳng d₄: y - x = 4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (-4; 0).

Chọn điểm O(0; 0) $\in$ d₄ và thay vào biểu thức y - x ta được 0 < 4.

Suy ra miền nghiệm của bất phương trình y - x ≤ 4 là nửa mặt phẳng bờ d₄ chứa điểm O(0; 0).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

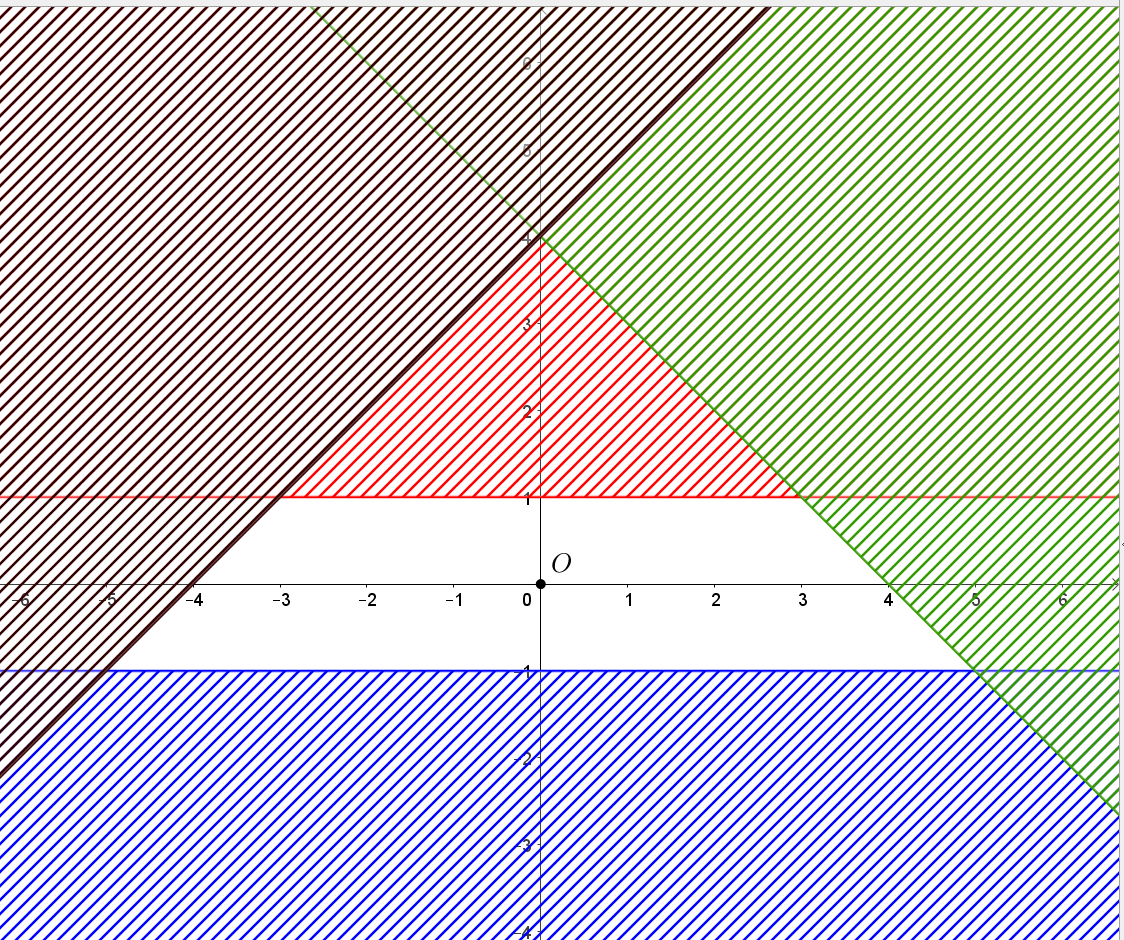
Ta thấy miền nghiệm của hệ bất phương trình trên là miền tứ giác với các đỉnh (-5; -1), (-3; 1), (3; 1), (5; -1).

Ta có:

F(-5; -1) = 2 . (-5) + 3 . (-1) = -13;

F(-3; 1) = 2 . (-3) + 3 . 1 = -3;

F(3; 1) = 2 . 3 + 3 . 1 = 9;

F(5; -1) = 2 . 5 + 3 . (-1) = 7.

Khi đó giá trị nhỏ nhất của F(x; y) là F(-5; -1) = -13 và giá trị lớn nhất là F(3; 1) = 9.

Bài 2.28 trang 27 SBT Toán 10 Tập 1: Một phân xưởng có hai máy chuyên dụng M1 và M2 để sản xuất hai loại sản phẩm A và B theo đơn đặt hàng. Nếu sản xuất được một tấn sản phẩm loại A thì phân xưởng nhận được số tiền lãi là 2 triệu đồng. Nếu sản xuất được một tấn sản phẩm loại B thì phân xưởng nhận được số tiền lãi là 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A, người ta phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B, người ta phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm này. Máy M1 làm việc không quá 6 giờ một ngày và máy M2 làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu?

Lời giải:

Gọi số sản phẩm loại A và loại B sản xuất ra lần lượt là x tấn và y tấn (x, y ≥ 0).

Để sản xuất x tấn sản phẩm loại A thì máy M₁ cần hoạt động trong 3x giờ, máy M₂ cần hoạt động trong x giờ.

Để sản xuất y tấn sản phẩm loại B thì máy M₁ cần hoạt động y giờ, máy M₂ cần hoạt động trong y giờ.

Do máy M₁ làm việc không quá 6 giờ một ngày và máy M₂ làm việc không quá 4 giờ một ngày nên 3x + y ≤ 6; x + y ≤ 4.

Khi đó ta có hệ phương trình $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 3\text{x}+y\le 6\\ x+y\le 4\end{array}\right.$

F(x; y) = 2x + 1,6y (triệu đồng).

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: x = 0 là đường thẳng trùng với trục Oy.

Chọn điểm I(1; 1) $\in$ d₁ và thay vào biểu thức x ta được 1 > 0.

Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d₁ chứa điểm I(1; 1).

• Đường thẳng d₂: y = 0 là đường thẳng trùng với trục Ox.

Chọn điểm I(1; 1) $\in$ d₂ và thay vào biểu thức y ta được 1 > 0.

Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d₂ chứa điểm I(1; 1).

• Vẽ đường thẳng d₃: 3x + y = 6 bằng cách vẽ đường thẳng đi qua hai điểm (2; 0) và (1; 3).

Chọn điểm I(1; 1) $\in$ d₃ và thay vào biểu thức 3x + y ta được 4 < 6.

Suy ra miền nghiệm của bất phương trình 3x + y ≤ 6 là nửa mặt phẳng bờ d₃ chứa điểm I(1; 1).

• Vẽ đường thẳng d₄: x + y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (4; 0) và (0; 4).

Chọn điểm I(1; 1) $\in$ d₄ và thay vào biểu thức x + y ta được 2 < 4.

Suy ra miền nghiệm của bất phương trình x + y ≤ 4 là nửa mặt phẳng bờ d₄ chứa điểm I(1; 1).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

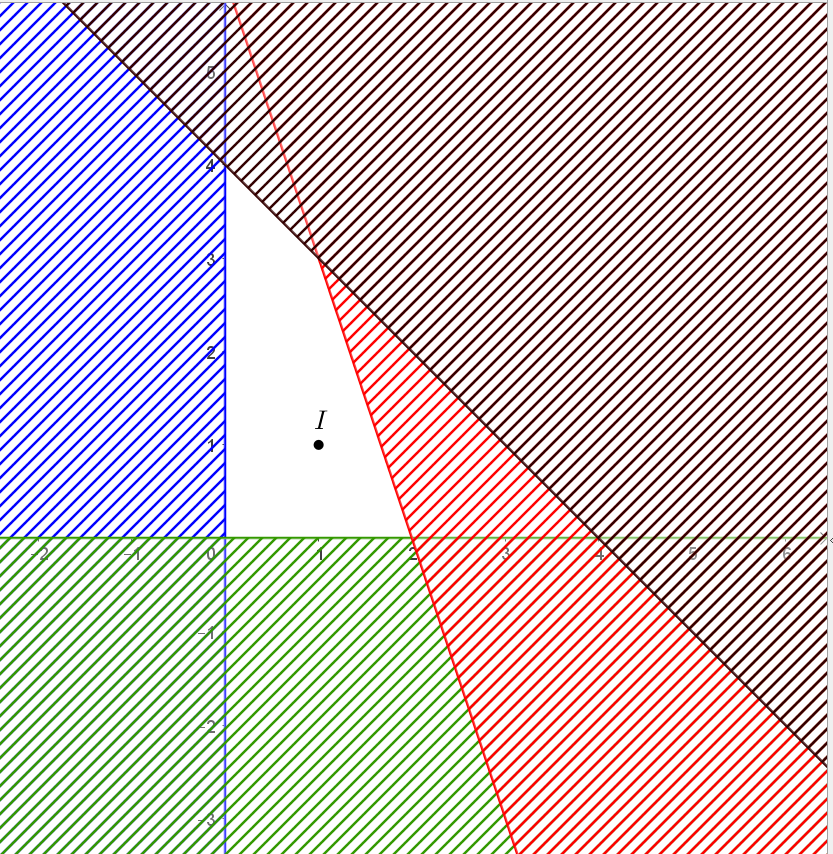
Ta thấy miền nghiệm của hệ bất phương trình trên là miền tứ giác với các đỉnh (0; 0), (0; 4), (1; 3), (2; 0).

Ta có:

F(0; 0) = 2 . 0 + 1,6 . 0 = 0;

F(0; 4) = 2 . 0 + 1,6 . 4 = 6,4;

F(1; 3) = 2 . 1 + 1,6 . 3 = 6,8;

F(2; 0) = 2 . 2 + 1,6 . 0 = 4.

Khi đó giá trị của F(x; y) lớn nhất bằng 6,8.

Vậy số tiền lãi lớn nhất một ngày mà phân xưởng có thể đạt được là 6,8 triệu đồng.

Bài 2.29 trang 28 SBT Toán 10 Tập 1:Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống I và II.

Mỗi cốc đồ uống I cung cấp 60 calo, 12 đơn vị vitamin A và 10 đơn vị vitamin C.Mỗi cốc đồ uống II cung cấp 60 calo, 6 đơn vị vitamin A và 30 đơn vị vitamin C. Biết rằng một cốc đồ uống I có giá 12 nghìn đồng và một cốc đồ uống II có giá 15 nghìn đồng.

a) Gọi x và y tương ứng là số cốc đồ uống I và II. Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình và xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x cốc đồ uống I và y cốc đồ uống II. Hãy biểu diễn F theo x và y.

c) Biết rằng F đạt giá trị nhỏ nhất trên miền nghiệm tìm được ở câu a tại một trong các đỉnh của miền nghiệm, tìm giá trị nhỏ nhất đó. Từ đó suy ra người đó cần uống bao nhiêu cốc loại I và loại II để chi phí là nhỏ nhất mà vẫn đáp ứng được yêu cầu hằng ngày.

Lời giải:

a) Do có x cốc đồ uống I và y cốc đồ uống II nên x ≥ 0; y ≥ 0.

x cốc đồ uống I cung cấp 60x calo, 12x đơn vị vitamin A và 10x đơn vị vitamin C.

y cốc đồ uống II cung cấp 60y calo, 6y đơn vị vitamin A và 30y đơn vị vitamin C.

Do người đó cần cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C nên 60x + 60y ≥ 300; 12x + 6y ≥ 36; 10x + 30y ≥ 90.

Khi đó ta có hệ bất phương trình sau: $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 60\text{x}+60y\ge 300\\ 12\text{x}+6y\ge 36\\ 10\text{x}+30y\ge 90\end{array}\right.\iff \left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\ge 5\\ 2\text{x}+y\ge 6\\ x+3y\ge 9\end{array}\right.$

Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:

• Đường thẳng d₁: x = 0 là đường thẳng trùng với trục Oy.

Chọn điểm I(3; 3) $\in$ d₁ và thay vào biểu thức x ta được 3 > 0.

Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d₁ chứa điểm I(3; 3).

• Đường thẳng d₂: y = 0 là đường thẳng trùng với trục Ox.

Chọn điểm I(3; 3) $\in$ d₂ và thay vào biểu thức y ta được 3 > 0.

Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d₂ chứa điểm I(3; 3).

• Vẽ đường thẳng d₃: x + y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; 5) và (5; 0).

Chọn điểm I(3; 3) $\in$ d₃ và thay vào biểu thức x + y ta được 6 > 5.

Suy ra miền nghiệm của bất phương trình x + y ≥ 5 là nửa mặt phẳng bờ d₃ chứa điểm I(3; 3).

• Vẽ đường thẳng d₄: 2x + y = 6 bằng cách vẽ đường thẳng đi qua hai điểm (0; 6) và (1; 4).

Chọn điểm I(3; 3) $\in$ d₄ và thay vào biểu thức x + y ta được 2 . 3 + 3 = 9 > 6.

Suy ra miền nghiệm của bất phương trình 2x + y ≥ 5 là nửa mặt phẳng bờ d₄ chứa điểm I(3; 3).

• Vẽ đường thẳng d₅: x + 3y = 9 bằng cách vẽ đường thẳng đi qua hai điểm (0; 3) và (3; 2).

Chọn điểm I(3; 3) $\in$ d₅ và thay vào biểu thức x + 3y ta được 2 + 3 . 3 = 11 > 5.

Suy ra miền nghiệm của bất phương trình x + 3y ≥ 9 là nửa mặt phẳng bờ d₅ chứa điểm I(3; 3).

Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:

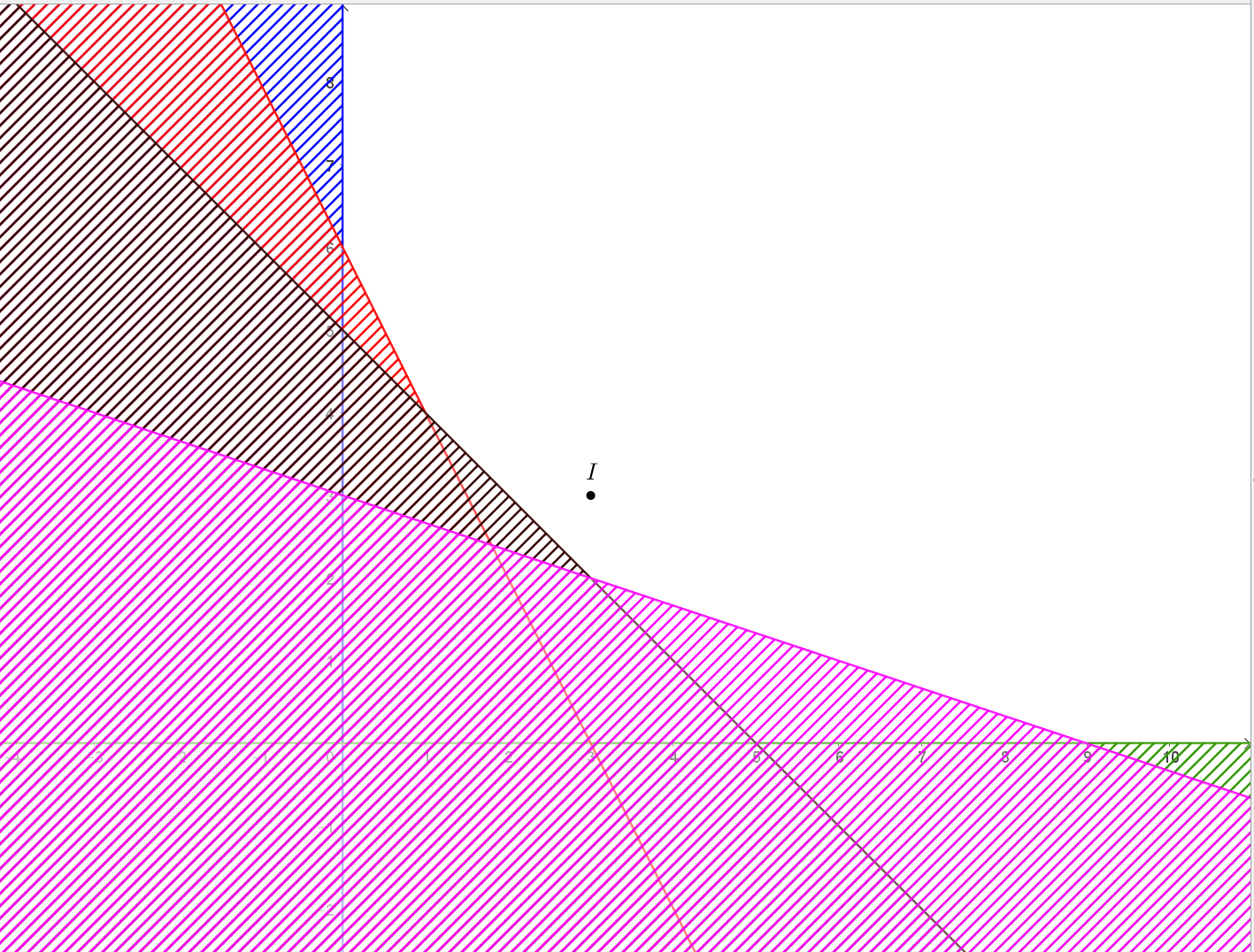
Ta thấy miền nghiệm của hệ bất phương trình trên là miền tứ giác với các đỉnh (0; 6), (1; 4), (3; 2), (9; 0).

b) Chi phí cho hai loại đồ uống là F(x; y) = 12x + 15y (nghìn đồng).

c) Ta có:

F(0; 6) = 12 . 0 + 15 . 6 = 90;

F(1; 4) = 12 . 1 + 15 . 4 = 72;

F(3; 2) = 12 . 3 + 15 . 2 = 66;

F(9; 0) = 12 . 9 + 15 . 0 = 108.

Giá trị nhỏ nhất của F(x; y) bằng 66 khi x = 3 và y = 2.

Vậy người đó cần uống 3 cốc đồ uống I và 2 cốc đồ uống II để đạt được các mục tiêu đã đề ra.

Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Bài 2: Tập hợp và các phép toán trên tập hợp

Bài tập cuối chương 1

Bài 3: Bất phương trình bậc nhất hai ẩn

Bài 4: Hệ bất phương trình bậc nhất hai ẩn

Bài 5: Giá trị lượng giác của một góc từ 0° đến 180°

Xem thêm tài liệu Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Lý thuyết Ôn tập chương 2