Nội dung bài viết

    Xem thêm

    Lý thuyết Dãy số – Toán 11 Cánh diều

    Với lý thuyết Toán lớp 11 Bài 1: Dãy số chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 11.

    1 1,946 15/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 11 Bài 1: Dãy số - Cánh diều

    A. Lý thuyết Dãy số

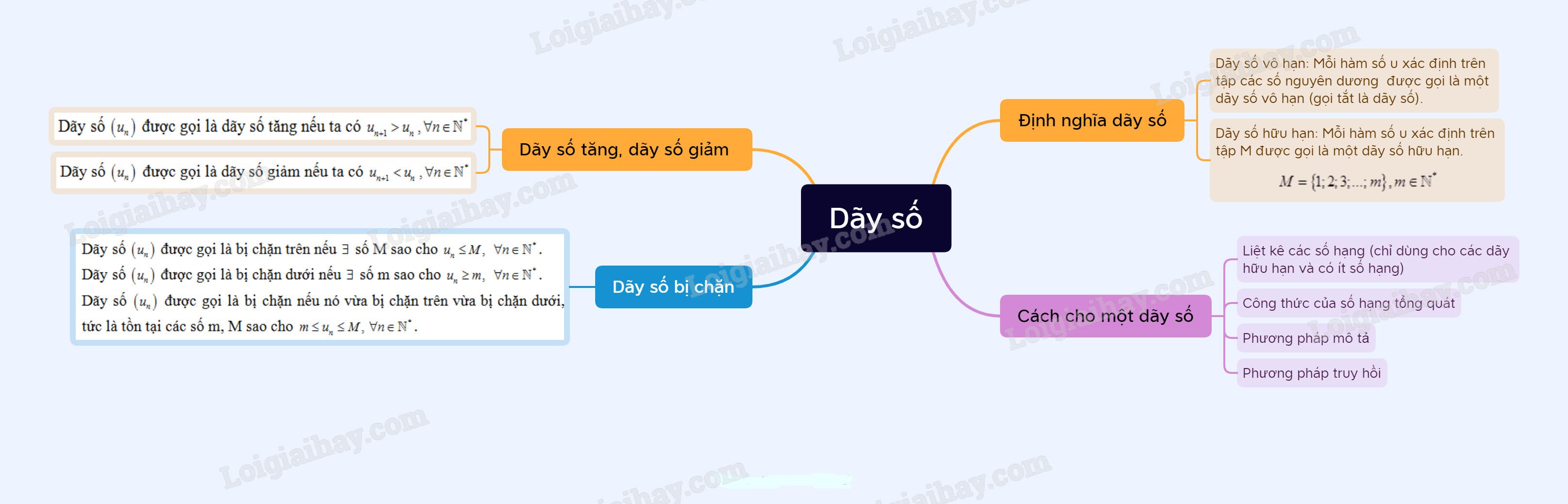
    I. Khái niệm

    • Dãy số hữu hạn

    Mỗi hàm số u: {1;2;3;...;m}→R(m∈N∗) được gọi là một dãy số hữu hạn.

    Do mỗi số nguyên dương k(1≤k≤m) tương ứng với đúng một số uk nên ta có thể viết dãy số đó dưới dạng khai triển: u1,u2,u3,...,um

    Số u1 là số hạng đầu; um là số hạng cuối cùng của dãy số đó.

    • Dãy số vô hạn

    Mỗi hàm số u: N∗→R được gọi là một dãy số vô hạn.

    Do mỗi số nguyên dương n tương ứng với đúng một số un nên ta có thể viết dãy số đó dưới dạng khai triển: u1,u2,u3,...,un,...

    Số u1 là số hạng đầu; un là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

    2. Cách cho một dãy số

    * Một dãy số có thể cho bằng:

    Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng).

    Công thức của số hạng tổng quát.

    Diễn đạt bằng lời cách xác định mỗi số hạn tổng quát của dãy số đó.

    Phương pháp truy hồi.

    3. Dãy số tăng, dãy số giảm

    Dãy số (un) được gọi là dãy số tăng nếu ta có un+1>un,∀n∈N∗.

    Dãy số (un) được gọi là dãy số giảm nếu ta có un+1<un,∀n∈N∗.

    4. Dãy số bị chặn

    Dãy số (un) được gọi là bị chặn trên nếu ∃ số M sao cho un≤M, ∀n∈N∗.

    Dãy số (un) được gọi là bị chặn dưới nếu ∃ số m sao cho un≥m, ∀n∈N∗.

    Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho m≤un≤M,∀n∈N∗.

    Lý thuyết Dãy số – Toán 11 Cánh diều (ảnh 1)

    B. Bài tập Dãy số

    Đang cập nhật ...

    Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 sách Cánh diều hay, chi tiết khác:

    Lý thuyết Bài 2: Cấp số cộng

    Lý thuyết Bài 3: Cấp số nhân

    Lý thuyết Bài 1: Giới hạn của dãy số

    Lý thuyết Bài 1: Giới hạn của hàm số

    Lý thuyết Bài 3: Hàm số liên tục

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,946 15/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: