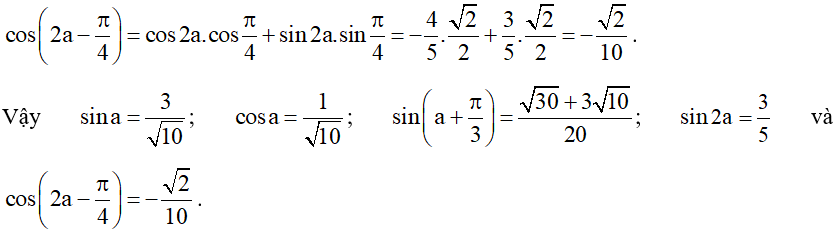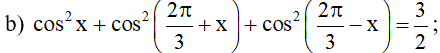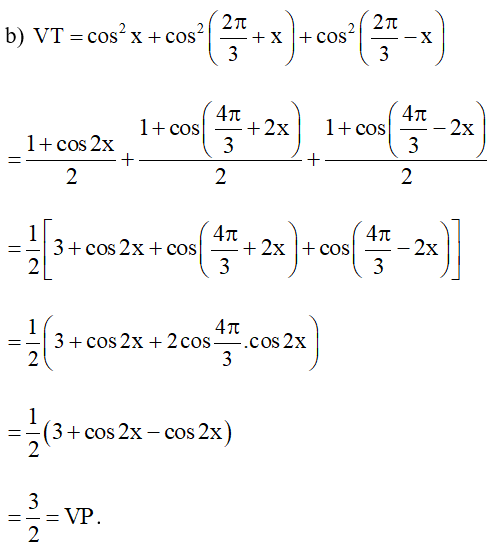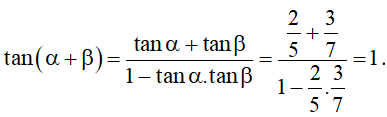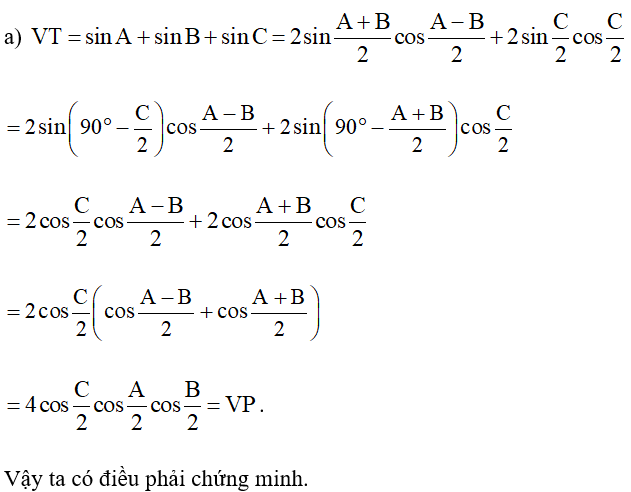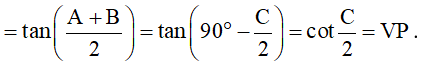Lý thuyết Các phép biến đổi lượng giác – Toán 11 Cánh diều
Với lý thuyết Toán lớp 11 Bài 2: Các phép biến đổi lượng giác chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 11.
Lý thuyết Toán 11 Bài 2: Các phép biến đổi lượng giác - Cánh diều
Bài giảng Toán 11 Bài 2: Các phép biến đổi lượng giác
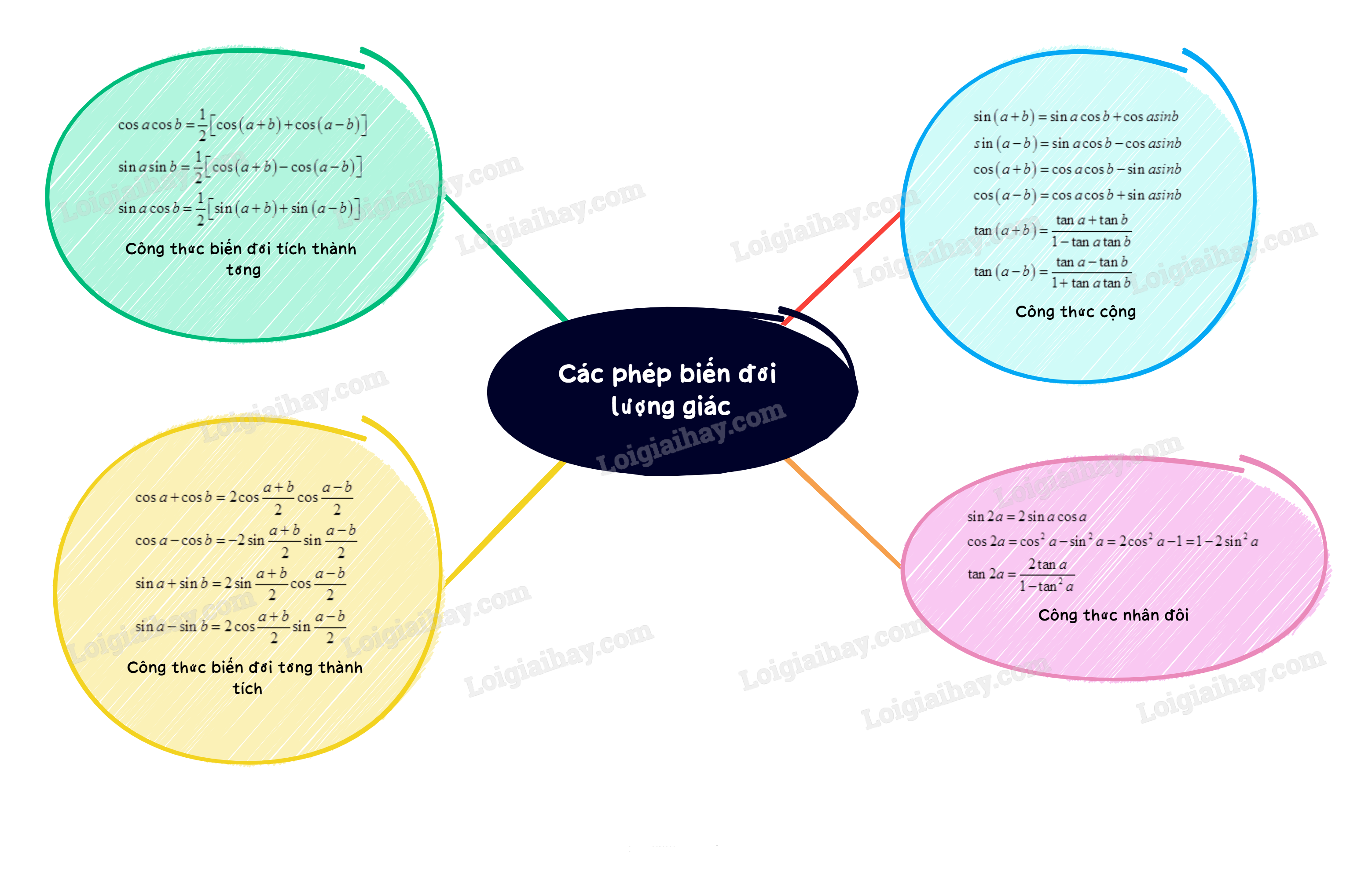
A. Lý thuyết Các phép biến đổi lượng giác
I. Công thức cộng
II. Công thức nhân đôi
Suy ra, công thức hạ bậc:
III. Công thức biến đổi tích thành tổng
IV. Công thức biến đổi tổng thành tích
B. Bài tập Các phép biến đổi lượng giác
Bài 1. Cho , với . Tính sina, cosa, 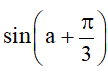
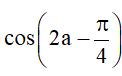
Hướng dẫn giải
Vì nên sina > 0, cosa > 0.
• Áp dụng công thức hạ bậc, ta được:
Suy ra (do sina > 0)
• Áp dụng công thức hạ bậc, ta được: .
Suy ra .
• Áp dụng công thức cộng đối với sin, ta được:
.
• Áp dụng công thức nhân đôi, ta được:
.
• Áp dụng công thức cộng đối với côsin, ta được:
Bài 2. Chứng minh rằng:
a) ;
Hướng dẫn giải
a) VT = cos3x.sinx – sin3x.cosx
= cosx.sinx.(cos2x – sin2x)
= VP.
Vậy ta có điều phải chứng minh.
Bài 3. Tính α + β biết .
Hướng dẫn giải
Áp dụng công thức cộng đối với tang, ta được:
Vậy .
Bài 4. Cho ∆ABC. Chứng minh rằng:
a) ;
b) ;
c) , với R là bán kính đường tròn ngoại tiếp ∆ABC và S là diện tích ∆ABC.
Hướng dẫn giải
∆ABC, có: , suy ra
Do đó .
b)
Vậy ta có điều phải chứng minh.
c) VT = sin2A + sin2B + sin2C
= 2sin(A + B).cos(A – B) + 2sinC.cosC
= 2sin(180° – C).cos(A – B) + 2sinC.cosC
= 2sinC.cos(A – B) + 2sinC.cosC
= 2sinC.[cos(A – B) + cosC]
= 2sinC.[cos(A – B) + cos(180° – A – B)]
= 2sinC.[cos(A – B) – cos(A + B)]
= –4sinC.sinA.sin(–B)
= 4sinA.sinB.sinC
.
Vậy ta có điều phải chứng minh.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 sách Cánh diều hay, chi tiết khác:
Lý thuyết Bài 3: Hàm số lượng giác và đồ thị
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều