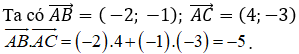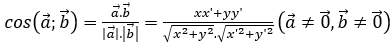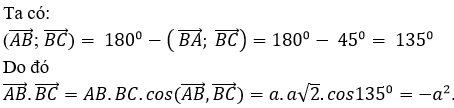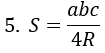100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản
100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P2)
-
1148 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
23/07/2024Trong mặt phẳng Oxy cho A(-1; 1) ; B(1; 3) và C(1; -1). Khẳng định nào sau đây đúng.
 Xem đáp án
Xem đáp án
Chọn C.

Câu 4:
23/07/2024Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn B.
Trong khoảng từ 900 đến 1800, khi giá trị của góc tăng thì:
- Giá trị sin tương ứng của góc đó giảm.
- Giá trị cos tương ứng của góc đó giảm.
Câu 5:
23/07/2024Cho tam giác ABC vuông tại A có góc B = 600, AB = a Tính
 Xem đáp án
Xem đáp án
Chọn B.
Ta có:
Do đó;
Câu 6:
17/07/2024Cho tam giác ABC có đường cao BH ( H ở trên cạnh AC).Câu nào sau đây đúng
 Xem đáp án
Xem đáp án
Chọn C.
Ta có BH và CA vuông góc với nhau nên và
Câu 7:
22/07/2024Cho tam giác ABC. Lấy điểm M trên BC sao cho .Câu nào sau đây đúng
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
nên AM ⊥ BC.
Câu 8:
18/07/2024Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a. Tính
 Xem đáp án
Xem đáp án
Chọn A.
Từ giả thiết ta suy ra:
Do đó
Câu 9:
17/07/2024Cho tam giác ABC vuông tại C có AC = 9; BC = 5. Tính
 Xem đáp án
Xem đáp án
Chọn B.
Do tam giác ABC vuông tại C nên
Ta có
Câu 10:
12/07/2024Giá trị của tan 450 + cot1350+ sin900 bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn B.
Dùng bảng giá trị lượng giác các góc đặc biệt ta có:
tan 450 + cot1350 + sin900 = 1 - 1 + 1 = 1.
Câu 11:
14/07/2024Giá trị của cos300 + sin600 bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn C.
Dùng bảng giá trị lượng giác các góc đặc biệt ta có
Câu 12:
14/07/2024Cho biết sin+cos = a. Giá trị của sin.cos bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn D.
Ta có:
Câu 13:
21/07/2024Cho tam giác đều ABC có đường cao AH. Tính
 Xem đáp án
Xem đáp án
Chọn D.
Ta có:
(tam giác ABC là tam giác đều; AH là đường cao nên góc HAB = 300
Câu 15:
09/10/2024Cho biết cosα = -2/3. Tính tanα biết tanα > 0.
 Xem đáp án
Xem đáp án
Đáp án đúng: C
*Phương pháp giải:
- Áp dụng tính chất của giá trị lượng giác đặc biệt, quy tắc nhân lượng giác, hằng đẳng thức để thực hiên phép tính
*Lời giải:
Ta có:
(vì tanα > 0).
*Các lý thuyết cần nằm về lượng giác
a. Công thức cộng:
b. Công thức nhân đôi, hạ bậc:
* Công thức nhân đôi:
* Công thức hạ bậc:
* Công thức nhân ba:
c. Công thức biến đổi tích thành tổng:
d. Công thức biển đổi tổng thành tích:
|
|
|
*Các dạng bài lượng giác của một góc bất kì từ 0-180a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).Xem thêm các bài viết liên quan hay, chi tiết:
TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản
Câu 18:
12/07/2024Cho hai vectơ thỏa mãn và . Xác định góc giữa hai vectơ đó
 Xem đáp án
Xem đáp án
Chọn D.
Ta có nên
Câu 19:
17/07/2024Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng
 Xem đáp án
Xem đáp án
Chọn D.
Ta có góc là góc BAC nên
Do đó
Câu 20:
12/10/2024Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng
 Xem đáp án
Xem đáp án
Đáp án đúng: A.
*Phương pháp giải:
- Xem lại định nghĩa góc xen giữa 2 vecto: ở đây góc xen giữa 2 vectơ AB và BC là góc ABC và số đo = 180 - số đo góc ACB. từ đó tìm ra kết quả bằng công thức tích vô hướng 2 vectơ
*Lời giải:

*Lý thuyết về tích vô hướng và có hướng của 2 vectơ:
Phương pháp 1: Sử dụng định nghĩa góc giữa hai vectơ
Định nghĩa góc giữa hai vectơ: Cho hai vectơ 
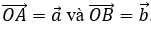


Phương pháp 2: (Áp dụng trong hệ tọa độ) Tính cos góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ. Sử dụng công thức sau: Cho hai vectơ 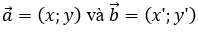
Chú ý: Góc giữa hai vectơ thuộc [0°;180°]
Cách tính tích vô hướng của 2 vectơ:
Trong không gian, cho hai vectơ u→ và v→ đều khác 0→ . Tích vô hướng của hai vectơ u→ và v→ là một số, kí hiệu là u→. v→, được xác định bởi công thức:
Trong trường hợp u→ = 0→ hoặc v→ = 0→, ta quy ước u→. v→ = 0
Xem thêm các bài viết liên quan hay, chi tiết
Tích vô hướng của hai vectơ và cách giải bài tập
Câu 22:
18/07/2024Cho ba điểm A; B; C thỏa mãn có AB = 2 cm; BC = 3cm; CA = 5cm. Tính
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: AB + BC = AC nên ba điểm A; B; C thẳng hàng và B nằm giữa A; C
Khi đó
Câu 23:
19/07/2024Trong mặt phẳng tọa độ Oxy cho ba điểm A( 2; -1) ; B( 2; 10) và C(-4; 2). Tính tích vô hướng
 Xem đáp án
Xem đáp án
Chọn A.
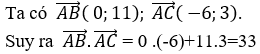
Câu 24:
19/07/2024Cho tam giác ABC có b = 6 và c = 8; góc A bằng 60 độ. Độ dài cạnh a là:
 Xem đáp án
Xem đáp án
Chọn B.
Áp dụng định lí cosin cho tam giác ta có:
a2 = b2 + c2 - 2bc.cosA = 36 + 64 - 2.6.8.cos600 = 52
do đó .
Câu 25:
10/11/2024Cho tam giác MNP có S = 84; a =13; b = 14; c = 15. Độ dài bán kính đường tròn ngoại tiếp của tam giác trên gần với số nào nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là C.
Lời giải:
Ta có:
*Phương pháp giải
Sử dụng công thức diện tích từ đó suy ra R
*Lý thuyết
Với S diện tích, h chiều cao, p=(a+b+c)/2 nửa chu vi, r bán kính nội tiếp, R bán kính ngoại tiếp, trung tuyến AM, phân giác AD.
Xem thêm
Các công thức tính diện tích tam giác (2024) đầy đủ, chi tiết nhất
TOP 40 câu Trắc nghiệm Diện tích tam giác (có đáp án ) - Toán 8
Bài thi liên quan
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P1)
-
25 câu hỏi
-
30 phút
-
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P3)
-
25 câu hỏi
-
30 phút
-
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P4)
-
25 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Hình học Ôn tập chương 2 (có đáp án) (835 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (1147 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (1192 lượt thi)
- Trắc nghiệm ôn tập chương 2 Tích vô hướng của hai vectơ và ứng dụng có đáp án (262 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Nhận biết) (263 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Thông hiểu) (254 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Vận dụng) (257 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (280 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án) (2926 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ (có đáp án) (2544 lượt thi)
- Trắc nghiệm: Giá trị lượng giác của một góc bất kì 0° đến 180° (535 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Nhận biết) (535 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Vận dụng) (507 lượt thi)
- Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án (480 lượt thi)
- Trắc nghiệm: Hệ thức lượng trong tam giác có đáp án (459 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Nhận biết) (416 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Vận dụng) (400 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Thông hiểu) (381 lượt thi)