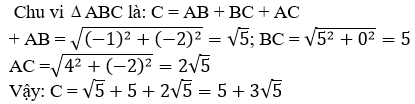100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P3)
-
1043 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
13/07/2024Cho tam giác ABC có a = 3; b = 4 và c = 5. Diện tích S của tam giác trên là:
Xem đáp án
Chọn B.
Ta có: Nửa chu vi tam giác là: (3 + 4 + 5) : 2 = 6.
Áp dụng công thức Hê rông:
Câu 2:
21/07/2024Trong mặt phẳng tọa độ; cho 2 điểm A(1; 2) và B(4; 6). Tính khoảng cách giữa hai điểm đó.
Xem đáp án
Chọn D.
Câu 3:
20/07/2024Cho tam giác ABC có , nửa chu vi p = 10. Độ dài bán kính đường tròn nội tiếp của tam giác trên là:
Xem đáp án
Chọn C.
Ta có: 
Câu 4:
21/07/2024Cho tam giác ABC có a = 4; c = 5; B = 1500. Diện tích của tam giác là:
Xem đáp án
Chọn B.
Ta có: 
Câu 5:
18/07/2024Tam giác ABC có AB = 6 ; AC = 8 và BC = 10. Độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác bằng:
Xem đáp án
Chọn D.
Cách 1: Áp dụng công thức đường trung tuyến 
ta được:
Suy ra ma = 5
Cách 2: nhận xét đây là tam giác vuông tại A nên ma = 1/2. BC = 5.
Câu 6:
17/07/2024Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho.
Xem đáp án
Chọn D.
Gọi M là trung điểm của AC suy ra
.
Do tam giác BAM vuông tại A
Câu 7:
18/07/2024Tam giác ABC có AB = 9; AC = 12 và BC = 15cm. Tính độ dài đường trung tuyến AM của tam giác đã cho.
Xem đáp án
Chọn A.
Áp dụng hệ thức đường trung tuyến 
ta được:
Suy ra : ma= 7,5.
Câu 8:
13/07/2024Tam giác ABC có AB = 5; BC = 7 và CA = 8. Số đo góc A bằng:
Xem đáp án
Chọn B.
Theo định lí hàm cosin, ta có
Do đó 
Câu 9:
13/07/2024Trong mặt phẳng tọa độ Oxy cho hai vectơ . Khẳng định nào sau đây đúng?
Xem đáp án
Chọn C.
Ta có 
suy ra hai vecto vuông góc với nhau.
Câu 10:
06/10/2024Rút gọn biểu thức sau A = (tanx + cotx)2 - ( tanx - cotx)2
Xem đáp án
Đáp án đúng: B.
*Phương pháp giải:
- Áp dụng tính chất của giá trị lượng giác đặc biệt, quy tắc nhân lượng giác, hằng đẳng thức để thực hiên phép tính
*Lời giải:
Ta có: tanx.cotx = 1
Khi đó: A = (tanx + cotx)2 - ( tanx - cotx)2
= tan2x + 2tanx.cot x + cot2x - ( tan2x - 2tanx.cotx + cot2x)
= tan2x + 2tanx.cot x + cot2x - tan2x + 2tanx.cotx - cot2x
= 4tanx.cotx = 4.*Các dạng bài lượng giác của một góc bất kì từ 0-180a) Dạng 1: Góc và dấu của các giá trị lượng giác *Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.b) Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.c) Dạng 3: Chứng minh, rút gọn biểu thức lượng giác*Phương pháp: Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).Xem thêm các bài viết liên quan hay, chi tiết:
TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản
50 Bài tập Hàm số lượng giác mới nhất
Câu 11:
18/09/2024Đơn giản biểu thức C = (1- sin2x) cot2x + 1 - cot2x.
Xem đáp án
Chọn A.
Ta có C = (1-sin2x) cot2x + 1 - cot2x.
= (1 - sin2x - 1) cot2x + 1
= -sin2x.cot2x + 1 = -cos2x + 1 = sin2x.
* Một số công thức cần nhớ để áp dụng
1. Công thức cộng
2. Công thức nhân đôi
Suy ra, công thức hạ bậc:
3. Công thức biến đổi tích thành tổng
4. Công thức biến đổi tổng thành tích
Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:
Câu 12:
21/07/2024Câu nào sau đây là phương tích của điểm M(1;2) đối với đường tròn (C) có tâm I(-2;1), bán kính R = 2:
Xem đáp án
Chọn B.
Ta có: 
Phương tích của điểm M đối với đường tròn (C) tâm I là:
MI2 - R2 = 10 – 4 = 6
Câu 13:
13/07/2024Một tam giác có ba cạnh là 30; 26; 28. Bán kính đường tròn nội tiếp là:
Xem đáp án
Chọn B.
Ta có nửa chu vi của tam giác đã cho là:
P = (30 + 26 +28) : 2 = 42
Câu 14:
23/07/2024Cho tam giác ABC có a = 4; b = 6; c = 8. Khi đó diện tích của tam giác là:
Xem đáp án
Chọn B.
Nửa chu vi của tam giác là p = (4 + 6 + 8) : 2 = 9
Áp dụng công thức Hê-rông
Suy ra: 
Câu 15:
15/07/2024Tam giác với ba cạnh là 5; 12; 13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu ?
Xem đáp án
Chọn A.
Ta có nửa chu vi của tam giác đã cho là:
(5 + 12 + 13) : 2 = 15
Mà 52 + 122 = 132 nên tam giác đã cho là tam giác vuông có diện tích là:
S = 1/2 .5.12 = 30
Mặt khác S = pr nên 
Câu 16:
17/07/2024Cho tam giác ABC, biết a = 24; b = 13 và c = 15. Tính góc A?
Xem đáp án
Chọn D.
Áp dụng định lí cosin trong tam giác ta có:
Suy ra: A = 1170 49’
Câu 17:
20/07/2024Tam giác ABC có A = 68012’; B = 34044’, AB =117. Hỏi AC gần với giá trị nào nhất.
Xem đáp án
Chọn A
Trong tam giác ABC:
Theo định lí sin trong tam giác ta có:
Câu 18:
21/07/2024Cho tam giác ABC có AB = 10; AC = 4 và góc A bằng 600. Tính chu vi của tam giác.
Xem đáp án
Chọn B.
Theo định lí côsin ta có
BC2 = AB2 + AC2 - 2.AB.AC.cos A = 102 + 42 - 2.10.4.cos 60 = 76
Suy ra BC ≈ 8,72
Suy ra chu vi tam giác là 10 + 4 + 8,72 = 22,72
Câu 19:
22/07/2024Cho tam giác ABC, Tìm mệnh đề đúng.
Xem đáp án
Chọn D.
Ta có: A + B + C = 1800 ⇒ A = 1800 – (B + C)
Khi đó: sinA = sin(1800 – (B + C)) = sin(B + C)
Câu 20:
13/07/2024Cho góc x, với cosx = 2/3. Tính giá trị của biểu thức: P = 5sin2x + 2cos2x.
Xem đáp án
Chọn C.
Ta có: sin2x + cos2x = 1 ⇒ sin2x = 1 – cos2x = 1 – 4/9 = 5/9
Vậy: 
Câu 23:
13/07/2024Tìm m để góc giữa 2 vecto và bằng 1800
Xem đáp án
Chọn A.
Để góc giữa 2 vecto 
bằng 1800 thì 2 vecto ban đầu là ngược hướng
Do đó; m = -4.
Câu 24:
13/07/2024Cho tam giác ABC với A(2; 4), B(1; 2), C(6; 2). Hỏi tam giác ABC là tam giác gì?
Xem đáp án
Chọn D.
Ta có: 
suy ra 
do đó; 2 vecto AB và AC vuông góc với nhau
suy ra tam giác ABC vuông tại A.
