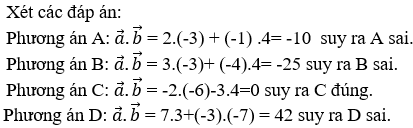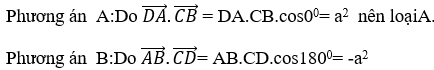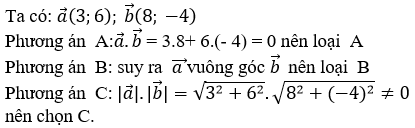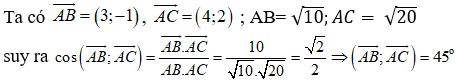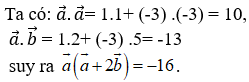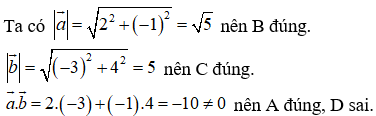100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản
100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P1)
-
1296 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
13/07/2024Giá trị biểu thức A = cos 450 + 3.sin 450 bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn B.
Ta có:
Nên A = cos 450 + 3.sin 450 = .
Câu 2:
13/11/2024Giá trị của tan 300+ cot 300 bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là A.
Lời giải
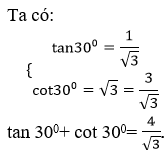
* Phương pháp giải
- Sử dụng bảng giá trị lượng giác của các góc đặc biệt để tìm ra giá trị của tan30 và cot30 rồi cộng chúng lại với nhau
* Lý thuyết
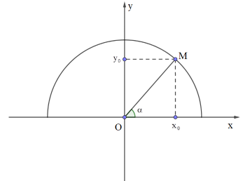
- Định nghĩa: Cho góc α (0o≤α≤180o) bất kì, xác định một điểm M(x0;y0) trên nửa đường tròn đơn vị sao cho ^xOM=α. Khi đó ta có: sinα=y0; cosα=x0; tanα=y0x0(x0≠0); cotα=x0y0(y0≠0). ( sin, cos, tan, cot là các giá trị lượng giác của góc α)
Bảng giá trị lượng giác của các góc đặc biệt:
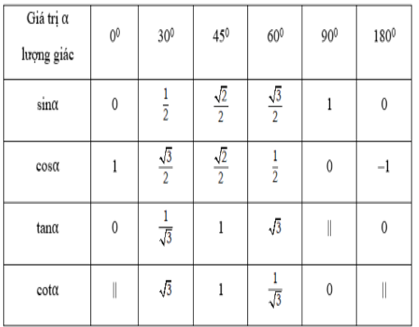
CẤC DẠNG BÀI:
Dạng 1: Góc và dấu của các giá trị lượng giác.
Phương pháp giải:
Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.
Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại.
Phương pháp giải:
Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.
Dạng 3: Chứng minh, rút gọn một biểu thức lượng giác.
Phương pháp giải:
Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).
Xem thêm
Câu 3:
23/07/2024Cho →a và →b là hai vectơ cùng hướng và đều khác vectơ →0. Trong các kết quả sau đây, hãy chọn kết quả đúng:
 Xem đáp án
Xem đáp án
Chọn A.
Do và
là hai vectơ cùng hướng và đều khác vectơ
suy ra
Do đó
Câu 4:
12/07/2024Cho các vectơ →a(1;-2);→b(-2;-6). Khi đó góc giữa chúng là
 Xem đáp án
Xem đáp án
Chọn A.
Ta có: nên
suy ra
Câu 6:
21/07/2024Trong mặt phẳng Oxy cho →a(1;3) và →b(-2;1). Tích vô hướng →a.→blà:
 Xem đáp án
Xem đáp án
Chọn C.
![]()
Câu 8:
15/07/2024Cho tam giác ABC cân tại A; góc A = 1200 và AB = a. Tính →BA.→CA
 Xem đáp án
Xem đáp án
Chọn B.

Câu 9:
12/07/2024Trong mặt phẳng Oxy cho A(-1; -1) ; B(3; 1) và C(6; 0). Khẳng định nào sau đây đúng.
 Xem đáp án
Xem đáp án
Chọn B.
Xét các phương án:
Phương án A: do nên loại A
Phương án B:
Ta có suy ra
Câu 11:
17/07/2024Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD . Khi đó bằng :
 Xem đáp án
Xem đáp án
Chọn B.
Do I là trung điểm AD nên IA = ID = 3a/2
Ta có
Câu 13:
12/07/2024Tam giác ABC vuông ở A và có góc . Hệ thức nào sau đây là sai?
 Xem đáp án
Xem đáp án
Chọn D.

Câu 14:
21/07/2024Trong mp Oxy cho A( 4; 6); B(1;4); C(7; 3/2). Khẳng định nào sau đây sai
 Xem đáp án
Xem đáp án
Chọn D.
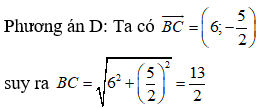
Câu 18:
20/07/2024Cho hình vuông ABCD, tính
 Xem đáp án
Xem đáp án
Chọn D.
Đầu tiên ta đi tìm số đo của góc sau đó mới tính
Vì
Câu 19:
12/07/2024Cho tam giác ABC vuông cân tại A có AB = a. Tính
 Xem đáp án
Xem đáp án
Chọn A.
Do tam giác vuông cân tại A nên AB = AC = a và và góc C = 450
Ta có
Câu 22:
12/07/2024Trong các khẳng định sau đây, khẳng định nào sai?
 Xem đáp án
Xem đáp án
Chọn D.
Dựa vào bảng giá trị lượng giác của các góc đặc biệt ta được
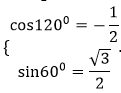
Câu 23:
12/07/2024Tam giác ABC vuông ở A có góc B = 300 . Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Chọn A.
Từ giả thiết suy ra góc C = 600
Dùng bảng giá trị lượng giác các góc đặc biệt ta có:
; sin C = 0,5 ; sinB = 0,5.
Câu 24:
12/07/2024Cho hai vecto đều khác vecto-không và . Câu nào sau đây đúng
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
Nên hai vecto đã cho là ngược hướng.
Bài thi liên quan
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P2)
-
25 câu hỏi
-
30 phút
-
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P3)
-
25 câu hỏi
-
30 phút
-
-
100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (P4)
-
25 câu hỏi
-
30 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Hình học Ôn tập chương 2 (có đáp án) (890 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (1295 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (1356 lượt thi)
- Trắc nghiệm ôn tập chương 2 Tích vô hướng của hai vectơ và ứng dụng có đáp án (313 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Nhận biết) (305 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Thông hiểu) (302 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (Vận dụng) (309 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 2 Hình học có đáp án (318 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án) (3079 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ (có đáp án) (2646 lượt thi)
- Trắc nghiệm: Giá trị lượng giác của một góc bất kì 0° đến 180° (585 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Nhận biết) (574 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Vận dụng) (547 lượt thi)
- Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án (541 lượt thi)
- Trắc nghiệm: Hệ thức lượng trong tam giác có đáp án (516 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Nhận biết) (464 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Vận dụng) (440 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Thông hiểu) (413 lượt thi)