Nội dung bài viết

    Xem thêm

    Giải Toán 8 trang 72 Chân trời sáng tạo

    Với giải bài tập Toán 8 trang 72 trong Bài 3: Hình thang – Hình thang cân sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 trang 72.

    1 641 23/04/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 trang 72

    Bài 3 trang 72 Toán 8 Tập 1: Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH và cắt AB tại N. Chứng minh rằng:

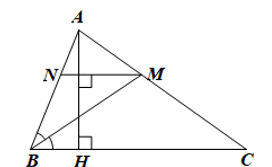
    a) Tứ giác BCMN là hình thang;

    b) BN = MN.

    Lời giải:

    Bài 3 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    a) Ta có AH ⊥ BC, AH ⊥ NM nên BC // NM

    Tứ giác BCMN có BC // NM nên là hình thang.

    b) Do BC // NM nên BMN^=MBC^ (so le trong).

    Mà NBM^=MBC^ (do BM là tia phân giác của ABC^)

    Suy ra NBM^=BMN^=MBC^

    Tam giác BMN có NBM^=BMN^ nên là tam giác cân tại N

    Suy ra BN = MN.

    Bài 4 trang 72 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA.

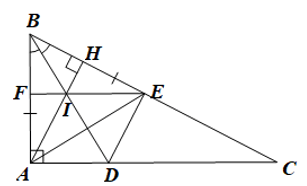
    a) Chứng minh rằng DABD = DEBD.

    b) Kẻ đường cao AH của tam giác ABC. Chứng minh rằng tứ giác ADEH là hình thang vuông.

    c) Gọi I là giao điểm của AH với BD, đường thẳng EI cắt AB tại F. Chứng minh rằng tứ giác ACEF là hình thang vuông.

    Lời giải:

    Bài 4 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    a) Xét DABD và DEBD có:

    BA = BE (giả thiết);

    ABD^=EBD^ (do BD là tia phân giác của ABE^);

    BD là cạnh chung,

    Do đó DABD = DEBD (c.g.c).

    b) Do DABD = DEBD (câu a) nên BAD^=BED^=90° (hai góc tương ứng).

    Do đó DE ⊥ BC

    Mà AH ⊥ BC (giả thiết) nên DE // AH.

    Tứ giác ADEH có DE // AH nên là hình thang

    Lại có AHE^=90° nên ADEH là hình thang vuông.

    c) Do DABD = DEBD (câu a) nên AD = ED (hai cạnh tương ứng)

    Do đó D nằm trên đường trung trực của AE.

    Lại có BA = BE (giả thiết) nên B nằm trên đường trung trực của AE.

    Suy ra BD là đường trung trực của đoạn thẳng AE nên BD ⊥ AE, hay BI ⊥ AE.

    Xét DABE có AI ⊥ BE, BI ⊥ AE nên I là trực tâm của tam giác

    Do đó EI ⊥ AB hay EF ⊥ AB.

    Mà CA ⊥ AB (do DABC vuông tại A)

    Suy ra EF // CA.

    Tứ giác ACEFF có EF // CA nên là hình thang.

    Lại có FAC^=90° nên ACEFF là hình thang vuông.

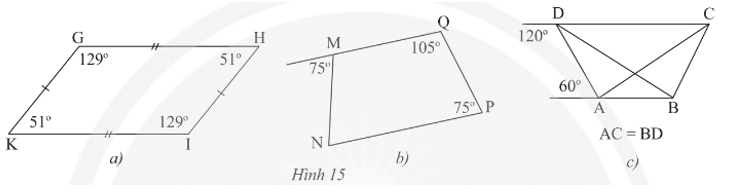
    Bài 5 trang 72 Toán 8 Tập 1: Tứ giác nào trong Hình 15 là hình thang cân?

    Bài 5 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Lời giải:

    • Hình 15a):

    Ta thấy hai góc kề một đáy của tứ giác GHIK có số đo là 51° và 129° không bằng nhau.

    Do đó tứ giác GHIK không phải là hình thang cân.

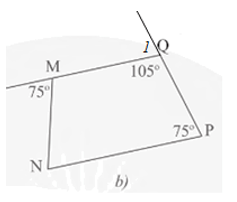
    • Hình 15b):

    Bài 5 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Ta có Q^1+MQP^=180° (hai góc kề bù) nên

    Q^1=180°−MQP^=180°−105°=75°.

    Do đó Q^1=P^=75°

    Mà hai góc này ở vị trí đồng vị nên MQ // NP.

    Tứ giác MNPQ có MQ // NP nên là hình thang.

    Do MQ // NP nên N^=75° (góc N so le trong với góc ngoài tại đỉnh M của hình thang)

    Do đó N^=P^=75°.

    Hình thang MNPQ có hai góc kề một đáy bằng nhau N^=P^ nên là hình thang cân.

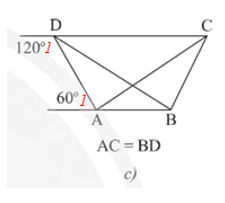
    • Hình 15c):

    Bài 5 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Ta có ADC^+D^1=180° (hai góc kề bù)

    Suy ra ADC^=180°−D^1=180°−120°=60°

    Do đó ADC^=A^1=60°, mà hai góc này ở vị trí so le trong nên DC // AB.

    Tứ giác ABCD có DC // AB và AC = BD nên là hình thang cân.

    Bài 6 trang 72 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB và cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác của góc CEB.

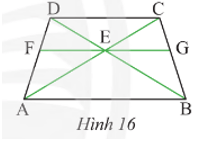
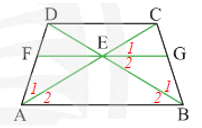
    Bài 6 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Lời giải:

    Bài 6 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Do ABCD là hình thang cân nên AB // DC và AD = BC; AC = BD; DAB^=CBA^ (tính chất hình thang cân).

    Xét DACD và DBDC có:

    CD là cạnh chung;

    AD = BC (chứng minh trên);

    AC = BD (chứng minh trên).

    Do đó DACD = DBDC (c.c.c)

    Suy ra A^1=B^1 (hai góc tương ứng)

    Lại có DAB^=CBA^ (chứng minh trên)

    Nên DAB^−A^1=CBA^−B^1 hay A^2=B^2.

    Mặt khác EG // AB nên E^1=A^2 (đồng vị) và E^2=B^2 (so le trong).

    Suy ra E^1=E^2, do đó EG là tia phân giác của góc CEB.

    Bài 7 trang 72 Toán 8 Tập 1: Mặt bên của một chiếc va li (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là 60 cm, cạnh bên là 61 cm và đáy lớn là 92 cm. Tính độ dài đáy nhỏ.

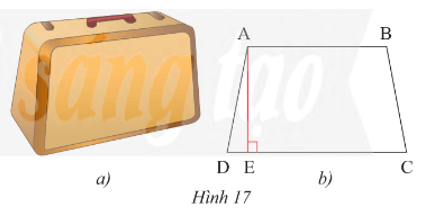
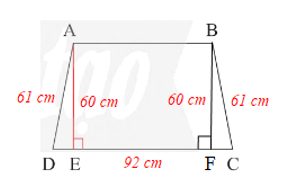
    Bài 7 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Lời giải:

    Bài 7 trang 72 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Áp dụng định lí Pythagore vào DADE vuông tại E, ta có:

    AD2 = AE2 + DE2

    Suy ra DE2 = AD2 – AE2 = 612 – 602 = 3 721 – 3 600 = 121 = 112

    Do đó DE = 11 cm.

    Kẻ BF ⊥ CD, khi đó BF là đường cao của hình thang cân ABCD nên BF = 60 cm.

    Xét DADE và DBCF có:

    AED^=BFC^=90°;

    AD = BC (do ABCD là hình thang cân);

    ADE^=BCF^ (do ABCD là hình thang cân).

    Do đó DADE = DBCF (cạnh huyền – góc nhọn)

    Suy ra DE = CF = 11 cm (hai cạnh tương ứng).

    Mà DE + EF + CF = DC

    Nên EF = DC – DE – CF = 92 – 11 – 11 = 70 cm.

    Tương tự Vận dụng 4, trang 71, Sách giáo khoa Toán 8, tập một, ta dễ dàng chứng minh được AB = EF = 70 cm.

    Vậy độ dài đáy nhỏ của hình thang cân là 70 cm.

    Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác: 

    Giải Toán 8 trang 68

    Giải Toán 8 trang 69

    Giải Toán 8 trang 70

    Giải Toán 8 trang 71

    Giải Toán 8 trang 72

    Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác: 

    Khởi động trang 68 Toán 8 Tập 1: Mái ngói của trụ sở Ủy ban nhân dân Thành phố Hồ Chí Minh có hình dạng một tứ giác ABCD...

    Khám phá 1 trang 68 Toán 8 Tập 1: Tứ giác ABCD (Hình 1b) là hình vẽ minh hoạ một phần của chiếc thang ở Hình la. Nêu nhận xét của em về hai cạnh AB và CD của tứ giác này...

    Thực hành 1 trang 69 Toán 8 Tập 1: Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em...

    Vận dụng 1 trang 69 Toán 8 Tập 1: Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân ABCD (Hình 4). Cho biết D^=C^=75°...

    Vận dụng 2 trang 69 Toán 8 Tập 1: Tứ giác EFGH có các góc cho như trong Hình 5.

    a) Chứng minh rằng EFGH là hình thang...

    Khám phá 2 trang 69 Toán 8 Tập 1: a) Cho hình thang cân ABCD có hai đáy là AB và CD (AB > CD). Qua C vẽ đường thẳng song song với AD và cắt AB tại E (Hình 6a)...

    Thực hành 2 trang 70 Toán 8 Tập 1: Tìm các đoạn thẳng bằng nhau trong hình thang cân MNPQ có hai đáy là MN và PQ...

    Vận dụng 3 trang 70 Toán 8 Tập 1: Một khung cửa sổ hình thang cân có chiều cao 3 m, hai đáy là 3 m và 1 m (Hình 9)...

    Khám phá 3 trang 70 Toán 8 Tập 1: Cho hình thang ABCD có hai đáy là AB, CD và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua C, song song với BD và cắt AB tại E...

    Thực hành 3 trang 71 Toán 8 Tập 1: Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12...

    Vận dụng 4 trang 71 Toán 8 Tập 1: Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm...

    Bài 1 trang 71 Toán 8 Tập 1: Tìm x và y ở các hình sau...

    Bài 2 trang 71 Toán 8 Tập 1: Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang...

    Bài 3 trang 72 Toán 8 Tập 1: Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH và cắt AB tại N...

    Bài 4 trang 72 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA...

    Bài 5 trang 72 Toán 8 Tập 1: Tứ giác nào trong Hình 15 là hình thang cân...

    Bài 6 trang 72 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB và cắt AD, BC lần lượt tại F và G (Hình 16)...

    Bài 7 trang 72 Toán 8 Tập 1: Mặt bên của một chiếc va li (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b...

    Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 2: Tứ giác

    Bài 3: Hình thang – Hình thang cân

    Bài 4: Hình bình hành – Hình thoi

    Bài 5: Hình chữ nhật – Hình vuông

    Bài tập cuối chương 3

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 641 23/04/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: