Nội dung bài viết

    Xem thêm

    Vận dụng 3 trang 70 Toán 8 Tập 1 | Chân trời sáng tạo Giải Toán 8

    Lời giải Vận dụng 3 trang 70 Toán 8 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 Tập 1.

    1 686 23/04/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Bài 3: Hình thang – Hình thang cân   

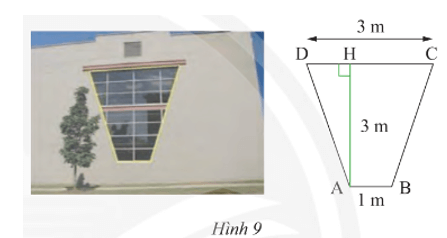
    Vận dụng 3 trang 70 Toán 8 Tập 1: Một khung cửa sổ hình thang cân có chiều cao 3 m, hai đáy là 3 m và 1 m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.

    Vận dụng 3 trang 70 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Lời giải:

    Vận dụng 3 trang 70 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

    Xét hình thang cân ABCD (AB // DC) có D^=C^; AD = BC và AC = BD (tính chất hình thang cân).

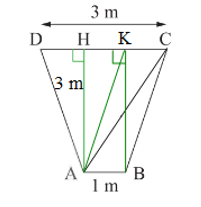
    Kẻ BK ⊥ DC.

    Ta có AB // DC và BK ⊥ DC

    Suy ra BK ⊥ AB nên ABK^=90°.

    Xét DAHK và DABK có:

    KHA^=ABK^=90°;

    AK là cạnh chung;

    AKH^=KAB^ (hai góc so le trong của DC // AB).

    Do đó DAHK = DABK (cạnh huyền – góc nhọn)

    Suy ra HK = BK = 1 cm (hai cạnh tương ứng).

    Xét DAHD và DBKC có:

    AHD^=BKC^=90°;

    AD = BC (chứng minh trên);

    D^=C^ (chứng minh trên).

    Do đó DAHD = DBKC (cạnh huyền – góc nhọn).

    Suy ra DH = CK (hai cạnh tương ứng).

    Mà DH + HK + CK = DC

    Hay 2DH = DC – HK

    Khi đó DH=CK=DC−HK2=3−12=1 (cm) và HC = 2 cm.

    Áp dụng định lí Pythagore cho DAHD vuông tại H, ta có:

    AD2 = AH2 + DH2 = 32 + 12 = 9 + 1 = 10.

    Do đó AD=10cm.

    Áp dụng định lí Pythagore cho DAHC vuông tại H, ta có:

    AC2 = AH2 + HC2 = 32 + 22 = 9 + 4 = 13.

    Do đó AC=13cm.

    Vậy AD=BC=10  cm,AC=BD=13  cm.

    Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác: 

    Khởi động trang 68 Toán 8 Tập 1: Mái ngói của trụ sở Ủy ban nhân dân Thành phố Hồ Chí Minh có hình dạng một tứ giác ABCD...

    Khám phá 1 trang 68 Toán 8 Tập 1: Tứ giác ABCD (Hình 1b) là hình vẽ minh hoạ một phần của chiếc thang ở Hình la. Nêu nhận xét của em về hai cạnh AB và CD của tứ giác này...

    Thực hành 1 trang 69 Toán 8 Tập 1: Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em...

    Vận dụng 1 trang 69 Toán 8 Tập 1: Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân ABCD (Hình 4). Cho biết D^=C^=75°...

    Vận dụng 2 trang 69 Toán 8 Tập 1: Tứ giác EFGH có các góc cho như trong Hình 5.

    a) Chứng minh rằng EFGH là hình thang...

    Khám phá 2 trang 69 Toán 8 Tập 1: a) Cho hình thang cân ABCD có hai đáy là AB và CD (AB > CD). Qua C vẽ đường thẳng song song với AD và cắt AB tại E (Hình 6a)...

    Thực hành 2 trang 70 Toán 8 Tập 1: Tìm các đoạn thẳng bằng nhau trong hình thang cân MNPQ có hai đáy là MN và PQ...

    Vận dụng 3 trang 70 Toán 8 Tập 1: Một khung cửa sổ hình thang cân có chiều cao 3 m, hai đáy là 3 m và 1 m (Hình 9)...

    Khám phá 3 trang 70 Toán 8 Tập 1: Cho hình thang ABCD có hai đáy là AB, CD và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua C, song song với BD và cắt AB tại E...

    Thực hành 3 trang 71 Toán 8 Tập 1: Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12...

    Vận dụng 4 trang 71 Toán 8 Tập 1: Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm...

    Bài 1 trang 71 Toán 8 Tập 1: Tìm x và y ở các hình sau...

    Bài 2 trang 71 Toán 8 Tập 1: Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang...

    Bài 3 trang 72 Toán 8 Tập 1: Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH và cắt AB tại N...

    Bài 4 trang 72 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA...

    Bài 5 trang 72 Toán 8 Tập 1: Tứ giác nào trong Hình 15 là hình thang cân...

    Bài 6 trang 72 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB và cắt AD, BC lần lượt tại F và G (Hình 16)...

    Bài 7 trang 72 Toán 8 Tập 1: Mặt bên của một chiếc va li (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b...

    Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 2: Tứ giác

    Bài 3: Hình thang – Hình thang cân

    Bài 4: Hình bình hành – Hình thoi

    Bài 5: Hình chữ nhật – Hình vuông

    Bài tập cuối chương 3

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 686 23/04/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: