Giải Toán 11 trang 53 Tập 2 Kết nối tri thức

Với giải bài tập Toán 11 trang 53 Tập 2 trong Bài 25: Hai mặt phẳng vuông góc sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 53 Tập 2.

1 349 30/11/2023

Trang trước

Trang sau

Giải Toán 11 trang 53 Tập 2

Bài 7.16 trang 53 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H là hình chiếu của A trên BC.

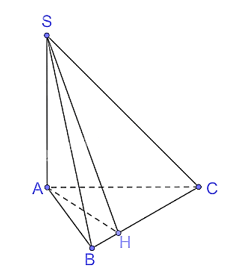
a) Chứng minh rằng (SAB) ⊥ (ABC) và (SAH) ⊥ (SBC).

b) Giả sử tam giác ABC vuông tại A, $\hat{A B C} = 30 °$ , AC = a, $S A = \frac{a \sqrt{3}}{2}$ . Tính số đo của góc nhị diện [S, BC, A].

Lời giải:

Giải Toán 11 trang 53 Tập 2 Kết nối tri thức

a) Vì SA ⊥ (ABC) nên (SAB) ⊥ (ABC).

Vì SA ⊥ (ABC) nên SA ⊥ BC.

Vì H là hình chiếu của A trên BC nên AH ⊥ BC.

Vì SA ⊥ BC và AH ⊥ BC nên BC ⊥ (SAH), suy ra (SAH) ⊥ (SBC).

b) Vì BC ⊥ (SAH) nên BC ⊥ SH mà AH ⊥ BC nên $\hat{S H A}$ là góc phẳng nhị diện của góc nhị diện [S, BC, A].

Xét tam giác ABC vuông tại A, $\hat{A B C} = 30 °$ , AC = a có: $\tan \hat{A B C} = \frac{A C}{A B}$

$\Rightarrow A B = \frac{A C}{\tan \hat{A B C}} = \frac{a}{\tan 30 °} = a \sqrt{3}$ .

Xét tam giác ABC vuông tại A, có $\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}} = \frac{1}{3 a^{2}} + \frac{1}{a^{2}} = \frac{4}{3 a^{2}}$

$\Rightarrow A H = \frac{a \sqrt{3}}{2}$ .

Vì SA ⊥ (ABC) nên SA ⊥ AH.

Xét tam giác SAH vuông tại A có: $\tan \hat{S H A} = \frac{S A}{A H} = \frac{\frac{a \sqrt{3}}{2}}{\frac{a \sqrt{3}}{2}} = 1$ $\Rightarrow \hat{S H A} = 45 °$ .

Vậy số đo của góc nhị diện [S, BC, A] bằng 45°.

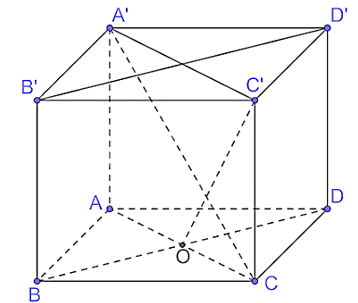
Bài 7.17 trang 53 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.

a) Tính độ dài đường chéo của hình lập phương.

b) Chứng minh rằng (ACC'A') ⊥ (BDD'B').

c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng $\hat{C O C^{'}}$ là một góc phẳng của góc nhị diện [C, BD, C']. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C'], [A, BD,C'].

Lời giải:

Giải Toán 11 trang 53 Tập 2 Kết nối tri thức

a) Vì ABCD.A'B'C'D' là hình lập phương nên có các mặt là hình vuông.

Xét tam giác ABC vuông tại B, có $A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ .

Vì AA' ⊥ (ABCD) nên AA' ⊥ AC.

Xét tam giác A'AC vuông tại A, có $A^{'} C = \sqrt{A {A^{'}}^{2} + A C^{2}} = \sqrt{a^{2} + 2 a^{2}} = a \sqrt{3}$ .

Vậy đường chéo của hình lập phương có độ dài là $a \sqrt{3}$ .

b) Vì AA' ⊥ (ABCD) nên AA' ⊥ BD.

Vì ABCD là hình vuông nên AC ⊥ BD mà AA' ⊥ BD, suy ra BD ⊥ (ACC'A').

Vì BD ⊥ (ACC'A') nên (ACC'A') ⊥ (BDD'B').

c) Vì BD ⊥ (ACC'A') nên BD ⊥ C'O mà CO ⊥ BD (do AC ⊥ BD) nên $\hat{C O C^{'}}$ là góc phẳng nhị diện của góc nhị diện [C, BD, C'].

Do ABCD là hình vuông nên O là trung điểm của AC, suy ra $A O = O C = \frac{A C}{2} = \frac{a \sqrt{2}}{2}$ .

Xét tam giác C'CO vuông tại C, có $\tan \hat{C^{'} O C} = \frac{C C^{'}}{C O} = \frac{a}{\frac{a \sqrt{2}}{2}} = \sqrt{2}$ $\Rightarrow \hat{C^{'} O C} \approx 55 °$ .

Vậy số đo của các góc nhị diện [C, BD, C'] khoảng 55°.

Vì AO ⊥ BD (do AC ⊥ BD), BD ⊥ C'O nên $\hat{A O C^{'}}$ là góc phẳng nhị diện của góc nhị diện [A, BD,C'].

Vì $\hat{A O C^{'}} + \hat{C^{'} O C} = 180 °$ nên $\hat{A O C^{'}} = 180 ° - \hat{C^{'} O C} \approx 180 ° - 55 ° = 125 °$ .

Vậy số đo góc nhị diện [A, BD,C'] khoảng 125°.

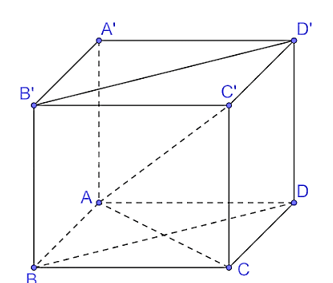
Bài 7.18 trang 53 Toán 11 Tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D'.

a) Chứng minh rằng (BDD'B') ⊥ (ABCD).

b) Xác định hình chiếu của AC' trên mặt phẳng (ABCD).

c) Cho AB = a, BC = b, CC' = c. Tính AC'.

Lời giải:

Giải Toán 11 trang 53 Tập 2 Kết nối tri thức

a) Vì ABCD.A'B'C'D' là hình hộp chữ nhật nên BB' ⊥ (ABCD).

Suy ra (BDD'B') ⊥ (ABCD).

b) Vì ABCD.A'B'C'D' là hình hộp chữ nhật nên CC' ⊥ (ABCD), suy ra C là hình chiếu của C' trên mặt phẳng (ABCD).

A là hình chiếu của A trên mặt phẳng (ABCD). Do đó AC là hình chiếu của AC' trên mặt phẳng (ABCD).

c) Vì ABCD là hình chữ nhật nên $A C^{2} = A B^{2} + B C^{2} = a^{2} + b^{2}$ .

Vì CC' ⊥ (ABCD) nên CC' ⊥ AC.

Xét tam giác C'CA vuông tại C, có $A C^{'} = \sqrt{A C^{2} + C {C^{'}}^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}$ .

Vậy $A C^{'} = \sqrt{a^{2} + b^{2} + c^{2}}$ .

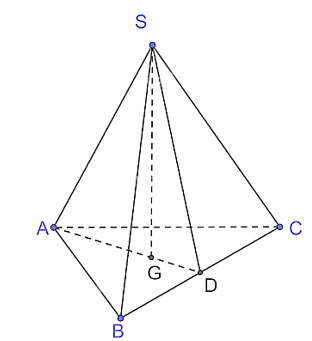
Bài 7.19 trang 53 Toán 11 Tập 2: Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.

a) Tính sin của góc tạo bởi cạnh bên và mặt đáy.

b) Tính tang của góc giữa mặt phẳng chứa mặt đáy và mặt phẳng chứa mặt bên.

Lời giải:

Giải Toán 11 trang 53 Tập 2 Kết nối tri thức

a) Gọi G là hình chiếu của S trên mặt phẳng (ABC).

Vì S.ABC đều nên G là tâm của tam giác ABC hay G là trọng tâm đồng thời G cũng là trực tâm của tam giác ABC.

Gọi a là góc tạo bởi cạnh bên SA và mặt phẳng đáy (ABC).

Vì SG ⊥ (ABC) nên GA là hình chiếu của SA trên mặt phẳng (ABC).

Khi đó góc giữa cạnh bên SA và mặt phẳng đáy (ABC) bằng góc giữa hai đường thẳng SA và AG. Mà (SA, AG) = $\hat{S A G} = α$ .

Kẻ AG cắt BC tại D, khi đó D là trung điểm của BC, AD ⊥ BC.

Xét tam giác ABC đều cạnh a, AD là đường cao nên $A D = \frac{a \sqrt{3}}{2}$ .

Suy ra $A G = \frac{2}{3} A D = \frac{2}{3} \cdot \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{3}$ .

Xét tam giác SGA vuông tại G, có $S G = \sqrt{S A^{2} - A G^{2}} = \sqrt{b^{2} - \frac{a^{2}}{3}}$ .

$\sin \hat{S A G} = \frac{S G}{S A} = \frac{\sqrt{b^{2} - \frac{a^{2}}{3}}}{b} = \sqrt{\frac{3 b^{2} - a^{2}}{3 b^{2}}} = \sqrt{1 - \frac{a^{2}}{3 b^{2}}}$ .

Vậy sin của góc tạo bởi cạnh bên và mặt đáy bằng $\sqrt{1 - \frac{a^{2}}{3 b^{2}}}$ .

b) Gọi $β$ là góc tạo bởi mặt phẳng (SBC) và (ABC).

Vì SG ⊥ (ABC) nên SG ⊥ BC mà AD ⊥ BC nên BC ⊥ (SAD), suy ra BC ⊥ SD.

Khi đó góc giữa hai mặt phẳng (SBC) và (ABC) bằng góc giữa hai đường thẳng AD và SD, mà (AD, SD) = $\hat{S D A} = β$ .

Vì $G D = \frac{1}{3} A D = \frac{1}{3} \cdot \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{6}$ .

Xét tam giác SGD vuông tại G, có

$\tan \hat{S D G} = \frac{S G}{G D} = \frac{\sqrt{b^{2} - \frac{a^{2}}{3}}}{\frac{a \sqrt{3}}{6}}$ $= \sqrt{\frac{36 (3 b^{2} - a^{2})}{9 a^{2}}}$ $= \sqrt{\frac{4 (3 b^{2} - a^{2})}{a^{2}}}$ $= \frac{2 \sqrt{3 b^{2} - a^{2}}}{a}$ .

Bài 7.20 trang 53 Toán 11 Tập 2: Hai mái nhà trong Hình 7.72 là hai hình chữ nhật. Giả sử AB = 4,8 m; OA = 2,8 m; OB = 4 m.

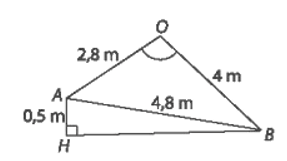
a) Tính (gần đúng) số đo của góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà.

b) Chứng minh rằng mặt phẳng (OAB) vuông góc với mặt đất phẳng. Lưu ý: Đường giao giữa hai mái (đường nóc) song song với mặt đất.

c) Điểm A ở độ cao (so với mặt đất) hơn điểm B là 0,5 m. Tính (gần đúng) góc giữa mái nhà (chứa OB) so với mặt đất.

Lời giải:

Giải Toán 11 trang 53 Tập 2 Kết nối tri thức

a) Vì hai mái nhà trong Hình 7.72 là hai hình chữ nhật nên góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà bằng góc giữa hai đường thẳng OA và OB, mà (OA, OB) = $\hat{A O B}$ .

Áp dụng định lí Côsin trong tam giác OAB, ta có:

$c o s \hat{A O B} = \frac{O A^{2} + O B^{2} - A B^{2}}{2 \cdot O A \cdot O B}$ $= \frac{2, 8^{2} + 4^{2} - 4, 8^{2}}{2 \cdot 2, 8 \cdot 4}$ $= \frac{1}{28}$ $\Rightarrow \hat{A O B} \approx 88 °$ .

Vậy số đo của góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà khoảng 88°.

b) Vì đường giao giữa hai mái nhà vuông góc với OA và OB nên đường giao giữa hai mái nhà vuông góc với mặt phẳng (OAB).

Mà đường giao giữa hai mái nhà song song với mặt đất nên mặt phẳng (OAB) vuông góc với mặt đất phẳng.

c) Gọi H là giao điểm của đường thẳng qua B và song song với mặt đất với đường thẳng đi qua A và vuông góc với mặt đất.

Khi đó góc giữa mái nhà chứa OB và mặt đất là góc OBH.

Xét tam giác AHB vuông tại H, có: $\sin \hat{A B H} = \frac{A H}{A B} = \frac{0, 5}{4, 8} = \frac{5}{48}$ $\Rightarrow \hat{A B H} \approx 6 °$ .

Áp dụng định lí Côsin trong tam giác OAB có:

$c o s \hat{O B A} = \frac{O B^{2} + A B^{2} - O A^{2}}{2 \cdot O B \cdot A B} = \frac{4^{2} + 4, 8^{2} - 2, 8^{2}}{2 \cdot 4 \cdot 4, 8} = \frac{13}{16} \Rightarrow \hat{O B A} \approx 36 °$ .

Do đó $\hat{O B H} = \hat{O B A} + \hat{A B H} \approx 36 ° + 6 ° = 42 °$ .

Vậy góc giữa mái nhà (chứa OB) so với mặt đất khoảng 42°.

Bài 7.21 trang 53 Toán 11 Tập 2: Độ dốc của mái nhà, mặt sân, con đường thẳng là tang của góc tạo bởi mái nhà, mặt sân, con đường thẳng đó với mặt phẳng nằm ngang. Độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá $\frac{1}{12}$ . Hỏi theo đó, góc tạo bởi đường dành cho người khuyết tật và mặt phẳng nằm ngang không vượt quá bao nhiêu độ? (Làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải:

Gọi $α$ là góc tạo bởi đường dành cho người khuyết tật và mặt phẳng nằm ngang.

Vì độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá $\frac{1}{12}$ nên $\tan α \leq \frac{1}{12} \Rightarrow α \leq 4, 76 °$ .