Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 40 Tập 1 | Kết nối tri thức Giải Toán lớp 10

    Với giải bài tập Toán lớp 10 trang 40 Tập 1 trong Bài 6: Hệ thức lượng trong tam giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 40 Tập 1.

    1 482 03/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 40 Tập 1

    Luyện tập 2 trang 40 Toán 10 Tập 1: Cho tam giác ABC có b = 8, c = 5 và B^=80o. Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.

    Lời giải:

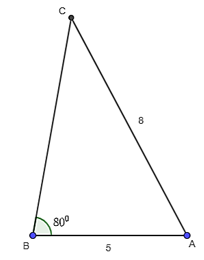
    Cho tam giác ABC có b = 8, c = 5 và góc B = 80 độ Tính số đo các góc (ảnh 1)

    Áp dụng định lý sin cho ΔABC, ta có:

    asinA=bsinB=csinC=2R

    sinC=c . sinBb=5 . sin80o8≈0,6155

    ⇔C^≈38o.

    Lại có A^+B^+C^=180o

    ⇔A^=180o−B^−C^

    ⇔A^≈180°−80°−38°=62°.

    Theo định lí sin, ta suy ra:

    a=sinA . bsinB=sin62o . 8sin80o≈7,17

    Và 2R=bsinB⇒R=b2 sinB=82 sin80o≈4,062.

    Vậy a ≈ 7,17; R ≈ 4,062; A^≈62°;  C^≈38°.

    3. Giải tam giác và ứng dụng thực tế

    Luyện tập 3 trang 40 Toán 10 Tập 1: Giải tam giác ABC, biết b = 32, c = 45;A^=87o.

    Lời giải:

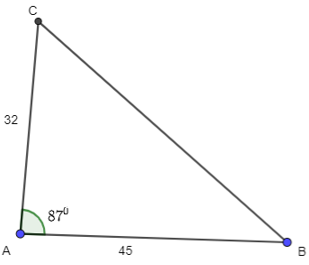
    Giải tam giác ABC, biết b = 32, c = 45 (ảnh 1)

    Áp dụng định lý cosin tại đỉnh A, ta có:

    a2 = b2 + c2 − 2bc . cosA

    ⇒ BC2 = AB2 + AC2 – 2 . AB . AC . cosA

    ⇒ BC2 = 322 + 452 – 2 . 32 . 45 . cos 87o

    ⇒ BC2 ≈ 2898,27

    ⇒ BC ≈ 53,84.

    Theo định lí sin, ta có: asinA=bsinB

    ⇒sinB=b . sinAa=32 . sin87o53,8≈0,594

    ⇒B^≈36,44o hoặc B^≈143,56o (loại vì A^+B^≈230,56o>180o).

    Ta có: A^+B^+C^=180o

    ⇒C^=180o−A^−B^

    ⇒C^≈180o−87o−36,44o=56,56o.

    Vậy BC = 53,84; B^=36,44o;  C^=56,56o.

    Vận dụng 2 trang 40 Toán 10 Tập 1: Từ một khu vực có thể quan sát hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.

    Lời giải:

    Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.

    Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó.

    Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.

    * Tính AB bằng cách:

    + Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc α.

    + Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là góc β.

    Ta có hình vẽ:

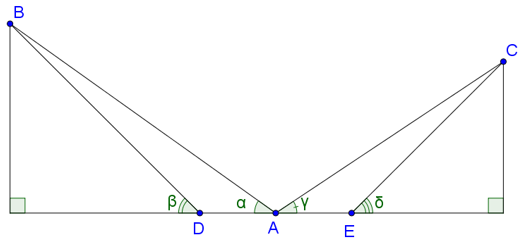
    Từ một khu vực có thể quan sát hai đỉnh núi, ta có thể ngắm và đo để xác định (ảnh 1)

    Ta có: ADB^=180o−β; DBA^=β−α.

    Áp dụng định lí sin vào ∆ABD, ta được: ABsinADB^=DAsinDBA^

    ⇒AB=sinADB^ .DAsinDBA^

    ⇒AB=sin(180°−β) .DAsin(β−α).

    * Tương tự ngắm và đo để xác định AC.

    Ta có: AEC^=180o−δ; ACE^=δ−γ.

    Áp dụng định lí sin vào ∆ACE, ta được: ACsinAEC^=AEsinACE^

    ⇒AC=sinAEC^  .  AEsinACE^

    ⇒AC=sin(180o−δ) .AEsin(δ−γ).

    Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí côsin cho tam giác ABC để tính độ dài cạnh BC.

    Ta có: BC2 = AB2 + AC2 – 2AB.AC.cosBAC.

    Với AB, AC, góc BAC đã biết ở các bước trên, thay vào ta tính được BC chính là khoảng cách giữa hai đỉnh núi.

    Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Giải Toán 10 trang 38 Tập 1

    Giải Toán 10 trang 39 Tập 1

    Giải Toán 10 trang 41 Tập 1

    Giải Toán 10 trang 42 Tập 1

    Giải Toán 10 trang 43 Tập 1

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 482 03/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: