Giải SBT Toán 6 Bài 5 (Cánh diều): Phép nhân các số nguyên

Mục lục Giải SBT Toán 6 Bài 5: Phép nhân các số nguyên

Bài 40 trang 81 SBT Toán 6 Tập 1: Thực hiện phép tính:

a) (-6).9;

b) (-12).(-987);

c) 90.(-108).(-3);

d) 29.(-78).(-9).(-11);

e) 6.(-4)².(-10)² + 5²;

f) (-7).(-7).(-7) + 7³;

h) (-10³).(-10²) – 13²;

i) (-8).(-8).(-8).(-8) – 8⁴ + 10⁵.

Lời giải

a) (-6).9

= -6.9

= -54.

b) (-12).(-987)

= 12.987

= 11 844.

c) 90.(-108).(-3)

= (-9 720).(-3)

= 29 160.

d) 29.(-78).(-9).(-11)

= (-2 262).(-9).(-11)

= 20 358.(-11)

= - 223 938.

e) 6.(-4)².(-10)² + 5²

= 6.16.100 + 25

= 9 600 + 25

= 9 625.

f) (-7).(-7).(-7) + 7³

= - 7³ + 7³

= 7³ – 7³

= 0.

h) (-10³).(-10²) – 13²

= (-1 000).(-100) – 169

= 100 000 – 169

= 99 831.

i) (-8).(-8).(-8).(-8) – 8⁴ + 10⁵

= 8⁴ – 8⁴ + 10⁵

= 0 + 10⁵

= 10⁵.

Bài 41 trang 82 SBT Toán 6 Tập 1:

Chọn các dấu “+”, “-“ thích hợp cho $\boxed{?}$:

a	b	Dấu của a.b
+	-	?
-	+	?
-	-	?
+	+	?

Lời giải

+) a mang dấu dương, b mang dấu âm suy ra a và b là hai số nguyên trái dấu. Do đó tích a.b mang dấu âm.

+) a mang dấu âm, b mang dấu dương suy ra a và b là hai số nguyên trái dấu. Do đó tích a.b mang dấu âm.

+) a mang dấu âm, b mang dấu âm suy ra a và b là hai số nguyên cùng dấu. Do đó tích a.b mang dấu dương.

+) a mang dấu dương, b mang dấu dương suy ra a và b là hai số nguyên cùng dấu. Do đó tích a.b mang dấu dương.

Khi đó ta có bảng sau:

a	b	Dấu của a.b
+	-	-
-	+	-
-	-	+
+	+	+

Bài 42 trang 82 SBT Toán 6 Tập 1:

Chọn số thích hợp cho $\boxed{?}$:

a	-23	221	?	-25	12
b	-9	-45	399	?	?
c	2	?	0	-1	-38
a.b	?	?	1 197	-100	-156
c(a + b)	?	176	?	?	?

Lời giải

+) Với a = -23, b = -9, c = 2 thì:

a.b = (-23).(-9) = 207;

c(a + b) = 2.[(-23) + (-9)] = 2.(-32) = -64.

+) Với a = 221, b = -45, c(a + b) = 176 thì:

a.b = 221.(-45) = -9 945;

Ta có: c(a + b) = 176

c.[221 + (-45)] = 176

c.176 = 176

c = 1.

+) Với b = 399, c = 0, a.b = 1 197. Khi đó:

Ta có: a.b = 1 197

a.399 = 1 197

a = 1 197:399

a = 3;

c.(a + b) = 0.(399 + 3) = 0.402 = 0.

+) Với a = -25, c = -1 và a.b = -100. Khi đó:

Ta có: a.b = -100

(-25).b = -100

(-25).b = (-25).4

b = 4.

c(a + b) = (-1).[(-25) + 4] = (-1).(-21) = 21.

+) Với a = 12, c = -38, a.b = -156. Khi đó:

Ta có: a.b = -156

12.b = -156

12.b = 12.(-13)

b = -13;

c(a + b) = (-38).[12 + (-13)] = (-38).(-1) = 38.

Từ đó, ta có bảng sau:

a	-23	221	3	-25	12
b	-9	-45	399	4	-13
c	2	1	0	-1	-38
a.b	207	-9 945	1 197	-100	-156
c(a + b)	-64	176	0	21	38

Bài 43 trang 82 SBT Toán 6 Tập 1:

Tính giá trị của biểu thức trong mỗi trường hợp sau:

a) 19x với x = - 7;

b) 28xy với x = -12 và y = -15;

c) 29m – 58n với m = -2 và n = 3;

d) (- 2021)abc + ab với a = -21, b = -11 và c = 0.

Lời giải

a) Thay x = -7 vào 19x, ta được:

19.(-7) = -133.

Vậy với x = -7 thì giá trị biểu thức là -133.

b) Thay x = -12 và y = -15 vào biểu thức 28xy, ta được:

28.(-12).(-15) = (-336).(-15) = 5 040.

Vậy với x = -12 và y = -15 thì giá trị biểu thức là 5 040.

c) Thay m = -2 và n = 3 vào 29m – 58n, ta được:

29.(-2) – 58.3

= (-58) – 58.3

= (-58) + (-58).3

= (-58).(1 + 3)

= (-58).4

= -232.

Vậy với m = -2 và n = 3 thì giá trị biểu thức là -232.

d) Thay a = -21, b = -11 và c = 0 vào biểu thức (- 2021)abc + ab, ta được:

(- 2021)(-21).(-11).0 + (-21).(-11)

= 0 + 231

= 231.

Vậy với a = -21, b = -11 và c = 0 thì giá trị biểu thức là 231.

Bài 44 trang 82 SBT Toán 6 Tập 1:

Chọn dấu “<”, “>”, “=” thích hợp cho dấu $\boxed{?}$:

a) $\left(-76\right)\left(-2\right)\boxed{?}76.2;$

b) $\left(-4098\right).0\boxed{?}98;$

c) $-144\boxed{?}12.\left(-12\right).11;$

d) $432.37.32\boxed{?}\left(-432\right).37.\left(-32\right);$

e) $4138.\left(-12\right).6171\boxed{?}0;$

g) $\left(-98\right).54.\left(-33\right).9\boxed{?}\left(-98\right).54.33.9.$

Lời giải

a) Ta có (-76).(-2) = 76.2.

Do đó ta điền: $\left(-76\right)\left(-2\right)\boxed{=}76.2;$

b) Ta có (-4 098).0 = 0 < 98.

Do đó ta điền: $\left(-4098\right).0\boxed{<}98;$

c) Ta có 12.(-12).11 = (-144).11 = -1 584 < -144.

Do đó ta điền: $-144\boxed{>}12.\left(-12\right).11;$

d) Ta có: (-432).37.(-32) =-(432.37).(-32) = 432.37.32.

Do đó ta điền: $432.37.32\boxed{=}\left(-432\right).37.\left(-32\right);$

e) 4 138.(-12).6 171 = -(4 138.12).6 171 = -(4 138.12.6 171) < 0.

Do đó ta điền: $4138.\left(-12\right).6171\boxed{<}0;$

g) Ta có: (-98).54.(-33).9 = 98.54.33.9, (-98).54.33.9 = -(98.54.33.9).

Vì -(98.54.33.9) < 98.54.33.9 nên (-98).54.33.9 < (-98).54.(-33).9.

Do đó ta điền: $\left(-98\right).54.\left(-33\right).9\boxed{>}\left(-98\right).54.33.9.$

Bài 45 trang 82 SBT Toán 6 Tập 1:

Tính một cách hợp lí:

a) (-16).(-9).5;

b) (-15).999;

c) (-25).144.(-4);

d) (-125).2 020.(-8);

e) (-2 021).(-15) + (-15).2 020;

g) 121.(-63) + 63.(-53) – 63.26.

Lời giải

a) (-16).(-9).5

= [(-16).5].(-9)

= (-80).(-9)

= 720.

b) (-15).999

= (-15)(1 000 – 1)

= (-15).1 000 – (-15).1

= -15 000 + 15

= -(15 000 – 15)

= -14 985.

c) (-25).144.(-4)

= [(-25).(-4)].144

= 100.144

= 14 400.

d) (-125).2 020.(-8)

= [(-125).(-8)].2 020

= 1 000.2 020

= 2 020 000.

e) (-2 021).(-15) + (-15).2 020

= (-15).[(-2 021) + 2 020]

= (-15).(-1)

= 15.

g) 121.(-63) + 63.(-53) – 63.26

= 121.(-63) + (-63).53 + (-63).26

= (-63).(121 + 53 + 26)

= (-63).200

= -12 600.

Bài 46 trang 83 SBT Toán 6 Tập 1:

Báo cáo kinh doanh trong 6 tháng đầu năm của công ty Bình An được thống kê như sau:

Tháng	Lợi nhuận (triệu đồng)
Tháng 1	50
Tháng 2	-10
Tháng 3	50
Tháng 4	40
Tháng 5	-20
Tháng 6	-10

Sau 6 tháng đầu năm, công ty Bình An kinh doanh lãi hay lỗ với số tiền là bao nhiêu?

Lời giải

Số tiền của công ty Bình An thu được sau 6 tháng đầu năm là:

50 + (-10) + 50 + 40 + (-20) + (-10) = 100 (triệu đồng)

Vậy sau 6 tháng đầu năm, công tu Bình An kinh doanh lãi 100 triệu đồng.

Bài 47 trang 83 SBT Toán 6 Tập 1:

So sánh hai biểu thức sau mà không tính cụ thể giá trị của chúng:

a) (- 2021).2 021 và (-2 020).2 022;

b) (8 765 – 5 678).[5 678 – 9 765 + (-12)] và 4 342.

Lời giải

a) Ta có: (- 2021).2 021

= [(-2 020) + (-1)].2 021

= (-2 020).2 021 + (-1).2 021

= (-2 020).2 021 + (-2 021)

Ta có: (-2 020).2 022 = (-2 020)(2 021 + 1) = (-2 020).2 021 + (-2 020).

Vì -2 021 < -2 020

Nên (-2 020).2 021 + (-2 021) < (-2 020).2 021 + (-2 020)

Hay (- 2021).2 021 < (-2 020).2 022.

b) (8 765 – 5 678).[5 678 – 9 765 + (-12)] và 4 342.

Ta có 8 765 – 5 678 > 0, 5 678 – 9 765 + (-12) < 0.

Do đó (8 765 – 5 678).[5 678 – 9 765 + (-12)] < 0 mà 4 342 > 0.

Vậy (8 765 – 5 678).[5 678 – 9 765 + (-12)] < 4 342.

Bài 48 trang 83 SBT Toán 6 Tập 1:

Cho hai số nguyên x, y

$\left(\mathrm{x}\ne 0,\mathrm{y}\ne 0,\mathrm{x}>\mathrm{y},\mathrm{x}\ne -\mathrm{y}\right).$

Gọi m = x².y².(x – y).(x + y)⁴. Hỏi m là số nguyên dương hay nguyên âm?

Lời giải

Vì x > y nên x – y > 0.

Ta có x² $\ge$ 0 với mọi x mà x $\ne$ 0 nên x² > 0.

Ta có y² $\ge$ 0 với mọi x mà y $\ne$ 0 nên y² > 0.

Ta lại có x $\ne$ - y nên x + y $\ne$ 0 suy ra (x + y)⁴ > 0.

Do đó m = x².y².(x – y).(x + y)⁴ > 0.

Vậy m là một số nguyên dương.

Bài 49 trang 83 SBT Toán 6 Tập 1:

Tìm các số nguyên x thỏa mãn:

a) 16x² = 64;

b) 25(x² – 1) – 75 = 9 900;

c) (x – 6).(2x – 6) = 0;

d) (5x – 10)(6x + 12) = 0.

Lời giải

a) 16x² = 64

x² = 64:16

x² = 4

x² = 2² = (-2)²

x = 2 hoặc x = -2.

Vậy x = 2 hoặc x = -2.

b) 25(x² – 1) – 75 = 9 900

25(x² – 1) = 9 900 + 75

25(x² – 1) = 9 975

x² – 1 = 9 975:25

x² – 1 = 9 975:25

x² – 1 = 399

x² = 400

x² = 20² = (-20)²

x = 20 hoặc x = -20.

Vậy x = 20 hoặc x = -20.

c) (x – 6).(2x – 6) = 0

TH1: x – 6 = 0

x = 6.

TH2: 2x – 6 = 0

2x = 6

x = 3.

Vậy x = 6 hoặc x = 3.

d) (5x – 10)(6x + 12) = 0

TH1: 5x – 10 = 0

5x = 10

x = 2.

TH2: 6x + 12 = 0

6x = -12

6x = 6.(-2)

x = -2.

Vậy x = 2 hoặc x = -2.

Bài 50 trang 83 SBT Toán 6 Tập 1:

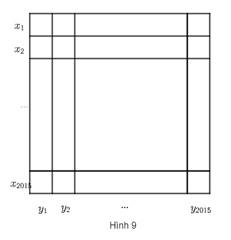
Cho bảng gồm 2 015x2 015 ô vuông nhỏ (Hình 9).

Điền vào mỗi ô của bảng số 1 hoặc số -1.

Bên trái mỗi dòng thứ i ghi tích các số của dòng đó và đặt là x_i. Dưới mỗi cột thứ j ghi tích các số của cột đó và đặt là y_j (i = 1; 2; 3; …; 2 015 và j = 1; 2; 3; …; 2 015).

Chứng tỏ rằng tổng của 4 030 số x_i,y_j nhận được khác 0.

Lời giải

Giả sử tổng của 4 030 số x_i,y_j bằng 0.

Ta có x₁ + x₂ + … + x₂₀₁₅ + y₁ + y₂ + … + y₂₀₁₅ = 0.

Mà mỗi số x_i, y_i đều bằng 1 hoặc -1 nên trong 4 030 số x_i, y_i có 2 015 số bằng -1 và 2 015 số bằng 1.

Do đó tích x₁.x₂…x₂₀₁₅.y₁.y₂…y₂₀₁₅ = - 1 (vì số các thừa số bằng -1 là lẻ) (1)

Mặt khác x₁.x₂…x₂₀₁₅ = y₁.y₂…y₂₀₁₅ (đều là tích của các số trong bảng).

Suy ra x₁.x₂…x₂₀₁₅.y₁.y₂…y₂₀₁₅ = (x₁.x₂…x₂₀₁₅)² = 1 (mâu thuẫn với (1)).

Do đó giải sử sai.

Vậy tổng của 4 030 số x_i,y_j nhận được khác 0.

Xem thêm lời giải sách bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:

Bài 6: Phép chia hết hai số nguyên. Quan hệ chia hết trong tập hợp số nguyên

Bài ôn tập cuối chương 2

Bài 1: Tam giác đều. Hình vuông. Lục giác đều

Bài 2: Hình chữ nhật. Hình thoi

Bài 3: Hình bình hành