Giải SBT Toán 6 Bài 11 (Cánh diều): Phân tích một số ra thừa số nguyên tố
Lời giải sách bài tập Toán lớp 6 Bài 11: Phân tích một số ra thừa số nguyên tố sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong sách bài tập Toán 6.
Mục lục Giải SBT Toán 6 Bài 11: Phân tích một số ra thừa số nguyên tố
Bài 99 trang 31 SBT Toán 6 Tập 1:
Phân tích các số sau ra thừa số nguyên tố: 16; 23; 120; 625.
Lời giải
+) Ta có:
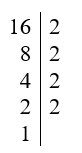
Vậy 16 = 24.
+) Ta có:
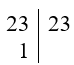
Vậy 23 = 23.
+) Ta có:
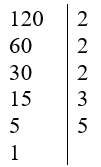
Vậy 120 = 23.3.5.
+) Ta có:
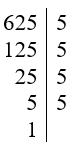
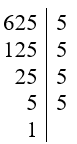
Vậy 625 = 54.
Bài 100 trang 31 SBT Toán 6 Tập 1:
Thực hiện mỗi phép tính sau, rồi phân tích kết quả ra thừa số nguyên tố:
Lời giải
a) 777:7 + 361:192
= 777:7 + 361:361
= 111 + 1
= 112.
Ta có:
Vậy 112 = 24.7.
b) 3.52 – 3.17 + 43.7
= 3.25 – 3.17 + 64.7
= 75 – 51 + 448
= 472
Ta có:
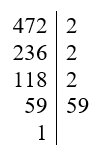
Vậy 472 = 23.59.
Bài 101 trang 31 SBT Toán 6 Tập 1:
Lời giải
Ta có:
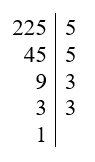
Vậy 225 = 32.52.
Suy ra 225 chia hết cho các số nguyên tố là 3 và 5.
Ta có:

Vậy 1 200 = 24.3.52.
Suy ra 1 200 chia hết cho các số nguyên tố là 2, 3 và 5.
Bài 102 trang 31 SBT Toán 6 Tập 1:
Lời giải
Cách 1.
Ta có a = p.q2 nên tập các Ư(a) = {1; p; q; q2; pq; pq2}.
Do đó a có 6 ước là đúng.
Cách 2.
Nếu a = pm.qn thì số ước của a là: (m + 1).(n + 1).
Áp dụng vào bài toán, ta có a = p.q2 khi đó a có (1 + 1)(2 + 1) = 2.3 = 6. Vậy a có tất cả 6 ước là đúng.
Bài 103 trang 31 SBT Toán 6 Tập 1:
Cho a = 72.113. Trong các số 7a, 11a, 13a, số nào có nhiều ước nhất?
Lời giải
Ta có: 7a = 7. 72.113 = 73.113.
Suy ra 7a có tất cả (3 + 1).(3 + 1) = 4.4 = 16 ước.
Ta có: 11a = 11.72.113 = 72.114.
Suy ra 11a có tất cả (2 + 1).(4 + 1) = 3.5 = 15 ước.
Ta có: 13a = 13.72.113.
Suy ra 13a có tất cả (2 + 1).(3 + 1).(1 + 1) = 3.4.2 = 24 ước.
Vậy số 13a là số nhiều ước nhất.
Bài 104 trang 31 SBT Toán 6 Tập 1:
a) 2 + 4 + 6 + … + 2.(n – 1) + 2n = 210.
b) 1 + 3 + 5 + … + (2n – 3) + (2n – 1) = 225.
Lời giải
a) Số số hạng của VT là:
(2n – 2):2 + 1 = n – 1 + 1 = n số.
Khi đó: 2 + 4 + 6 + … + 2.(n – 1) + 2n = (2n + 2).n:2 = n.(n+1).
Theo đầu bài, ta có: n(n + 1) = 210
Ta có:
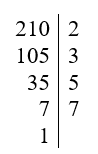
Suy ra 210 = 2.3.4.5= 14.15.
Vậy n = 14.
b) Số số hạng của VT là:
(2n – 1 – 1):2 + 1 = (2n – 2):2 + 1 = n – 1 + 1 = n.
Khi đó 1 + 3 + 5 + … + (2n – 3) + (2n – 1) = (2n – 1 + 1).n:2 = 2n.n:2 = n2.
Ta có 223 = 32.52 = 152.
Vậy n = 15.
Bài 105 trang 32 SBT Toán 6 Tập 1:
Lời giải
Vì để xếp 16 cái bút vào các hộp sao cho số bút của các hộp bằng nhau nên số hộp bút là ước của 16.
Ta có: 16 = 24 nên các ước của 16 là: 1; 2; 4; 8; 16.
Ta có bảng sau:
|
Số hộp bút |
Số bút trong mỗi hộp |
|
1 |
16 |
|
2 |
8 |
|
4 |
4 |
|
8 |
2 |
|
16 |
1 |
Vì mỗi hộp có ít nhất hai cái bút nên ta loại trường hợp chia thành 16 hộp bút.
Vậy bạn Khanh có thể xếp số bút đó vào 1 hộp, 2 hộp, 4 hộp hoặc 8 hộp.
Bài 106 trang 32 SBT Toán 6 Tập 1:
Lời giải
Xếp 1 015 học sinh thành các hàng sao cho số học sinh mỗi hàng là như nhau nên số hàng là ước của 1 015.
Ta có: 1 015 = 5.7.29.
Ta có bảng sau:
|
Số hàng |
Số học sinh mỗi hàng |
|
1 |
1 015 |
|
5 |
203 |
|
7 |
145 |
|
29 |
35 |
|
35 |
29 |
|
145 |
7 |
|
203 |
5 |
|
1 015 |
1 |
Vì số hàng không quá 40 hàng và không ít hơn 10 hàng nên ta có thể xếp 1 015 thành 29 hàng hoặc 35 hàng.
Bài 106 trang 32 SBT Toán 6 Tập 1:
Lời giải
Xếp 1 015 học sinh thành các hàng sao cho số học sinh mỗi hàng là như nhau nên số hàng là ước của 1 015.
Ta có: 1 015 = 5.7.29.
Ta có bảng sau:
|
Số hàng |
Số học sinh mỗi hàng |
|
1 |
1 015 |
|
5 |
203 |
|
7 |
145 |
|
29 |
35 |
|
35 |
29 |
|
145 |
7 |
|
203 |
5 |
|
1 015 |
1 |
Vì số hàng không quá 40 hàng và không ít hơn 10 hàng nên ta có thể xếp 1 015 thành 29 hàng hoặc 35 hàng.
Bài 108 trang 32 SBT Toán 6 Tập 1:
a) 3n + 13 chia hết cho n + 1;
b) 5n + 19 chia hết cho 2n + 1.
Lời giải
a) Ta có: 3n + 13 = 3n + 3 + 10 = 3.(n + 1) + 10.
Vì 3.(n + 1) chia hết cho n + 1 nên để 3n + 13 chia hết cho n + 1 thì 10 phải chia hết cho n + 1 hay n + 1 là ước của 10.
Ta có: 10 = 2.5 nên các ước của 10 là:
Ư(10) = {1; 2; 5; 10}.
Ta có bảng sau:
|
n + 1 |
1 |
2 |
5 |
10 |
|
n |
0 |
1 |
4 |
9 |
Vậy n {0; 1; 4; 9}.
b) 5n + 19 chia hết cho 2n + 1.
Vì 5n + 19 chia hết cho 2n + 1 nên 2(5n + 19) chia hết cho 2n + 1
Xét 2(5n + 19) = 10n + 38
= 10n + 5 + 33 = 5(2n + 1) + 33.
Vì 5.(2n + 1) chia hết cho 2n + 1 nên để 2(5n + 19) chia hết cho 2n + 1 thì 33 phải chia hết cho 2n + 1 hay 2n + 1 thuộc ước của 33.
Ta có bảng sau:
|
2n + 1 |
1 |
3 |
11 |
33 |
|
n |
0 |
1 |
5 |
16 |
Vậy n {0; 1; 5; 16}.
Xem thêm lời giải sách bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Bài 12: Ước chung và ước chung lớn nhất
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Cánh diều
- Soạn văn lớp 6 (ngắn nhất) - Cánh diều
- Bố cục tác phẩm Ngữ văn 6 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Văn mẫu lớp 6 – Cánh Diều
- Giải VBT Luyện viết Ngữ văn lớp 6 – Cánh diều
- Giải sgk Lịch Sử 6 – Cánh Diều
- Giải sbt Lịch Sử 6 – Cánh Diều
- Giải VBT Lịch sử 6 – Cánh diều
- Lý thuyết Lịch sử lớp 6 – Cánh diều
- Giải sbt Địa Lí 6 – Cánh Diều
- Giải sgk Địa Lí 6 – Cánh Diều
- Lý thuyết Địa Lí 6 – Cánh Diều
- Giải VBT Địa lí 6 – Cánh diều
- Giải sgk GDCD 6 – Cánh Diều
- Lý thuyết GDCD 6 – Cánh diều
- Giải sbt Giáo dục công dân 6 – Cánh diều
- Giải sgk Công nghệ 6 – Cánh Diều
- Lý thuyết Công nghệ 6 – Cánh Diều
- Giải sgk Khoa học tự nhiên 6 – Cánh Diều
- Giải sbt Khoa học tự nhiên 6 – Cánh Diều
- Lý thuyết Khoa học tự nhiên 6 – Cánh Diều
- Giải sgk Tin học 6 – Cánh Diều
- Lý thuyết Tin học 6 – Cánh Diều
- Giải sgk Tiếng Anh 6 - ilearn Smart World
- Ngữ pháp Tiếng Anh 6 i-learn Smart World
- Trọn bộ Từ vựng Tiếng Anh 6 ilearn Smart World đầy đủ nhất
- Giải sbt Tiếng Anh 6 - iLearn Smart World
- Bài tập Tiếng Anh 6 iLearn Smart World theo Unit có đáp án
