Nội dung bài viết

    Xem thêm

    Giải SBT Toán 10 trang 48 Tập 1 Cánh diều

    Với Giải SBT Toán 10 trang 48 Tập 1 trong Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 48.

    1 833 23/09/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 trang 48 Tập 1 Cánh diều

    Bài 16 trang 48 SBT Toán 10 Tập 1: Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:

    a) y = 4x2 + 6x – 5;

    b) y = – 3x2 + 10x – 4.

    Lời giải

    a) Hàm số y = 4x2 + 6x – 5, có a = 4 > 0 và ∆ = 62 – 4.4.(– 5) =  116

    Ta có −b2a=−62.4=−34 và −Δ4a=−1164.4=−294

    Khi đó, ta có bảng biến thiên:

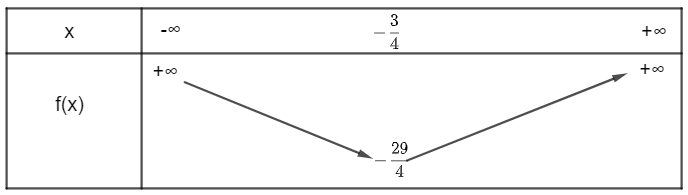
    Sách bài tập Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - Cánh diều (ảnh 1)

    Vậy hàm số nghịch biến trên −∞;−34, hàm số đồng biến trên −34;+∞.

    b) Hàm số y = – 3x2 + 10x – 4, có a = – 3 < 0 và ∆ = 102 – 4.(– 3).(– 4) = 52

    Ta có −b2a=−102.(−3)=53 và −Δ4a=−524.(−3)=133

    Khi đó, ta có bảng biến thiên:

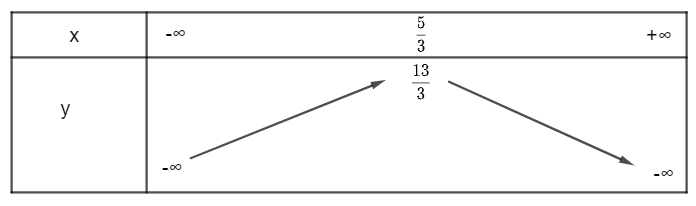
    Sách bài tập Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - Cánh diều (ảnh 1)

    Vậy hàm số đồng biến trên −∞;53, hàm số nghịch biến trên 53;+∞.

    Bài 17 trang 48 SBT Toán 10 Tập 1: Xác định hàm số bậc hai biết hệ số tự do c = 2 và bảng biến thiên tương ứng trong mỗi trường hợp sau:

    a)

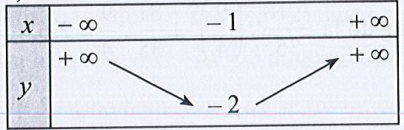
    Sách bài tập Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - Cánh diều (ảnh 1)

    b)

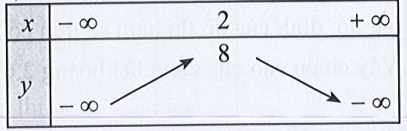
    Sách bài tập Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - Cánh diều (ảnh 1)

    Lời giải

    a) Dựa vào bảng biến thiên ta có:

    −b2a=−1 ⇔ b = 2a

    −Δ4a=−2 ⇔ ∆ = 8a ⇔ b2 – 4ac = 8a

    ⇔ (2a)2 – 4a.2 = 8a

    ⇔ 4a2 – 8a = 8a

    ⇔ 4a2 – 16a = 0

    ⇔ 4a(a – 4) = 0

    ⇔ a = 0 (không thỏa mãn) hoặc a = 4 (thỏa mãn)

    ⇒ b = 2a = 2.4 = 8.

    Vậy hàm số bậc hai cần tìm là y = 4x2 + 8x + 2.

    b) Dựa vào bảng biến thiên ta có:

    −b2a=2 ⇔ b = – 4a

    −Δ4a=8 ⇔ ∆ = – 32a ⇔ b2 – 4ac = – 32a

    ⇔ (4a)2 – 4a.2 = – 32a  

    ⇔ 4a2 – 8a = – 32a

    ⇔ 16a2 + 24a = 0

    ⇔ 8a(2a + 3) = 0

    ⇔ a = 0 (không thỏa mãn) hoặc a = -32 (thỏa mãn)

    ⇒ b = – 4a = – 4.-32 = 6.

    Vậy hàm số bậc hai cần tìm là y = −32x2 + 6x + 2.

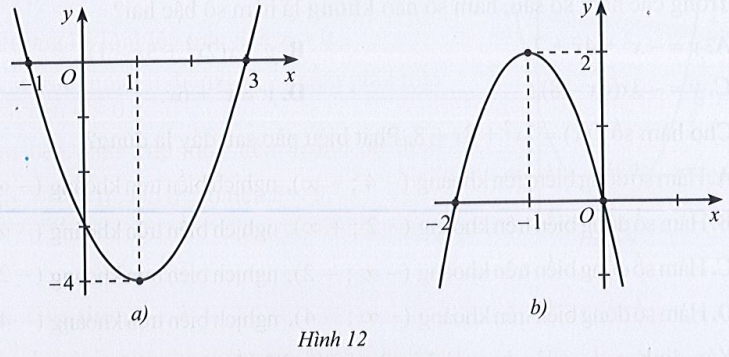
    Bài 18 trang 48 SBT Toán 10 Tập 1: Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi Hình 12a, 12b:

    Sách bài tập Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - Cánh diều (ảnh 1)

    Lời giải

    +) Hình 12a):

    Dựa vào hình vẽ, ta thấy:

    - Đồ thị hàm số cắt trục tung tại điểm có tung độ – 3 nên c = – 3.

    - Điểm đỉnh của parabol có tọa độ (1; – 4) nên ta có:

    −b2a=1 ⇔ b = – 2a

    −Δ4a=−4⇔ ∆ = 16a

    ⇔ b2 – 4ac = 16a

    ⇔ (– 2a)2 – 4a(– 3) = 16a

    ⇔ 4a2 + 12a = 16a

    ⇔ 4a2 – 4a = 0

    ⇔ 4a(a – 1) = 0

    ⇔ a = 0 (không thỏa mãn) hoặc a = 1 (thỏa mãn)

    ⇒ b = – 2a = – 2.1 = – 2.

    Vậy hàm số bậc hai cần tìm là y = x2 – 2x – 3.

    +) Hình 12b):

    Dựa vào hình vẽ, ta thấy:

    - Đồ thị hàm số cắt trục tung tại điểm có tung độ 0 nên c = 0.

    - Điểm đỉnh của parabol có tọa độ (– 1; 2) nên ta có:

    −b2a=−1 ⇔ b = 2a

    −Δ4a=2⇔ ∆ = – 8a

    ⇔ b2 – 4ac = – 8a

    ⇔ (2a)2 – 4a.0 = – 8a

    ⇔ 4a2 = – 8a

    ⇔ 4a2 + 8a = 0

    ⇔ 4a(a + 2) = 0

    ⇔ a = 0 (không thỏa mãn) hoặc a = – 2 (thỏa mãn)

    ⇒ b = 2a = 2.(– 2) = – 4.

    Vậy hàm số bậc hai cần tìm là y = – 2x2 – 4x.

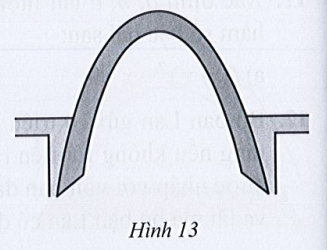
    Bài 19 trang 48 SBT Toán 10 Tập 1: Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao cho khoảng cách giữa hai chân cổng BC là 9 m. Từ một điểm M trên thân cổng người ta đo được khoảng cách tới mặt đất là MK = 1,6 m và khoảng cách từ K tới chân cổng gần nhất là BK = 0,5 m. Tính chiều cao của cổng theo đơn vị mét (làm tròn kết quả đến hàng phần mười).

    Sách bài tập Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - Cánh diều (ảnh 1)

    Lời giải

    Đặt hệ trục tọa độ như hình vẽ:

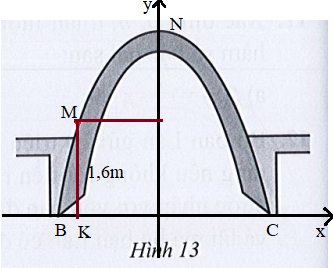
    Sách bài tập Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - Cánh diều (ảnh 1)

    Tọa độ các điểm lần lượt là: B(– 4,5; 0); C(4,5; 0);

    Vì BK = 0,5 m nên OK = 4,5 – 0,5 = 4 m. Do đó M(4; 1,6).

    Cổng có hình parabol nên gọi phương trình hàm số là y = ax2 + bx + c (a ≠ 0) (1).

    Điểm B thuộc parabol nên thay tọa độ điểm B vào (1) ta được:

    0 = a(– 4,5)2 + b(– 4,5) + c ⇔ 20,25a – 4,5b + c = 0 (2).

    Điểm C thuộc parabol nên thay tọa độ điểm C vào (1) ta được:

    0 = a(4,5)2 + b(4,5) + c ⇔ 20,25a + 4,5b + c = 0 (3).

    Điểm M thuộc parabol nên thay tọa độ điểm M vào (1) ta được:

    1,6 = a.42 + b.4 + c ⇔ 16a + 4b + c = 1,6 (4).

    Từ (2), (3) và (4) ta có hệ phương trình: 20,25a−4,5b+c=020,25a+4,5b+c=016a+4b+c=1,6⇔a=−3285b=0c=64885.

    Suy ra parabol cần tìm là: y = −3285x2 + 64885.

    Điểm N là điểm đỉnh của parabol thuộc vào trục tung Oy nên hoành độ điểm N bằng 0.

    Thay x = 0 vào hàm số y = −3285x2 + 64885, ta được y = −3285.02 + 64885 = 64885.

    ⇒ N0;64885.

    Tung độ điểm N cũng chính là chiều cao của cổng và bằng 64885≈7,6 m.

    Vậy chiều cao của cổng khoảng 7,6 m.

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Giải SBT Toán 10 trang 47 Tập 1

    Xem thêm các bài giải sách giáo khoa Toán 10 bộ sách Cánh diều hay, chi tiết khác:

    Bài 9 trang 47 SBT Toán 10 Tập 1: Trong các hàm số sau, hàm số nào không là hàm số bậc hai?...

    Bài 10 trang 47 SBT Toán 10 Tập 1: Cho hàm số f(x) = 2x2 + 8x + 8. Phát biểu nào sau đây là...

    Bài 11 trang 47 SBT Toán 10 Tập 1: Xác định a, b, c lần lượt là hệ số của x2, hệ số của x và hệ...

    Bài 12 trang 47 SBT Toán 10 Tập 1: Bố bạn Lan gửi 10 triệu đồng vào một ngân hàng với lãi...

    Bài 13 trang 47 SBT Toán 10 Tập 1: Xác định parabol y = ax2 – bx + 1 trong mỗi trường hợp...

    Bài 14 trang 47 SBT Toán 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau:...

    Bài 15 trang 47 SBT Toán 10 Tập 1: Cho hàm số y = ax2 + bx + c có đồ thị ở Hình 11. Xác định...

    Bài 16 trang 48 SBT Toán 10 Tập 1: Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm...

    Bài 17 trang 48 SBT Toán 10 Tập 1: Xác định hàm số bậc hai biết hệ số tự do c = 2 và bảng...

    Bài 18 trang 48 SBT Toán 10 Tập 1: Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi...

    Bài 19 trang 48 SBT Toán 10 Tập 1: Trong một công trình, người ta xây dựng một cổng ra vào...

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Bài ôn tập chương 1

    Bài 1: Bất phương trình bậc nhất hai ẩn

    Bài 2: Hệ bất phương trình bậc nhất hai ẩn

    Bài ôn tập chương 2

    Bài 1: Hàm số và đồ thị

               

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 833 23/09/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: