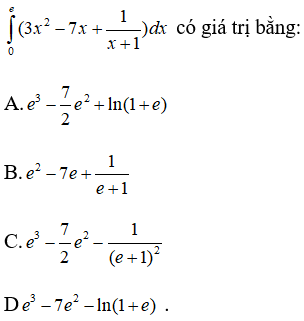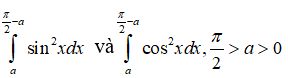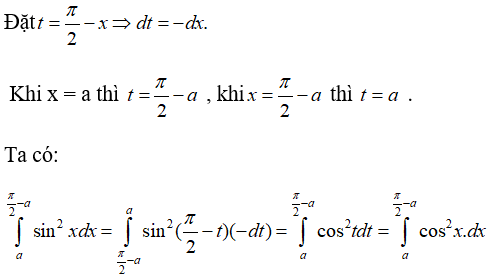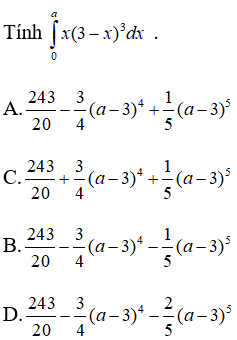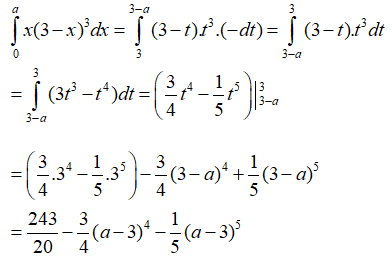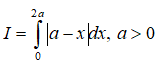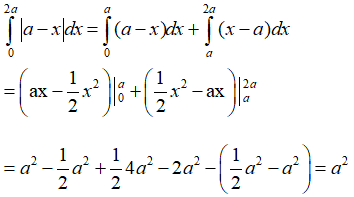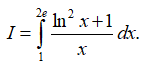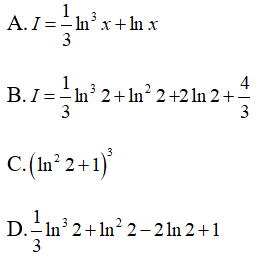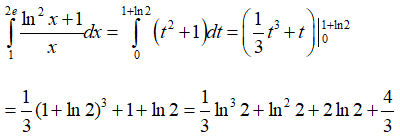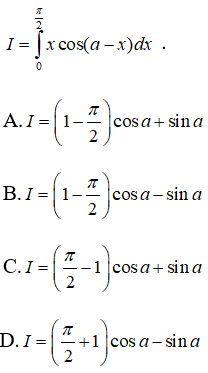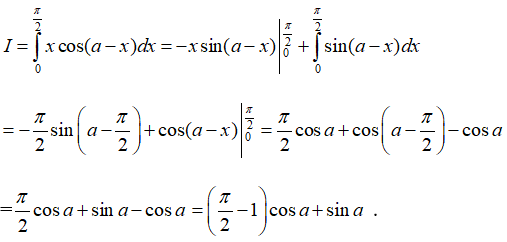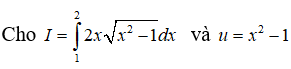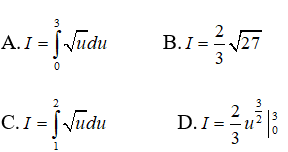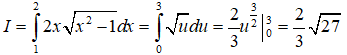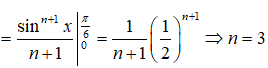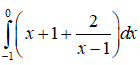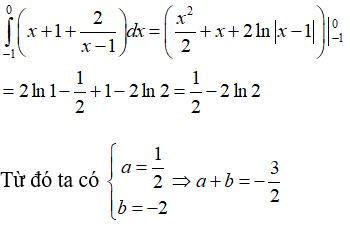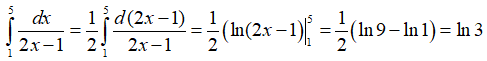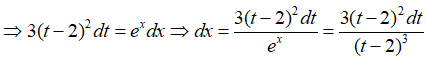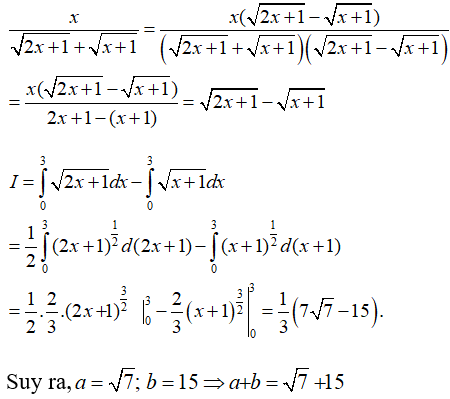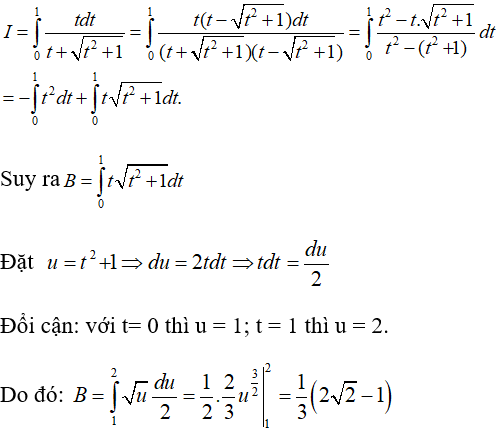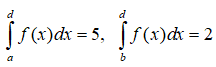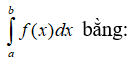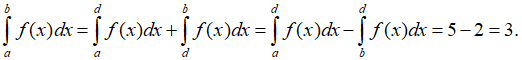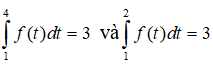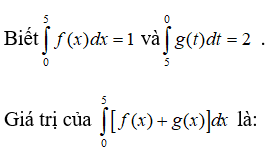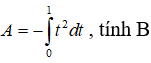Chuyên đề Tích phân (2022) - Toán 12
Với Chuyên đề Tích phân (2022) - Toán 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Tích phân - Toán 12
A. Lý thuyết
I. Khái niệm tích phân
1. Diện tích hình thang cong
- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được gọi là hình thang cong.
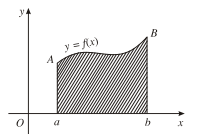
- Ta xét bài toán tìm diện tích hình thang cong bất kì:
Cho hình thang cong giới hạn bởi các đường thẳng x = a; x = b (a < b); trục hoành và đường cong y = f(x), trong đó f(x) là hàm số liên tục, không âm trên đoạn [a; b].
Với mỗi , kí hiệu S(x) là diện tích của phần hình thang cong đó nằm giữa hai đường thẳng vuông góc với Ox lần lượt tại a và b.
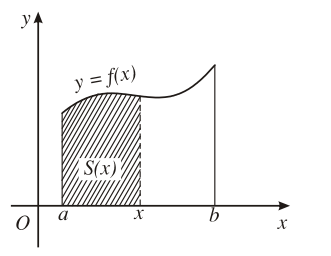
Ta chứng minh được S(x) là một nguyên hàm của f(x) trên đoạn [a; b].
Giả sử F(x) cũng là một nguyên hàm của f(x) thì có một hằng số C sao cho S(x) = F(x) + C.
Vì S(a) = 0 nên F(a) + C = 0 hay C = – F(a).
Vậy S(x) = F(x) – F(a).
Thay x = b vào đẳng thức trên, ta có diện tích của hình thang cần tìm là:
S(b) = F(b) – F(a).
2. Định nghĩa tích phân
Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].
Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b]) của hàm số f(x), kí hiệu
Ta còn dùng kí hiệu để chỉ hiệu số F(b) – F(a).
Vậy
Ta gọi là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.
- Chú ý.
Trong trường hợp a = b hoặc a > b, ta quy ước:
Ví dụ 1.
a)
b)
- Nhận xét.
a) Tích phân của hàm số f từ a đến b có thể kí hiệu là hay . Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào biến x hay t.
b) Ý nghĩa hình học của tích phân.
Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b] thì tích phân là diện tích S của hình thang cong giới hạn bởi đồ thị của f(x), trục Ox và hai đường thẳng x = a; x = b. Vậy .
II. Tính chất của tích phân.
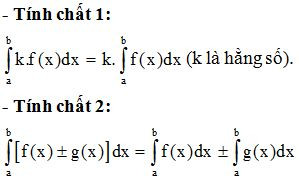
Ví dụ 2. Tính: .
Lời giải:
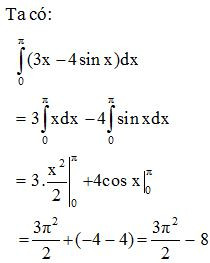
- Tính chất 3.
(a < c < b).
Ví dụ 3. Tính .
Lời giải:
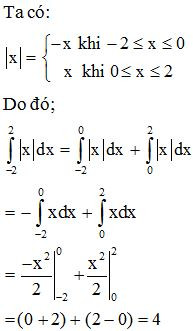
III. Phương pháp tính tích phân
1. Phương pháp đổi biến số
- Định lí:
Cho hàm số f(x) liên tục trên đoạn [a; b]. Giả sử hàm số có đạo hàm liên tục trên đoạn sao cho và .
Khi đó:
Ví dụ 4. Tính .
Lời giải:
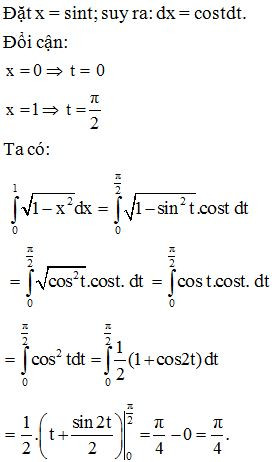
- Chú ý:
Trong nhiều trường hợp ta còn sử dụng phép đổi biến số ở dạng sau:
Cho hàm số f(x) liên tục trên đoạn [a; b]. Để tính , đôi khi ta chọn hàm số u = u(x) làm biến số mới, trong đó trên đoạn [a; b], u(x) có đạo hàm liên tục và .
Giả sử có thể viết: f(x) = g(u(x)). u’(x) với với g(u) liên tục trên đoạn
Khi đó, ta có:
Ví dụ 5. Tính
Lời giải:
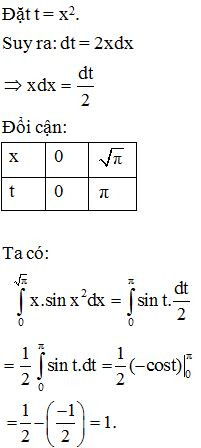
2. Phương pháp tính tích phân từng phần
- Định lí.
Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:
Hay
Ví dụ 6. Tính
Lời giải:
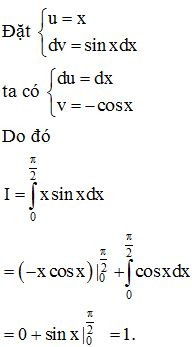
Ví dụ 7. Tính .
Lời giải:
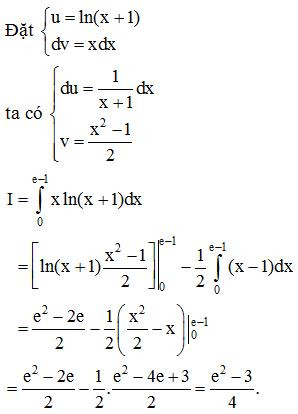
B. Bài tập
I. Bài tập trắc nghiệm
Câu 1: Tích phân
Lời giải:
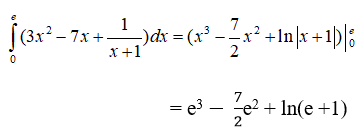
Ta chọn đáp án A
Câu 2: Cho hai tích phân:
Trong các khẳng định sau , khẳng định nào đúng?
Lời giải:
Đặt t = π/2 - x ⇒ dt = -dx Khi x = a thì t = π/2 - a , khi x = π/2 - a thì t = a
Ta có:
Vậy chọn đáp án B.
Câu 3:
Lời giải:
Đặt: t = 3 - x ⇒ dt = - dx .
Khi x = 0 thì t = 3, khi x = a thì t = 3-a.
Vậy chọn đáp án B.
Câu 4: Tính tích phân
A. I = 0
B. I = a2
C. I = -a2
D. I = 2a2 .
Lời giải:
Ta có:
Vậy chọn đáp án B.
Câu 5: Tính tích phân 
Lời giải:
Đặt t = lnx ⇒ dt = (1/x)dx . Khi x = 1 thì t = 0, khi x = 2e thì t = 1+ln2. Ta có:
Vậy chọn đáp án D.
Câu 6: Tính tích phân
Lời giải:
Đặt u = x và dv = cos(a - x)dx ,suy ra du = dx và v = -sin(a-x). Do đó
Vậy chọn đáp án C.
Câu 7:
Khẳng định nào dưới đây là sai?
Lời giải:
Đặt u = x2 - 1 , ta có du = 2xdx. Khi x = 1 thì u = 0, x = 2 thì u = 3. Do đó
Vậy chọn đáp án C.
Câu 8:
Tìm n?
A.6
B.5
C.4
D.3
Lời giải:
Ta có:
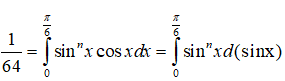
Vậy chọn đáp án D.
Câu 9: Kết quả của tích phân
được viết dưới dạng a+bln2. Tính giá trị của a+b.
Lời giải:
Ta có:
Vậy chọn đáp án D
Câu 10: Giả sử
Giá trị của K là:
A.9
B.3
C.81
D.8
Lời giải:
Ta có:
Do đó, K = 3
II. Bài tập tự luận có lời giải
Câu 1: Cho:
Tính giá trị của a-b.
Lời giải:
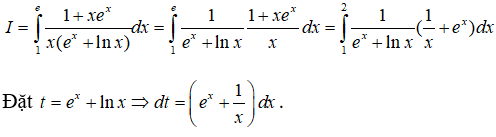
Khi x = 1 thì t = e, khi x = e thì t = ee + 1 .
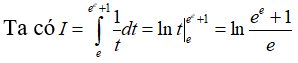
Từ đó suy ra: a = 1; b = 1 nên a – b = 0.
Câu 2: Cho
Giả sử đặt t = + 2 thì ta được:
Lời giải:
⇒(t - 2)3 = ex
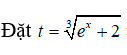
Đổi cận: x = 0 thì t = 3 ; x = 3ln2 thì t = 4
Khi đó
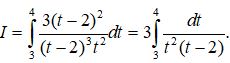
Câu 3: Cho
Khi đó a+b bằng
Lời giải:
Ta có
Câu 4: Cho
Đặt t = x2 . Biết
Lời giải:
Đặt t = x2 ⇒ dt = 2xdx. Ta có:
Câu 5: Nếu
với a < d < b thì
Lời giải:
Ta có:
Câu 6: Cho tích phân
Nếu biến đổi số t = sin2x thì:
Lời giải:
Ta có
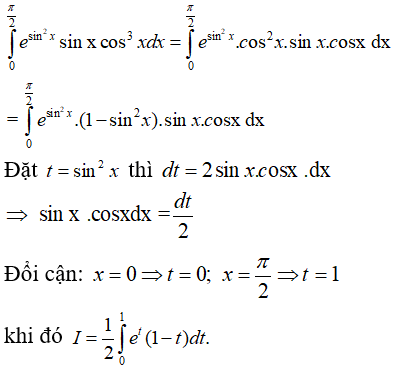
Câu 7: Tính
Lời giải:
Ta có
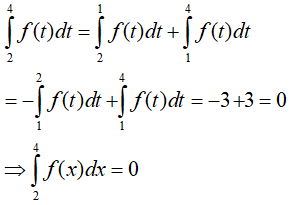
Câu 8:
Lời giải:
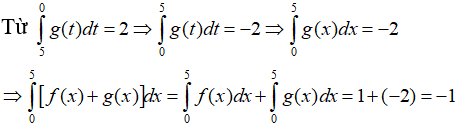
Bài 9:
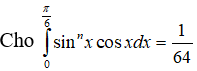
Tìm n?
Lời giải:
Ta có:
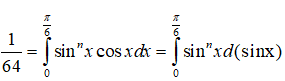
Bài 10: Kết quả của tích phân
được viết dưới dạng a+bln2. Tính giá trị của a+b.
Lời giải:
Ta có:
III. Bài tập vận dụng
Bài 1 Giả sử 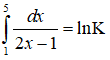Giá trị của K là?
Bài 2 Cho: 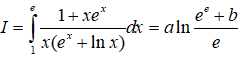Tính giá trị của a-b.
Bài 3 Cho 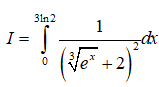Giả sử đặt t = ∛ex + 2 thì ta được?
Bài 4 Cho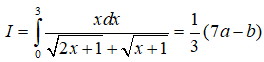. Khi đó a+b bằng?
Bài 5 Cho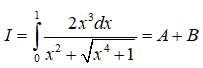 Đặt t = x2 . Biết 
Bài 6 Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = (x -1)e2x ,trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox
Bài 7 Cho tích phân 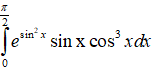. Nếu biến đổi số t = sin2x thì:
Bài 8 Tính tích phân
Bài 9 Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox.
Bài 10 Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x3 - x và đồ thị hàm số y = x - x2.
Xem thêm các bài Chuyên đề Toán lớp 12 hay, chi tiết khác:
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12