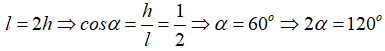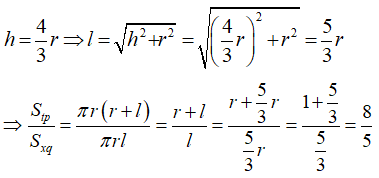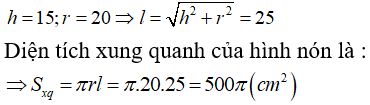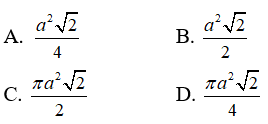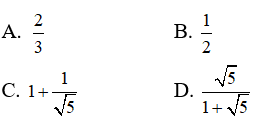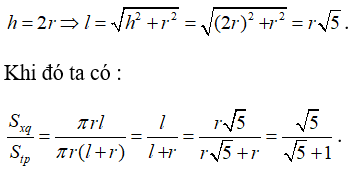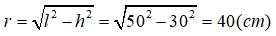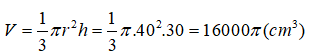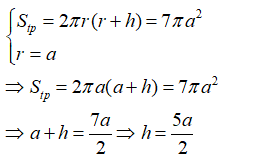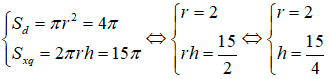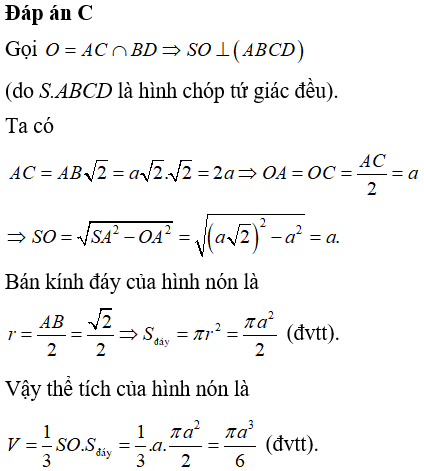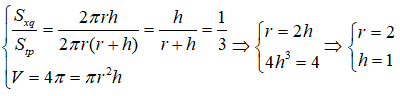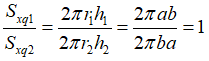Chuyên đề Khái niệm về mặt tròn xoay (2022) - Toán 12
Với Chuyên đề Khái niệm về mặt tròn xoay (2022) - Toán 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Khái niệm về mặt tròn xoay - Toán 12
A. Lý thuyết
I. Sự tạo thành mặt tròn xoay.
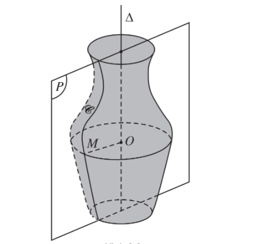
Trong không gian cho mặt phẳng (P) chứa đường thẳng ∆ và một đường C. Khi quay mặt phẳng (P) quanh ∆ một góc 3600 thì mỗi điểm M trên đường C vạch ra một đường tròn có tâm O thuộc ∆ và nằm trên mặt phẳng vuông góc với ∆.
Như vậy, khi quay mặt phẳng (P) quanh đường thẳng ∆ thì đường C sẽ tạo thành một hình được gọi là mặt tròn xoay.
Đường C được gọi là đường sinh của mặt tròn xoay đó. Đường thẳng ∆ được gọi là trục của mặt tròn xoay đó.
II. Mặt nón tròn xoay
1. Định nghĩa.
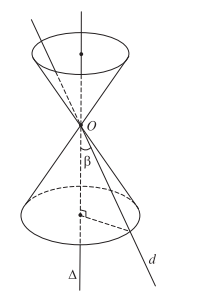
Trong mặt phẳng (P) cho hai đường thẳng d và ∆ cắt nhau tại điểm O và tạo thành góc β với 00 < β < 900. Khi quay mặt phẳng (P) xung quanh ∆ thì đường thẳng d sinh ra một mặt tròn xoay được gọi là mặt nón tròn xoay đỉnh O.
Người thường gọi tắt mặt nón tròn xoay là mặt nón.
Đường thẳng ∆ là trục, đường thẳng d là đường sinh và góc 2β gọi là góc ở đỉnh của mặt nón đó.
2. Hình nón tròn xoay và khối nón tròn xoay.
a) Cho tam giác OIM vuông tại I. Khi quay tam giác đó xung quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.
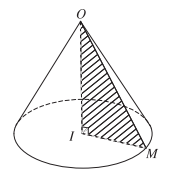
Hình tròn tâm I sinh bởi các điểm thuộc cạnh IM khi quay quanh trục OI được gọi là mặt đáy của hình nón, điểm O được gọi là đỉnh của hình nón.
Độ dài đoạn OI gọi là chiều cao của hình nón, đó cũng chính là khoảng cách từ O đến mặt phẳng đáy. Độ dài đoạn OM gọi là độ dài đường sinh của hình nón.
Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh OM khi quay quanh OI được gọi là mặt xung quanh của hình nón đó.
b) Khối nón tròn xoay là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó. Người ra gọi tắt khối nón tròn xoay là khối nón.
Những điểm không thuộc khối nón được gọi là những điểm ngoài của khối nón. Những điểm thuộc khối nón nhưng không thuộc hình nón ứng với khối nón ấy được gọi là những điểm trong của khối nón.
Ta gọi đỉnh, mặt đáy, đường sinh của một hình nón theo thứ tự là đỉnh, mặt đáy, đường sinh của khối nón tương ứng.
3. Diện tích xung quanh của hình nón tròn xoay.
a) Một hình chóp được gọi là nội tiếp một hình nón nếu đáy của hình chóp là đa giác nội tiếp đường tròn đáy của hình nón và đỉnh của hình chóp là đỉnh của hình nón. Khi đó, ta còn nói hình nón ngoại tiếp hình chóp.
- Định nghĩa: Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính diện tích xung quanh của hình nón.
- Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh.
Sxq = πrl (r là bán kính đường tròn đáy, l là độ dài đường sinh).
- Người ta gọi tổng của diện tích xung quanh và diện tích đáy là diện tích toàn phần của hình nón.
- Chú ý: Diện tích xung quanh, diện tích toàn phần của hình nón tròn xoay cũng là diện tích xung quanh , diện tích toàn phần của khối nón được giới hạn bởi hình nón đó.
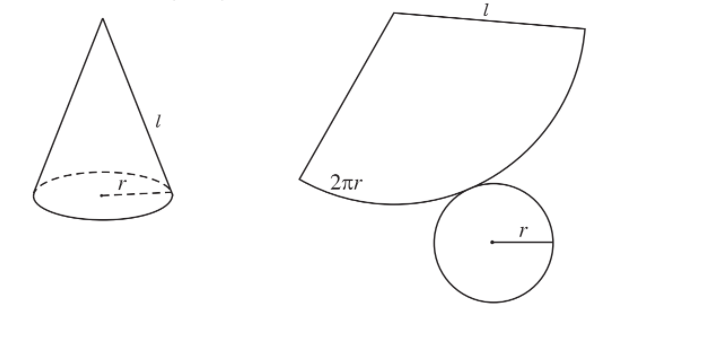
- Nếu cắt mặt xung quanh của hình nón tròn xoay theo một đường sinh rồi trải dài ra trên một mặt phẳng thì ta sẽ được một hình quạt có bán kính bằng độ dài đường sinh của hình nón và một cung tròn có độ dài bằng chu vi đường tròn đáy của hình nón. Ta có thể xem diện tích hình quạt này là diện tích xung quanh của hình nón.
Ví dụ 1. Một hình nón tròn xoay có đường cao h = 20, bán kính đáy r = 25.
a) Tính diện tích xung quanh hình nón đã cho.
b) Tính diện tích toàn phần hình nón đã cho.
Lời giải:

4. Thể tích khối nón tròn xoay.
a) Định nghĩa.
Thể tích của khối nón tròn xoay là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính thể tích khối nón tròn xoay.
Gọi V là thể tích của khối nón tròn xoay có diện tích đáy B và chiều cao h, ta có công thức: V=13B.h
Như vậy, nếu bán kính đáy bằng r thì B=πr2, khi đó: V = 13πr2.h
Ví dụ 2. Trong không gian, cho tam giác ABC cân tại A, AB=a√10, BC = 2a. Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH.
Lời giải:
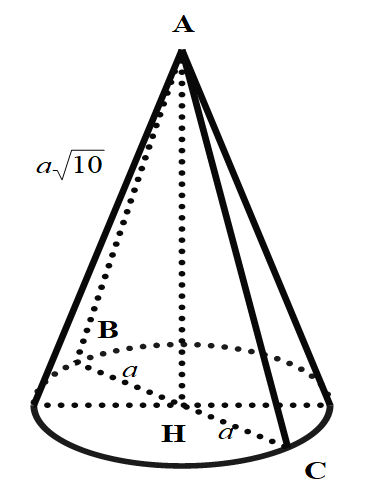

III. Mặt trụ tròn xoay.
1. Định nghĩa
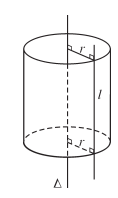
Trong mặt phẳng (P) cho hai đường thẳng ∆ và l song song với nhau, cách nhau một khoảng bằng r. Khi quay mặt phẳng (P) xung quanh ∆ thì đường thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay.
Người ta thường gọi tắt mặt trụ tròn xoay này là mặt trụ. Đường thẳng ∆ gọi là trục, đường thẳng l là đường sinh và r là bán kính của mặt trụ đó.
2. Hình trụ tròn xoay và khối trụ tròn xoay.
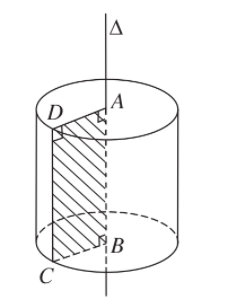
a) Xét hình chữ nhật ABCD. Khi quay hình này xung quanh đường thẳng chứa một cạnh – giả sử là AB; thì đường gấp khúc ADCB tạo thành một hình được gọi là hình trụ tròn xoay hay còn gọi tắt là hình trụ.
- Khi quay quanh AB; hai cạnh AD và BC sẽ vạch ra hai hình tròn bằng nhau gọi là hai đáy của hình trụ, bán kính của chúng gọi là bán kính của hình trụ.
Độ dài đoạn CD gọi là độ dài đường sinh của hình trụ, phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh CD khi quay quanh AB gọi là mặt xung quanh của hình trụ.
Khoảng cách AB giữa hai mặt phẳng song song chứa hai đáy gọi là chiều cao của hình trụ.
b) Khối trụ tròn xoay là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ đó. Khối trụ tròn xoay còn được gọi tắt là khối trụ.
Những điểm không thuộc khối trụ được gọi là những điểm ngoài của khối trụ.
Những điểm thuộc khối trụ nhưng không thuộc hình trụ được gọi là những điểm trong của khối trụ.
Ta gọi mặt đáy, chiều cao, đường sinh, bán kính của một hình trụ theo thú tự là mặt đáy, chiều cao, đường sinh, bán kính của khối trụ tương ứng.
3. Diện tích xung quanh của hình trụ tròn xoay.
a) Một hình lăng trụ gọi là nội tiếp một hình trụ nếu hai đáy của hình lăng trụ nội tiếp hai đường tròn đáy của hình trụ. Khi đó, ta còn nói hình trụ ngoại tiếp hình lăng trụ.
- Định nghĩa: Diện tích xung quanh của hình trụ tròn xoay là giới hạn của diện tích xung quanh của hình lăng trụ đều nội tiếp hình trụ đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính diện tích xung quanh của hình trụ.
- Diện tích xung quanh của hình trụ tròn xoay bằng tích của độ dài đường tròn đáy và độ dài đường sinh:
Sxq = 2πrl ( r là bán kính của hình trụ, l là độ dài đường sinh của hình trụ).
- Chú ý: Diện tích xung quanh, diện tích toàn phần của hình trụ tròn xoay cũng là diện tích xung quanh, diện tích toàn phần của khối trụ được giới hạn bởi hình trụ đó.
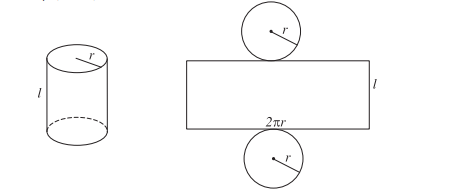
Nếu cắt mặt xung quanh của hình trụ theo một đường sinh, rồi trải ra trên một mặt phẳng thì ta sẽ được một hình chữ nhật có một cạnh bằng đường sinh l và một cạnh bằng chu vi của đường tròn đáy. Độ dài đường sinh l bằng chiều cao h của hình trụ. Khi đó, diện tích hình chữ nhật bằng diện tích xung quanh của hình trụ.
Ví dụ 3. Cho hình vuông ABCD cạnh 8. Gọi M; N lần lượt là trung điểm của AB
và CD. Quay hình vuông ABCD xung quanh MN.
Tính diện tích xung quanh của hình trụ tạo thành
Lời giải:
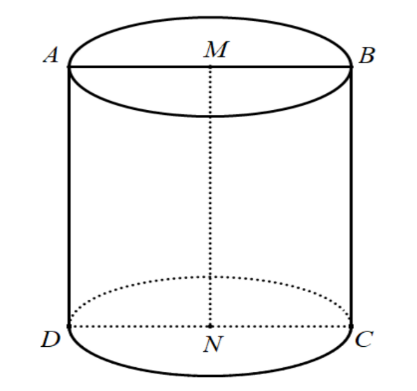
Quay hình vuông ABCD xung quanh MN ta được hình trụ như hình vẽ.
Khi đó, bán kính hình trụ: r=AB2=4;h=AD=8
Diện tích xung quanh của hình trụ tạo thành:
Sxq=2πrh=64π
4. Thể tích khối trụ tròn xoay.
a) Định nghĩa: Thể tích của khối trụ tròn xoay là giới hạn của thể tích khối lăng trụ đều nội tiếp khối trụ đó khi số cạnh đáy tăng lên vô hạn.
b) Công thức tính thể tích khối trụ tròn xoay.
Gọi V là thể tích của khối trụ tròn xoay có diện tích đáy B và chiều cao h, ta có công thức: V = B.h.
Như vậy, nếu bán kính đáy bằng r thì B= πr2, khi đó: V= πr2h.
- Ví dụ 4. Khối trụ có thiết diện qua trục là hình vuông cạnh a = 2 có thể tích là?
Lời giải:
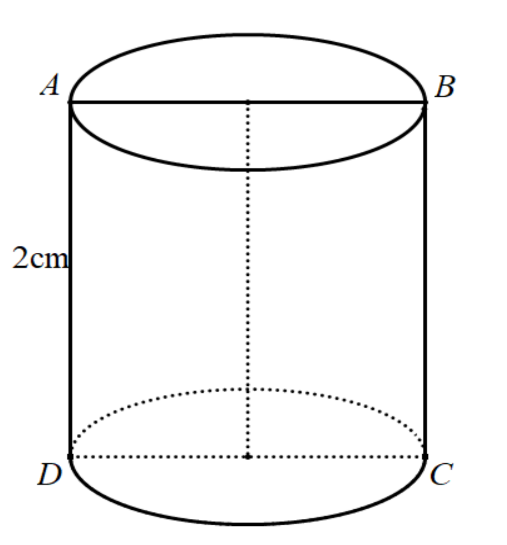
Thiết diện qua trục của khối trụ là hình vuông ABCD như hình vẽ.
Hình vuông cạnh a = 2 nên AB = 2r = 2 .
Suy ra, bán kính của hình trụ là r = 1
Chiều cao hình trụ là h = AD = 2
Thể tích hình trụ: V=πr2h=2π
B. Bài tập
I. Bài tập trắc nghiệm
Câu 1: Hình nón (N) có đường sinh gấp hai lần đường cao. Góc ở đỉnh của hình nón là:
A. 120o
B. 90o
C. 60o
D. 30o
Lời giải:
Gọi 2α là góc ở đỉnh của hình nón. Từ giả thiết ta có:
Câu 2: Hình nón có chiều cao bằng 43 bán kính đáy. Tỉ số giữa diện tích toàn phần và diện tích xung quanh của hình nón là:
A. 43
B. 57
C.85
D. 95
Lời giải:
Từ giả thiết ta có
Câu 3: Hình nón có góc ở đỉnh là 90o và có diện tích xung quanh là π√2 . Độ dài đường cao của hình nón là:
A. 1
B. √2
C. 1√2
D. 2
Lời giải:
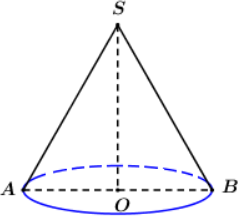
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Câu 4: Cho hình nón tròn xoay có đường cao h=15cm và bán kính đáy r = 20cm. Diện tích xung quanh của hình nón là:
A. 1000π(cm2)
B. 250π(cm2)
C. 375π(cm2)
D. 500π(cm2)
Lời giải:
Từ giả thiết ta có :
Câu 5: Tam giác ABC vuông cân đỉnh A có cạnh huyền là a. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo thành hình nón (N). Diện tích xung quanh của hình nón (N) là:
Lời giải:
Theo cách xây dựng hình nón ta có đường sinh của hình nón là: l = BC = a .
Bán kính đáy của hình nón là: r = AC = BC.sin45o = a√2
Vậy ta có diện tích xung quanh của hình nón (N) là:
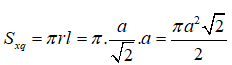
Đáp án đúng là C.
Câu 6: Hình nón (N) có đường sinh gấp hai lần bán kính đáy. Góc ở đỉnh của hình nón là :
A. 120o
B. 60o
C. 30o
D. 0o
Lời giải:
Từ giả thiết ta có l = 2r .
Gọi 2α là góc ở đỉnh của hình nón, khi đó ta có :
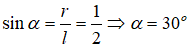
Vậy góc ở đỉnh của hình nón là 60o .
Đáp án đúng là B.
Câu 7: Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón bằng :
Lời giải:
Từ giả thiết ta có:
Đáp án đúng là D.
Câu 8: Một chiếc phễu đựng dầu hình nón có chiều cao là 30cm và đường sinh là 50cm. Giả sử rằng lượng dầu mà chiếc phễu đựng được chính là thể tích của khối nón. Khi đó trong các lượng dầu sau đây, lượng dầu nào lớn nhất chiếc phễu có thể đựng được :
A. 150720π(cm3)
B. 50400π(cm3)
C. 16000π(cm3)
D. 12000π(cm3)
Lời giải:
Từ giả thiết ta có h = 30cm ; l = 50cm. Khi đó ta có
Thể tích khối nón là :
Đáp án đúng là C.
Câu 9: Cho hình trụ có được khi quay hình chữ nhật ABCD quanh trục AB. Biết rằng AB = 2AD = 2a. Thể tích khối trụ đã cho theo a là
A. 2πa3
B.πa3
C. 2πa33
D.πa32
Lời giải:
Từ giả thiết ta có h = AB = 2a, r = AD = a. Khi đó ta có thể tích khối trụ là: V = πr2h = 2πa3 .
Đáp án đúng là A.
Câu 10: Cho hình trụ có diện tích toàn phần là 7πa2 và bán kính đáy là a. Chiều cao của hình trụ là:
A. 3a2
B. 2a
C. 5a3
D. 5a2
Lời giải:
Từ giả thiết ta có:
Đáp án đúng là D.
II. Bài tập tự luận có lời giải
Câu 1: Để làm một thùng phi hình trụ người ta cần hai miếng nhựa hình tròn làm hai đáy có diện tích mỗi hình là 4π(cm2) và một miếng nhựa hình chữ nhật có diện tích là 15π(cm2) để làm thân. Tính chiều cao của thùng phi được làm.
Lời giải:
Diện tích miếng nhựa hình chữ nhật để làm thân bằng diện tích xung quanh của thùng phi.
Từ giả thiết ta có :
Câu 2: Cho hình chữ nhật ABCD có AB = 2AD. Lần lượt quay hình chữ nhật quanh các trục AB, AD ta được hai khối trụ lần lượt gọi là (H1), (H2). Tính tỉ số thể tích của khối trụ (H1) chia cho thể tích của khối trụ (H2)
Câu 3: Cho hình trụ có bán kính đáy bằng a và diện tích toàn phần 6πa2. Diện tích của thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua các trục của hình trụ là :
Lời giải:
Từ giả thiết ta có:
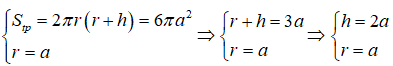
Thiết diện đã cho là một hình chữ nhật có các cạnh lần lượt là h và 2r. Khi đó ta có diện tích thiết diện là : S = 2rh = 4a2 .
Đáp án đúng là C.
Câu 4: Cho khối trụ có diện tích toàn phần là π và có thiết diện cắt bởi mặt phẳng đi qua trục là hình vuông. Thể tích khối trụ là ?
Lời giải:
Từ giả thiết ta có:
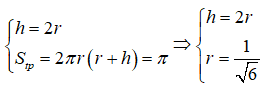
Thể tích khối trụ là :
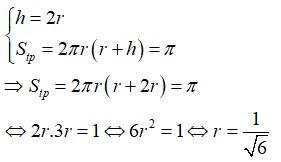
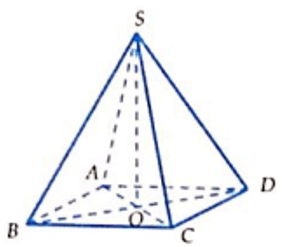
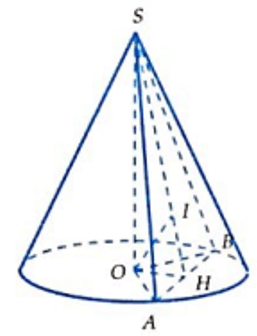
Câu 5: Cho hình chóp tứ giác đều S.ABCD có các cạnh bằng a√2 . Tính thể tích V của khối nón có đỉnh S và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD?
Lời giải:
Câu 6: Cho hình nón S có chiều cao h = a và bán kính đáy r = 2a. Mặt phẳng (P) đi qua S và cắt đường tròn đáy tại A và B sao cho AB = 2√3a Tính khoảng cách d từ tâm của đường tròn đáy đến (P)
Lời giải:
Câu 7: Cho khối nón tròn xoay có bán kính đáy r, đường sinh l và đường cao h. Công thức tính thể tích khối nón là?
Lời giải:
Theo công thức ta có đáp án đúng là C
Câu 8: Hình trụ (H) có diện tích toàn phần là 8π(cm2) và thể tích khối trụ là 3π(cm3) . Tính chiều cao của hình trụ ta được bao nhiêu kết quả?
Lời giải:
Từ giả thiết ta có:
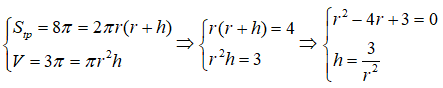
Do r > 0 nên ta có 2 giá trị r thỏa mãn hay có hai hình nón thỏa mãn đề bài
Câu 9: Hình trụ (H) có tỉ số diện tích xung quanh và diện tích toàn phần là 13 . Biết rằng thể tích khối trụ là 4π . Bán kính đáy của hình trụ là:
Lời giải:
Từ giả thiết ta có:
Câu 10: Ta dùng hai hình chữ nhật có cùng kích cỡ để làm thành hai hình trụ (H1) và (H2) bằng cách quay các hình chữ nhật đó, lần lượt theo chiều dài và chiều rộng. Tỉ số hai diện tích xung quanh hình trụ (H1) và hình trụ (H2) là:
Lời giải:
Gọi chiều dài và chiều rộng của hình chữ nhật là a và b.
Hình trụ (H1) có r1 = a ; h1 = b
Hình trụ (H2) có r2 = b ; h2= a
Ta có:
III. Bài tập vận dụng
Bài 1 Cho lăng trụ đứng ABCD.A'B'C'D có đáy ABCD là hình thang, AB = AD = a, CD = 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o . Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được
Bài 2 Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là?
Bài 3 Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h = √3 và góc 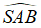
Bài 4 Cho hình trụ có đường cao h và bán kính đáy là r. Trong các khối lăng trụ tứ giác nội tiếp hình trụ thì khối lăng trụ có thể tích lớn nhất bằng?
Bài 5 Một hình nón có đường sinh bằng đường kính đáy. Diện tích xung quanh của hình nón bằng 9π . Tính đường cao h của hình nón.
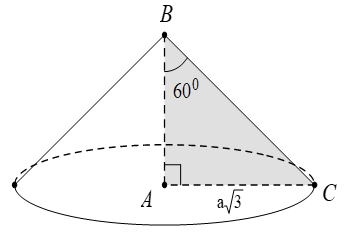
Bài 6 Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 60° . Tính diện tích xung quanh Sxq của hình nón đỉnh S có đáy là hình tròn ngoại tiếp tam giác ABC.
Bài 7 Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy SC = a√6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là?
Bài 8 Cho lăng trụ đứng ABCD.A'B'C'D có đáy ABCD là hình thang, AB = AD = a, CD = 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o . Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được?
Bài 9 Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là?
Bài 10 Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h = √3 và góc 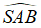
Xem thêm các bài Chuyên đề Toán lớp 12 hay, chi tiết khác:
Chuyên đề Hệ tọa độ trong không gian
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12