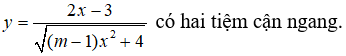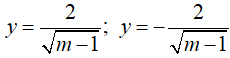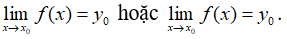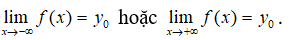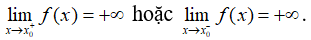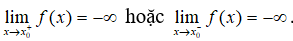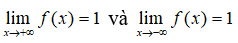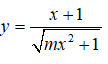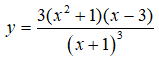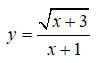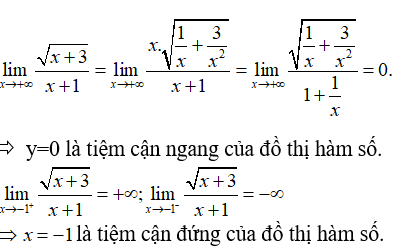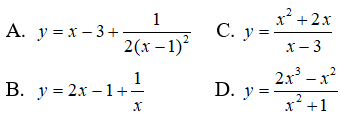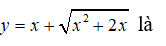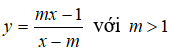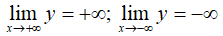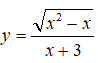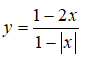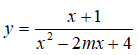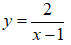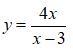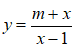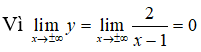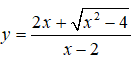Chuyên đề Đường tiệm cận (2022) - Toán 12
Với Chuyên đề Đường tiệm cận (2022) - Toán 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Đường tiệm cận - Toán 12
A. Lý thuyết
I. Đường tiệm cận ngang
- Định nghĩa: Cho hàm số y = f(x) xác định trên một khoảng vô hạn (là khoảng dạng ( a; + ∞); (−∞; b) ; ). Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ví dụ 1. Cho hàm số .
Hàm số xác định trên khoảng .
Đồ thị hàm số có tiệm cận ngang là y = 0 vì
II. Đường tiệm cận đứng
- Định nghĩa:
Đường thẳng x = x0 được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
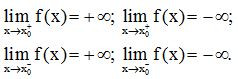
- Ví dụ 2. Tìm đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số .
Lời giải:
Ta có: nên đồ thị hàm số có tiệm cận ngang là y = 1.
Lại có:
Suy ra: đồ thị hàm số có tiệm cận đứng là x = 4.
B. Bài tập
I. Bài tập trắc nghiệm
Bài 1: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
A. m > 0
B. m ≥ 1
C. m > 1
D. Không có giá trị nào của m
Ta có
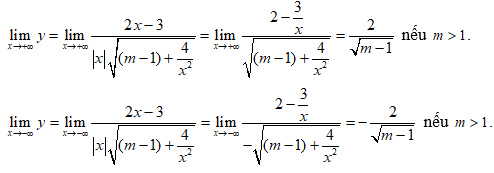
Vậy với m > 1 thì đồ thị hàm số 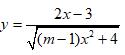
Chọn đáp án C.
Bài 2: Cho các mệnh đề sau
(1) Đường thẳng y = y0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu
(2) Đường thẳng y = y0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu
(3) Đường thẳng x = x0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu
(4) Đường thẳng x = x0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu
Trong các mệnh đề trên, số mệnh đề đúng là:
A.1
B. 2
C. 3
D. 4
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.
Bài 3: Cho hàm số y = f(x) có
Trong các khẳng định dưới đây, khẳng định nào là đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có đúng một tiệm cận ngang.
C. Đồ thị hàm số có hai tiệm cận ngang là y = 1 và y = -1
D. Đồ thị hàm số có hai tiệm cận ngang là x = 1 và x = -1
Từ định nghĩa đồ thị hàm số có đúng một tiệm cận ngang là y=1
Bài 4: Tìm tất cả các giá trị thực của m để đồ thị hàm số
có hai tiệm cận ngang
A.Không tồn tại
B. m < 0
C. m = 0
D. m > 0
Ta có:
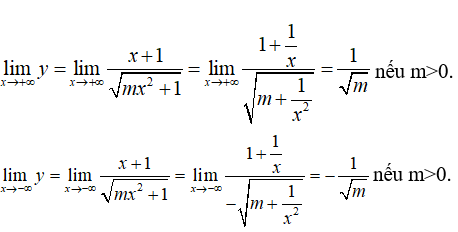
Để hàm số có hai tiệm cận ngang thì m > 0.
Bài 5: Cho hàm số
Trong các khẳng định sau, khẳng định nào đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có đúng một tiệm cận ngang.
C. Đồ thị hàm số có hai tiệm cận ngang là y = 3 và y = -1
D. Đồ thị hàm số có hai tiệm cận ngang là x = 3 và x = -1
Lời giải:
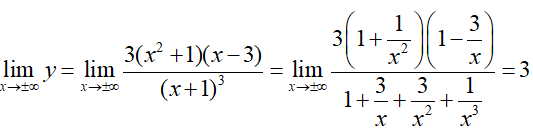
Hàm số có đúng một tiệm cận ngang y=3.
Bài 6: Đồ thị hàm số
có tất cả bao nhiêu tiệm cận?
A. 0
B. 1
C. 2
D. 3
Lời giải:
Vì x ≥ -3 và x ≠ -1, nên ta chỉ xét trường hợp x → +∞
Vậy đồ thị hàm số đã cho có 2 tiệm cận
Bài 7: Hàm số nào sau đây có đồ thị nhận đường thẳng x = 0 làm tiệm cận đứng?
Lời giải:
Ta có:
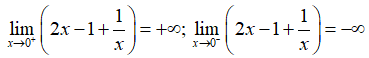
Do đó, đồ thị hàm số 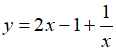
Bài 8: Đường tiệm cận ngang của đồ thị hàm số
A.y = 1
B. y = 0
C. y = -1
D. Không tồn tại
Lời giải:
Ta có:
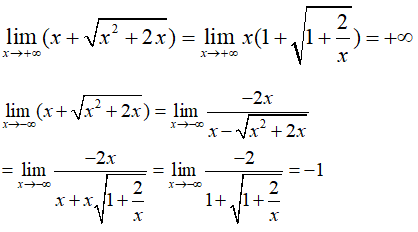
=> y= -1 là tiệm cận ngang của đồ thị hàm số .
Bài 9: Đường tiệm cận đứng của đồ thị hàm số 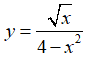
A. x = 0
B. x = 2, x = -2
C. x - 2 = 0
D. x + 2 = 0
Lời giải:
Ta có
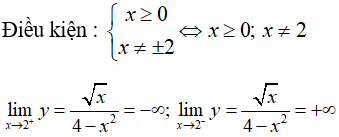
Do đó x - 2 = 0 là tiệm cận đứng của đồ thị hàm số.
Bài 10: Cho hàm số
Hỏi giao điểm của hai đường tiệm cận của đồ thị hàm số trên luôn nằm trên một đường cố định có phương trình nào trong các phương trình sau?
A. y = x
B. x2 + y2 = 1
C. y = x2
D. y = x3
Với m > 1 thì hàm số đã cho không bị suy biến.
y = m là tiệm cận ngang, x = m là tiệm cận đứng của đồ thị hàm số. Vậy giao điểm hai tiệm cận là I(m;m).
Ta có: y1 = x1 nên điểm I thuộc đường thẳng có phương trình y = x.
II. Bài tập tự luận có lời giải
Bài 1. Tìm các đường tiệm cận ngang của các đồ thị hàm số sau:
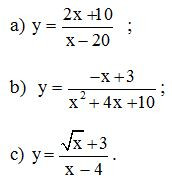
Lời giải:
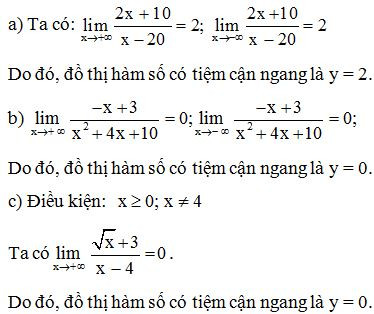
Bài 2. Tìm các đường tiệm cận đứng của các đồ thị hàm số sau:
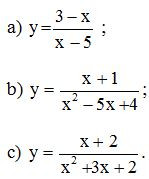
Lời giải:
a) Ta có:
Suy ra: đồ thị hàm số có tiệm cận đứng là x = 5.
b) Ta có: x2 – 5x + 4 = (x – 4)(x – 1)
Khi đó:
Suy ra: đồ thị hàm số có hai tiệm cận đứng là x = 4 và x = 1.
c) Ta có:
Do đó, đồ thị hàm số đã cho có 1 tiệm cận đứng là x = – 1.
Bài 3. Đồ thị hàm số có bao nhiêu tiệm cận?
Lời giải:

Nên đồ thị hàm số có 2 tiệm cận đứng là x = 3 và x = – 2.
Vậy đồ thị hàm số có tất cả 3 tiệm cận (gồm 2 tiệm cận đứng và 1 tiệm cận ngang).
Bài 4 Đồ thị hàm số y = x3 - mx2 + 2 có tất cả bao nhiêu đường tiệm cận?
Lời giải:
Hàm số đã cho xác định với mọi x nên đồ thị hàm số không có TCĐ.
Lại có:
Do đó, đồ thị hàm số không có TCN.
Vậy đồ thị hàm số đã cho không có tiệm cận.
Bài 5: Đồ thị hàm số
có tất cả bao nhiêu đường tiệm cận?
Lời giải:
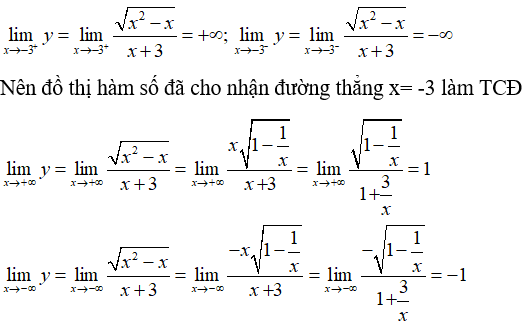
Suy ra, y = 1; y = -1 là hai đường tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.
Bài 6: Đồ thị hàm số
có tất cả bao nhiêu đường tiệm cận?
Lời giải:
Ta có:
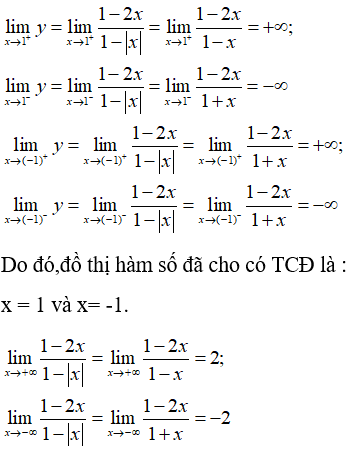
Do đó, đồ thị hàm số có 2 đường tiệm cận ngang là y= 2; y = -2
Vậy đồ thị hàm số đã cho có tất cả 4 đường tiệm cận.
Bài 7: Tìm m để đồ thị hàm số
có ba đường tiệm cận
Lời giải:
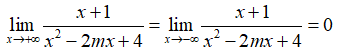
Nên đồ thị hàm số có 1 cận ngang là y= 0
Đồ thị hàm số có ba đường tiệm cận khi đồ thị hàm số có 2 TCĐ
⇒ phương trình x2 - 2mx + 4 = 0 có hai nghiệm phân biệt khác -1.
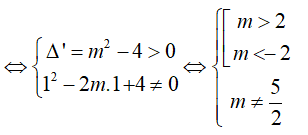
Bài 8: Đồ thị hàm số
có bao nhiêu đường tiệm cận?
Lời giải:
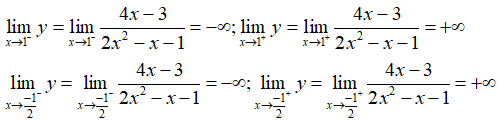
Suy ra x = 1 và là hai tiệm cận đứng của đồ thị hàm số.
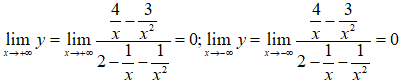
⇒ y = 0 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Bài 9: Tìm mệnh đề sai trong các mệnh đề sau:
A. Đồ thị hàm số
có một tiệm cận đứng và một tiệm cận ngang.
B. Đồ thị hàm số
có một tiệm cận đứng và không có tiệm cận ngang
C. Đồ thị hàm số
có tiệm cận đứng x = 3 và tiệm cận ngang
D. Đồ thị hàm số
có một tiệm cận đứng và một tiệm cận ngang.
Lời giải:
nên đồ thị hàm số có tiệm cận ngang y=0 . Chọn đáp án B.
Bài 10: Cho hàm số
có đồ thị (C). Chọn mệnh đề đúng trong các
mệnh đề sau:
A. Đường y = 2 là một tiệm cận ngang của (C).
B. Đường y = 1 là một tiệm cận ngang của (C).
C. Đường x = - 2 là một tiệm cận đứng của (C).
D. Đường x = 3 là một tiệm cận ngang của (C).
Lời giải:
Ta có
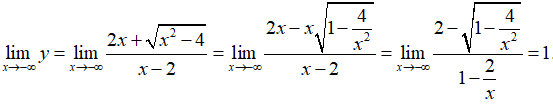
=> y = 1 là một tiệm cận ngang của đồ thị hàm số.
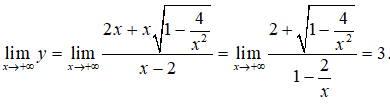
=> y = 3 là một tiệm cận ngang của đồ thị hàm số.
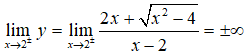
=> x = 2 là tiệm cận đứng của đồ thị hàm số.
III. Bài tập vận dụng
Bài 1 Đồ thị hàm số
có bao nhiêu đường tiệm cận?
Bài 2 Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
Bài 3 Tìm tất cả các giá trị thực của m để đồ thị hàm số
có hai tiệm cận ngang
Bài 4 Đồ thị hàm số
có tất cả bao nhiêu tiệm cận?
Bài 5 Hàm số nào sau đây có đồ thị nhận đường thẳng x = 0 làm tiệm cận đứng?
Bài 6 Đường tiệm cận ngang của đồ thị hàm số
Bài 7 Đường tiệm cận đứng của đồ thị hàm số 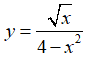
Bài 8 Cho hàm số
Bài 9 Hỏi giao điểm của hai đường tiệm cận của đồ thị hàm số trên luôn nằm trên một đường cố định có phương trình nào trong các phương trình sau?
Bài 10 Đồ thị hàm số y = x3 - mx2 + 2 có tất cả bao nhiêu đường tiệm cận?
Xem thêm các bài Chuyên đề Toán lớp 12 hay, chi tiết khác:
Chuyên đề Sự đồng biến, nghịch biến của hàm số
Chuyên đề Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12