Nội dung bài viết

    Xem thêm

    Biểu diễn miền nghiệm của hệ bất phương trình

    Lời giải Bài 27 trang 32 SBT Toán 10 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

    1 592 05/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 Cánh diều Bài ôn tập chương 2

    Bài 27 trang 32 SBT Toán 10 Tập 1:

    a) Biểu diễn miền nghiệm của hệ bất phương trình 3x−y≤93x+6y≤30x≥00≤y≤4(I).

    b) Tìm x, y là nghiệm của hệ bất phương trình (I) sao cho F = 3x + 4y đạt giá trị lớn nhất.

    Lời giải:

    Vẽ các đường thẳng:

    d1: 3x – y = 9 là đường thẳng đi qua hai điểm có tọa độ là (3; 0) và (0; 9).

    d2: 3x + 6y = 30 là đường thẳng đi qua hai điểm (10; 0) và (0; 5).

    d3: x = 0 là trục tung.

    d4: y = 0 là trục hoành

    d5: y = 4 là đường thẳng đi qua điểm (0; 4) và song song với trục hoành.

    Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ ta được miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình dưới đây chính là miền ngũ giác OABCD với O(0; 0), A(0; 4), B(2; 4), C(4; 3), D(3; 0):

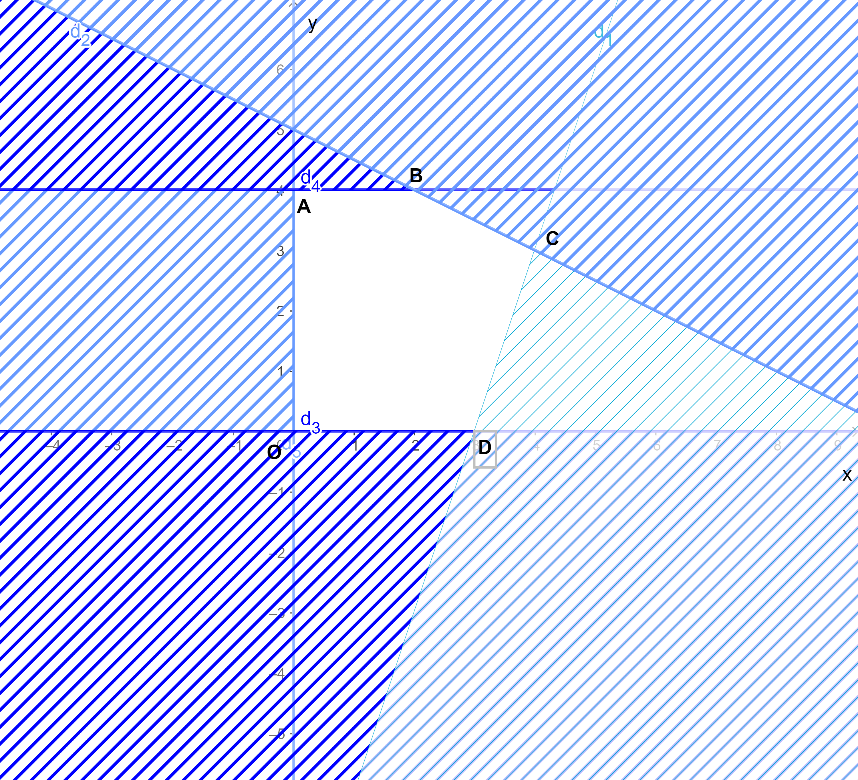
    Sách bài tập Toán 10 Bài ôn tập chương 2 - Cánh diều (ảnh 1)

    b) Biểu thức F = 3x + 4y đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác OABCD.

    Tính giá trị biểu thức F tại các điểm, ta được:

    Tại O(0; 0) với x = 0 và y = 0 thì F = 3.0 + 4.0 = 0;

    Tại A(0; 4) với x = 0 và y = 4 thì F = 3.0 + 4.4 = 16;

    Tại B(2; 4) với x = 2 và y = 4 thì F = 3.2 + 4.4 = 22;

    Tại C(4; 3) với x = 4 và y = 3 thì F = 3.4 + 4.3 = 24;

    Tại D(3; 0) với x = 3 và y = 0 thì F = 3.3 + 4.0 = 9.

    Từ đó giá trị lớn nhất của F là 24 với x = 4 và y = 3.

    Vậy giá trị lớn nhất của F bằng 24 khi x = 4 và y = 3.

    Xem thêm các bài giải sách giáo khoa Toán 10 bộ sách Cánh diều hay, chi tiết khác:

    Bài 20 trang 31 SBT Toán 10 Tập 1: Cặp số nào sau đây không là nghiệm của bất phương trình

    Bài 21 trang 31 SBT Toán 10 Tập 1: Cặp số nào sau đây không là nghiệm của hệ bất phương

    Bài 22 trang 31 SBT Toán 10 Tập 1: Phần không bị gạch (kể cả d) ở Hình 11 là miền nghiệm

    Bài 23 trang 31 SBT Toán 10 Tập 1: Phần không bị gạch (kể cả tia AB, AC) ở Hình 12 là miền

    Bài 24 trang 32 SBT Toán 10 Tập 1: Giá trị nhỏ nhất của biểu thức F = – 2x + y trên miền

    Bài 25 trang 32 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của các bất phương trình sau:

    Bài 26 trang 32 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của các hệ bất phương trình sau:

    Bài 27 trang 32 SBT Toán 10 Tập 1: a) Biểu diễn miền nghiệm của hệ bất phương trình

    Bài 28 trang 32 SBT Toán 10 Tập 1: Một sân bóng đá được tổ chức tại một sân vận động có sức

    Bài 29 trang 32 SBT Toán 10 Tập 1: Một xưởng sản xuất bàn và ghế. Một chiếc bàn cần 1,5 giờ

    Bài 30 trang 33 SBT Toán 10 Tập 1: Hình 13 mô tả sơ đồ một sân khấu gắn với hệ trục tọa độ

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Bài 1: Mệnh đề toán học

    Bài 2: Tập hợp. Các phép toán trên tập hợp

    Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

    Bài 1: Bất phương trình bậc nhất hai ẩn

    Bài 2: Hệ bất phương trình bậc nhất hai ẩn

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 592 05/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: