Nội dung bài viết

    Xem thêm

    Bài 15 trang 106 Toán 11 Tập 2 | Kết nối tri thức Giải Toán lớp 11

    Lời giải Bài 15 trang 106 Toán 11 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 203 07/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 11 Bài tập ôn tập cuối năm

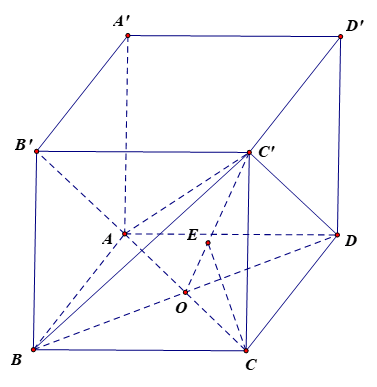
    Bài 15 trang 106 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có AC' = 3 . Khoảng cách giữa hai đường thẳng AB' và BC' bằng

    A. 13 .

    B. 33 .

    C. 32 .

    D. 12 .

    Lời giải:

    Đáp án đúng là: B

    Bài 15 trang 106 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

    Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên O là trung điểm của AC, BD và AC ⊥ BD.

    Có AD // B'C' và AD = B'C' (vì cùng song song và bằng BC) nên ADC'B' là hình bình hành, suy ra AB' // DC'. Do đó AB' // (BDC').

    Khi đó d(AB', BC') = d(AB', (BDC')) = d(A, (BDC')) = d(C, (BDC')) .

    Giả sử hình lập phương ABCD.A'B'C'D' có cạnh là a.

    Xét tam giác ABC vuông tại B có AC=AB2+BC2=a2+a2=a2 .

    Vì CC' ⊥ (ABCD) nên CC' ⊥ AC hay tam giác ACC' vuông tại C.

    Xét tam giác ACC' vuông tại C, có AC'2=AC2+CC'2⇔3=2a2+a2⇒a=1 .

    Do đó hình lập phương ABCD.A'B'C'D' có cạnh là 1 nên AC = 2 .

    Vì O là trung điểm của AC nên CO = 22 .

    Có AC ⊥ BD, BD ⊥ AA' (do AA' ⊥ (ABCD)), suy ra BD ⊥ (ACC'A') mà BD ⊂ (BDC') nên (BDC') ⊥ (ACC'A') .

    Kẻ CE ⊥ C'O tại E.

    Vì (BDC') ⊥ (ACC'A'), (BDC') ∩ (ACC'A') = C'O mà CE ⊥ C'O nên CE ⊥ (BDC').

    Khi đó d(C, (BDC')) = CE.

    Xét tam giác C'CO vuông tại C, CE là đường cao có:

    1CE2=1CC'2+1CO2=11+1222=3⇒CE2=13⇒CE=33.

    Vậy d(AB', BC') =33 .

    Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác: 

    Bài 1 trang 105 Toán 11 Tập 2: Khẳng định nào sau đây là sai? A.cos(α + β) = cosαcosβ + sinαsinβ...

    Bài 2 trang 105 Toán 11 Tập 2: Khẳng định nào sau đây là đúng? A. Hàm số y = sinx tuần hoàn với chu kì π...

    Bài 3 trang 105 Toán 11 Tập 2: Cho dãy số (un) với un = 5n. Số hạng u2n bằng A. 2.5n. B. 25n. C. 10n. D. 5n2...

    Bài 4 trang 105 Toán 11 Tập 2: Dãy số (un) cho bởi công thức số hạng tổng quát nào dưới đây là dãy số tăng? A. un=1n2+1...

    Bài 5 trang 105 Toán 11 Tập 2: Khẳng định nào sau đây là sai? A. Nếu limx→x0fx=L≥0thì limx→x0fx=L...

    Bài 6 trang 105 Toán 11 Tập 2:Hàm số nào dưới đây không liên tục trên ℝ? A. y = tanx. B. y=2x2+3x−1x2+1 ...

    Bài 7 trang 105 Toán 11 Tập 2: Cho 0 < a ≠ 1. Giá trị của biểu thức logaa3⋅a4+a3loga8 bằng A. 194 . B. 9. C. 214 . D. 4712 ...

    Bài 8 trang 105 Toán 11 Tập 2: Cho đồ thị ba hàm số mũ y = ax, y = bx và y = cx như trong hình vẽ dưới đây. Khẳng định nào sau đây là đúng...

    Bài 9 trang 106 Toán 11 Tập 2: Nếu f(x) = sin2x + xe2x thì f"(0) bằng A. 4. B. 5. C. 6. D. 0...

    Bài 10 trang 106 Toán 11 Tập 2: Phương trình tiếp tuyến của đồ thị hàm số y = −2x3 + 6x2 – 5 tại điểm M(3; −5) thuộc đồ thị là A. y = 18x + 49...

    Bài 11 trang 106 Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA ⊥ (ABC), SA = a2. Khoảng cách từ A đến mặt phẳng (SBC) bằng A. 6a11 . B. a6611 ...

    Bài 12 trang 106 Toán 11 Tập 2: Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật. Biết AC = AA' = 2a. Giá trị lớn nhất của thể tích hình hộp ABCD.A'B'C'D' bằng...

    Bài 13 trang 106 Toán 11 Tập 2: Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp B.CMND bằng...

    Bài 14 trang 106 Toán 11 Tập 2: Cho lăng trụ tam giác đều ABC.A'B'C' có AB = 1; AA' = 2. Thể tích khối lăng trụ ABC.A'B'C' bằng...

    Bài 15 trang 106 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có AC' = 3 . Khoảng cách giữa hai đường thẳng AB' và BC' bằng...

    Bài 16 trang 106 Toán 11 Tập 2: Cho mẫu số liệu ghép nhóm về thu nhập của các công nhân tại một doanh nghiệp lớn...

    Bài 17 trang 106 Toán 11 Tập 2: Cho mẫu số liệu ghép nhóm về thu nhập của các công nhân tại một doanh nghiệp lớn...

    Bài 18 trang 106 Toán 11 Tập 2:Vận động viên Tùng thi bắn súng. Biết rằng xác suất để Tùng bắn trúng vòng 10 là 0,2. Mỗi vận động viên được bắn hai lần và hai lần bắn là độc lập...

    Bài 19 trang 107 Toán 11 Tập 2: Hai bạn Sơn và Tùng, mỗi người gieo một con xúc xắc. Xác suất để số chấm xuất hiện trên cả hai con xúc xắc của Sơn và Tùng lớn hơn 1 là...

    Bài 20 trang 107 Toán 11 Tập 2: Hai bạn An và Bình tham gia một trò chơi độc lập với nhau. Xác suất để An và Bình giành giải thưởng tương ứng là 0,8 và 0,6...

    Bài 21 trang 107 Toán 11 Tập 2: Rút gọn các biểu thức sau: a) A=1−2sin2x1+sin2x−1−tanx1+tanx ; b) B=sin4x1+cos4x⋅cos2x1+cos2x−cot3π2−x ;...

    Bài 22 trang 107 Toán 11 Tập 2: Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún cây đu sẽ đưa người chơi dao động qua lại quanh vị trí cân bằng...

    Bài 23 trang 107 Toán 11 Tập 2: Cho cấp số nhân (un) biết rằng ba số u1, u4 và u7 lần lượt là các số hạng thứ nhất, thứ hai và thứ mười của một cấp số cộng có công sai d ≠ 0...

    Bài 24 trang 107 Toán 11 Tập 2: Một công ty đề xuất kí hợp đồng với một người lao động theo một trong hai loại hợp đồng sau...

    Bài 25 trang 108 Toán 11 Tập 2: Tính các giới hạn sau: a) limn→+∞1+3+5+⋯+2n−1n2+2n+3  b) limn→+∞1+23+49+⋯+2n3n ;...

    Bài 26 trang 108 Toán 11 Tập 2: Tìm các giá trị của tham số m để: a) Hàm số f(x) = 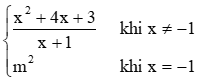Bài 26 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 liên tục tại điểm x = −1;...

    Bài 27 trang 108 Toán 11 Tập 2: Giải các phương trình và bất phương trình sau: a) 31x= 4; b) 2x2−3x= 4; c) log4 (x + 1) + log4 (x – 3) = 3;...

    Bài 28 trang 108 Toán 11 Tập 2: Để xác định tính acid và tính base của các dung dịch, người ta sử dụng khái niệm độ pH. Độ pH của một dung dịch được cho bởi công thức pH = −log[H+],...

    Bài 29 trang 108 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau: a) y=3x2−2x; b) y=1+2x−x2; c) y=tanx2−cotx2;...

    Bài 30 trang 108 Toán 11 Tập 2: Một chất điểm chuyển động có phương trình s(t) = t3 – 3t2 – 9t + 2, ở đó thời gian t > 0 tính bằng giây và quãng đường s tính bằng mét...

    Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác: 

    Bài 32: Các quy tắc tính đạo hàm

    Bài 33: Đạo hàm cấp hai

    Bài tập cuối chương 9 trang 97

    Một vài mô hình toán học sử dụng hàm số mũ và hàm số lôgarit

    Hoạt động thực hành trải nghiệm Hình học

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 203 07/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: