Toán 11 Ôn tập chương 1

Với giải bài tập Toán lớp 11 Ôn tập chương 1 chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11.

1 2,821 14/11/2022

Tải về

Trang trước

Trang sau

Mục lục Giải Toán 11 Ôn tập chương 1

Video giải Toán 11 Ôn tập chương 1

Bài 1 trang 40 SGK Toán lớp 11 Đại số:

a) Hàm số y = cos3x có phải là hàm số chẵn không? Tại sao?

b) Hàm số $y = \tan (x + \frac{π}{5})$ có phải là hàm số lẻ không? Tại sao?

Lời giải:

a) Ta có:

Hàm số y = cos3x có tập xác định $D = ℝ$

$\forall x \in ℝ \Rightarrow - x \in ℝ$ nên D là tập đối xứng

f(-x) = cos3(-x) = cos(-3x) = cos(3x) = f(x)

Vậy hàm số y = cos3x là hàm số chẵn.

b) Điều kiện: $x + \frac{π}{5} \neq \frac{π}{2} + k π \Leftrightarrow x \neq \frac{3 π}{10} + k π$ $(k \in ℤ)$

Ta có:

$y = f (x) = \tan (x + \frac{π}{5})$ có tập xác định là $D = ℝ \ \{\frac{3 π}{10} + k π, k \in ℤ\}$

$\forall x \in D \Rightarrow - x \in D$ nên D là tập đối xứng

$f (- x) = \tan (- x + \frac{π}{5}) = \tan [- (x - \frac{π}{5})] = - \tan (x - \frac{π}{5})$

$- f (x) = - \tan (x + \frac{π}{5})$

Dễ thấy $- \tan (x - \frac{π}{5}) \neq - \tan (x + \frac{π}{5})$ nên $f (- x) \neq - f (x)$ không là hàm số không lẻ.

Bài 2 trang 40 SGK Toán lớp 11 Đại số: Căn cứ vào đồ thị hàm số y = sinx, tìm những giá trị của x trên đoạn $[- \frac{3 π}{2}; 2 π]$ để hàm số đó:

a) Nhận giá trị bằng -1;

b) Nhận giá trị âm.

Lời giải:

Đồ thị y = sinx trên đoạn $[- \frac{3 π}{2}; 2 π]$

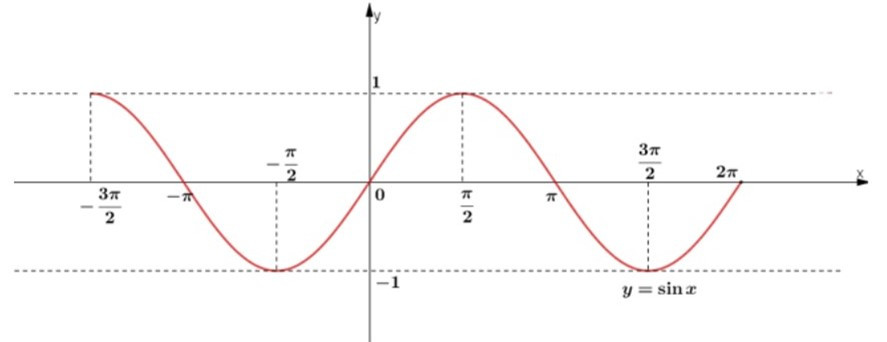
Căn cứ vào đồ thị hàm số y = sinx, tìm những giá trị của x (ảnh 1)

a) Dựa vào đồ thị hàm số y = sinx

Những giá trị của $x \in [- \frac{3 π}{2}; 2 π]$ để hàm y = sinx nhận giá trị bằng -1 là:

$x = \frac{- π}{2}; x = \frac{3 π}{2}$

(Hoành độ giao điểm của đồ thị hàm số và đường thẳng y = -1)

b) Những giá trị của $x \in [- \frac{3 π}{2}; 2 π]$ để hàm y = sinx nhận giá trị âm là:

$x \in (- π; 0) \cup (π; 2 π)$

(Các khoảng mà đồ thị nằm phía dưới trục hoành)

Bài 3 trang 41 SGK Toán lớp 11 Đại số: Tìm giá trị lớn nhất của hàm số sau:

a) $y = \sqrt{2 (1 + \cos x)} + 1$ ;

b) $y = 3 \sin (x - \frac{π}{6}) - 2$ .

Lời giải:

a) $y = \sqrt{2 (1 + \cos x)} + 1$

Ta có:

$- 1 \leq \cos x \leq 1, \forall x \in ℝ$

$\Leftrightarrow 0 \leq 1 + \cos x \leq 2$

$\Leftrightarrow 0 \leq 2 (1 + \cos x) \leq 4$

$\Leftrightarrow 0 \leq \sqrt{2 (1 + \cos x)} \leq 2$

$\Leftrightarrow 1 \leq \sqrt{2 (1 + \cos x)} + 1 \leq 3$

Vậy giá trị lớn nhất của hàm số là 3

Dấu " = " xảy ra khi $\cos x = 1 \Leftrightarrow x = k 2 π (k \in ℤ)$ .

b) $y = 3 \sin (x - \frac{π}{6}) - 2$

Ta có:

$- 1 \leq \sin (x - \frac{π}{6}) \leq 1, \forall x \in ℝ$

$\Leftrightarrow - 3 \leq 3 \sin (x - \frac{π}{6}) \leq 3$

$\Leftrightarrow - 5 \leq 3 \sin (x - \frac{π}{6}) - 2 \leq 1$

$\Leftrightarrow - 5 \leq y \leq 1$

Vậy giá trị lớn nhất của hàm số là 1.

Dấu " = " xảy ra khi $\sin (x - \frac{π}{6}) = 1$

$\Leftrightarrow x - \frac{π}{6} = \frac{π}{2} + k 2 π$

$\Leftrightarrow x = \frac{2 π}{3} + k 2 π, (k \in ℤ)$

Bài 4 trang 41 SGK Toán lớp 11 Đại số: Giải các phương trình sau:

a) $\sin (x + 1) = \frac{2}{3}$ ;

b) $\sin^{2} 2 x = \frac{1}{2}$ ;

c) $\cot^{2} \frac{x}{2} = \frac{1}{3}$ ;

d) $\tan (\frac{π}{12} + 12 x) = - \sqrt{3}$ .

Lời giải:

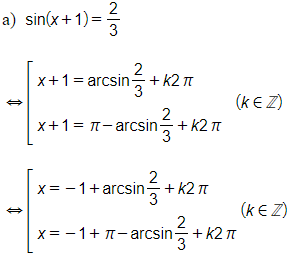
Giải các phương trình sau sin(x+1) = 2/3 (ảnh 1)

Vậy các nghiệm của phương trình là

$x = - 1 + \arcsin \frac{2}{3} + k 2 π$ ; $x = - 1 + π - \arcsin \frac{2}{3} + k 2 π, (k \in ℤ)$

b) $\sin^{2} 2 x = \frac{1}{2}$

$\Leftrightarrow \frac{1 - \cos 4 x}{2} = \frac{1}{2}$

$\Leftrightarrow \cos 4 x = 0$

$\Leftrightarrow 4 x = \frac{π}{2} + k π$ $(k \in ℤ)$

$\Leftrightarrow x = \frac{π}{8} + k \frac{π}{4}, k \in ℤ$

Vậy các nghiệm của phương trình là $x = \frac{π}{8} + k \frac{π}{4}, (k \in ℤ)$ .

c) $\cot^{2} \frac{x}{2} = \frac{1}{3}$

Điều kiện: $\frac{x}{2} \neq k π \Leftrightarrow x \neq k 2 π$ , $k \in ℤ$

Ta có:

$\cot^{2} \frac{x}{2} = \frac{1}{3} \Leftrightarrow [\begin{array}{l} \cot \frac{x}{2} = \frac{\sqrt{3}}{3} (1) \\ \cot \frac{x}{2} = - \frac{\sqrt{3}}{3} (2) \end{array}$

$(1) \Leftrightarrow \cot \frac{x}{2} = \cot \frac{π}{3}$

$\Leftrightarrow \frac{x}{2} = \frac{π}{3} + k π$ , $k \in ℤ$

$\Leftrightarrow x = \frac{2 π}{3} + k 2 π, k \in ℤ$

$(2) \Leftrightarrow \cot \frac{x}{2} = \cot (- \frac{π}{3})$

$\Leftrightarrow \frac{x}{2} = - \frac{π}{3} + k π$ , $k \in ℤ$

$\Leftrightarrow x = - \frac{2 π}{3} + k 2 π, k \in ℤ$

Vậy các nghiệm của phương trình là $x = \pm \frac{2 π}{3} + k 2 π, (k \in ℤ)$ .

d) $\tan (\frac{π}{12} + 12 x) = - \sqrt{3}$

Điều kiện: $\frac{π}{12} + 12 x \neq \frac{π}{2} + k π$

$\Leftrightarrow 12 x \neq \frac{5 π}{12} + k π$

$\Leftrightarrow x \neq \frac{5 π}{144} + \frac{k π}{12}, k \in ℤ$

$\tan (\frac{π}{12} + 12 x) = - \sqrt{3}$

$\Leftrightarrow \tan (\frac{π}{12} + 12 x) = \tan (\frac{- π}{3})$

$\Leftrightarrow \frac{π}{12} + 12 x = \frac{- π}{3} + k π$

$\Leftrightarrow 12 x = \frac{- 5 π}{12} + k π$

$\Leftrightarrow x = \frac{- 5 π}{144} + \frac{k π}{12} (k \in ℤ)$ (t/m)

Vậy các nghiệm của phương trình là: $x = \frac{- 5 π}{144} + \frac{k π}{12} (k \in ℤ)$ .

Bài 5 trang 41 SGK Toán lớp 11 Đại số: Giải các phương trình sau:

a) 2cos²x – 3cosx +1 = 0;

b) 25sin²x + 15sin2x + 9cos²x = 25;

c) 2sinx + cosx = 1;

d) sinx + 1,5cotx = 0.

Lời giải:

a) 2cos²x – 3cosx +1 = 0

Đặt t = cosx với điều kiện $- 1 \leq x < 1$ , khi đó ta có:

2t² – 3t + 1 = 0 $\Leftrightarrow [\begin{array}{l} t = 1 \\ t = \frac{1}{2} \end{array}$

Với t = 1, ta có: cosx = 1 $\Leftrightarrow x = k 2 π, k \in ℤ$

Với $t = \frac{1}{2}$ , ta có:

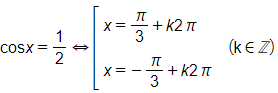
Giải các phương trình sau 2cos2x – 3cosx +1 = 0 (ảnh 1)

Vậy phương trình có các nghiệm là:

$x = k 2 π, x = \pm \frac{π}{3} + k 2 π, k \in ℤ$ .

b) 25sin²x + 15sin2x + 9cos²x = 25

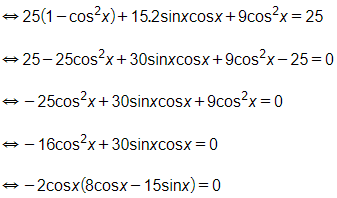
Giải các phương trình sau 2cos2x – 3cosx +1 = 0 (ảnh 1)

$\Leftrightarrow [\begin{array}{l} \cos x = 0 \\ 8 \cos x - 15 \sin x = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} \cos x = 0 \\ 8 \cos x = 15 \sin x \end{array}$

$\Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \frac{8}{15} = \frac{\sin x}{\cos x} \end{array}$

$\Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \tan x = \frac{8}{15} \end{array}$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k π \\ x = \arctan \frac{8}{15} + k π \end{array}, k \in ℤ$

Vậy các nghiệm của phương trình là: $x = \frac{π}{2} + k π, x = \arctan \frac{8}{15} + k π, k \in ℤ$

c) 2sinx + cosx = 1

Chia cả hai vế của phương trình cho $\sqrt{5}$ , ta được:

$\frac{2}{\sqrt{5}} \sin x + \frac{1}{\sqrt{5}} \cos x = \frac{1}{\sqrt{5}}$

Vì ${(\frac{2}{\sqrt{5}})}^{2} + {(\frac{1}{\sqrt{5}})}^{2} = 1$ nên tồn tại một góc $α$ thỏa mãn: $\{\begin{cases} \sin α = \frac{2}{\sqrt{5}} \\ \cos α = \frac{1}{\sqrt{5}} \end{cases}$

Khi đó, phương trình trở thành:

$\sin x \sin α + \cos x \cos α = \cos α$

$\Leftrightarrow \cos (x - α) = \cos α$

$\Leftrightarrow [\begin{array}{l} x - α = α + k 2 π \\ x - α = - α + k 2 π \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 2 α + k 2 π \\ x = k 2 π \end{array} (k \in ℤ)$

Vậy các nghiệm của phương trình là: $x = 2 α + k 2 π; x = k 2 π (k \in ℤ)$ .

d) sinx + 1,5cotx = 0

Điều kiện: $\sin x \neq 0 \Leftrightarrow x \neq k π$

$\sin x + 1, 5 \cot x = 0$

$\Leftrightarrow \sin x + 1, 5 \frac{\cos x}{\sin x} = 0$

$\Rightarrow 2 \sin^{2} x + 3 \cos x = 0$

$\Leftrightarrow 2 (1 - \cos^{2} x) + 3 \cos x = 0$

$\Leftrightarrow 2 \cos^{2} x - 3 \cos x - 2 = 0$

$\Leftrightarrow [\begin{array}{l} \cos x = \frac{- 1}{2} \\ \cos x = 2 (L) \end{array}$

$\Leftrightarrow \cos x = \cos \frac{2 π}{3}$

$\Leftrightarrow [\begin{array}{l} x = \frac{2 π}{3} + k 2 π \\ x = \frac{- 2 π}{3} + k 2 π \end{array} (k \in ℤ)$

Vậy các nghiệm của phương trình là: $x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ$ .

Bài 6 trang 41 SGK Toán lớp 11 Đại số: Phương trình cosx = sinx có số nghiệm thuộc đoạn $[- π; π]$ là:

Lời giải:

Ta có: $\sin x = \cos x \Leftrightarrow \tan x = 1$

$\Leftrightarrow x = \frac{π}{4} + k π (k \in ℤ)$

Vì $x \in [- π, π]$ nên:

$- π \leq \frac{π}{4} + k π \leq π$

$\Leftrightarrow - 1 \leq \frac{1}{4} + k \leq 1$

$\Leftrightarrow - \frac{5}{4} \leq k \leq \frac{3}{4}$

Ta có: $k \in ℤ$ nên $k \in {- 1; 0}$ .

Suy ra phương trình đã cho có hai nghiệm thuộc $[- π, π]$ là $x = - \frac{3 π}{4}; x = \frac{π}{4}$

Chọn đáp án A.

Bài 7 trang 41 SGK Toán lớp 11 Đại số: Phương trình $\frac{\cos 4 x}{\cos 2 x} = \tan 2 x$ có số nghiệm thuộc khoảng $(0; \frac{π}{2})$ là:

Lời giải:

Điều kiện: $\cos 2 x \neq 0 \Leftrightarrow \sin 2 x \neq \pm 1$

Ta có: $\frac{\cos 4 x}{\cos 2 x} = \tan 2 x$

$\Rightarrow \cos 4 x = \tan 2 x . \cos 2 x$

$\Leftrightarrow \cos 4 x = \frac{\sin 2 x}{\cos 2 x} . \cos 2 x$

$\Leftrightarrow 1 - 2 \sin^{2} 2 x = \sin 2 x$

$\Leftrightarrow 2 \sin^{2} 2 x + \sin 2 x - 1 = 0$

$\Leftrightarrow [\begin{array}{l} \sin 2 x = - 1 (L o a i) \\ \sin 2 x = \frac{1}{2} \end{array}$

Ta có: $\sin 2 x = \frac{1}{2} = \sin \frac{π}{6}$

$\Leftrightarrow [\begin{array}{l} 2 x = \frac{π}{6} + k 2 π \\ 2 x = π - \frac{π}{6} + k 2 π \end{array}$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{12} + k π \\ x = \frac{5 π}{12} + k π \end{array} (k \in ℤ)$

Vì $x \in (0; \frac{π}{2})$ nên $x = \frac{π}{12}$ hoặc $x = \frac{5 π}{12}$ .

Vậy có 2 giá trị của $x \in (0; \frac{π}{2})$ thỏa mãn phương trình $\frac{\cos 4 x}{\cos 2 x} = \tan 2 x$ .

Chọn đáp án A.

Bài 8 trang 41 SGK Toán lớp 11 Đại số: Nghiệm dương nhỏ nhất của phương trình sinx + sin2x = cosx + 2cos²x là:

Lời giải:

Ta có:

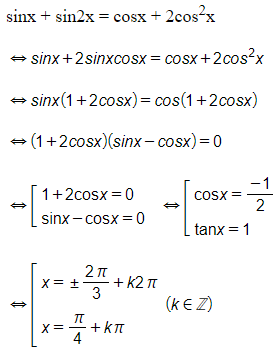
Nghiệm dương nhỏ nhất của phương trình sinx + sin2x = cosx + 2cos2x là (ảnh 1)

Nghiệm dương nhỏ nhất của họ nghiệm: $x = \frac{2 π}{3} + k 2 π$ là $x = \frac{2 π}{3}$

Nghiệm dương nhỏ nhất của họ nghiệm: $x = - \frac{2 π}{3} + k 2 π$ là $x = - \frac{2 π}{3} + 2 π = \frac{4 π}{3}$

Nghiệm dương nhỏ nhất của họ nghiệm: $x = \frac{π}{4} + k π$ là $x = \frac{π}{4}$ .

Suy ra nghiệm dương nhỏ nhất của phương trình đã cho là $x = \frac{π}{4}$ .

Chọn đáp án C.

Bài 9 trang 41 SGK Toán lớp 11 Đại số: Nghiệm âm lớn nhất của phương trình 2tan²x + 5tanx + 3 = 0 là:

Lời giải:

Ta có: 2tan²x + 5tanx + 3 = 0

$\Leftrightarrow [\begin{array}{l} \tan x = - 1 (1) \\ \tan x = - \frac{3}{2} (2) \end{array}$

(1) $\Leftrightarrow t a n x = - 1$

$\Leftrightarrow x = - \frac{π}{4} + k π, k \in ℤ$

(2) $\Leftrightarrow \tan x = - \frac{3}{2}$

$\Leftrightarrow x = \arctan (- \frac{3}{2}) + k π, k \in ℤ$

Nghiệm âm lớn nhất của họ nghiệm $x = - \frac{π}{4} + k π$ là $x = - \frac{π}{4}$ .

Nghiệm âm lớn nhất của họ nghiệm $x = \arctan (- \frac{3}{2}) + k π$ là

$x = \arctan (- \frac{3}{2})$

$Mà \arctan (- \frac{3}{2}) \approx - 0, 983$

$- \frac{π}{4} \approx - 0, 785 \Rightarrow - \frac{π}{4} > \arctan (- \frac{3}{2})$

Vậy nghiệm âm lớn nhất của phương trình là $x = - \frac{π}{4}$ .

Chọn đáp án B.

Bài 10 trang 41 SGK Toán lớp 11 Đại số: Phương trình 2tanx – 2cotx – 3 = 0 có số nghiệm thuộc khoảng $(\frac{- π}{2}; π)$ là:

Lời giải:

Điều kiện: $x \neq k \frac{π}{2}, k \in ℤ$

Ta có: 2tanx – 2cotx – 3 = 0

$\Leftrightarrow 2 \tan x - \frac{2}{\tan x} - 3 = 0$ (vì tanx . cotx = 1)

$\Rightarrow 2 t a n^{2} x - 3 t a n x - 2 = 0$

$\Leftrightarrow [\begin{array}{l} \tan x = 2 \\ \tan x = \frac{- 1}{2} \end{array}$

Dựa vào tương giao của đồ thị hàm số y = tanx và hai đường thẳng y = 2; $y = \frac{- 1}{2}$

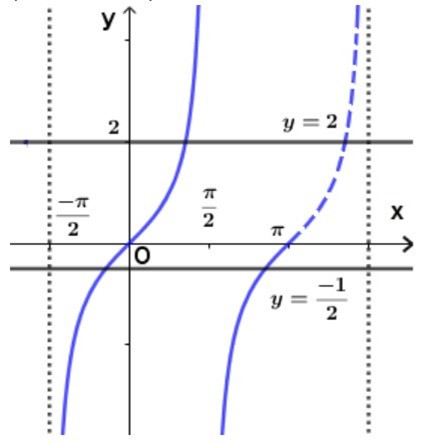
Phương trình 2tanx – 2cotx – 3 = 0 có số nghiệm thuộc khoảng (ảnh 1)

Thấy phương trình có 3 nghiệm thuộc khoảng $(\frac{- π}{2}; π)$

Chọn đáp án C.

Xem thêm lời giải bài tập Toán lớp 11 Đại số và Giải tích hay, chi tiết khác:

Bài 1: Quy tắc đếm

Bài 2: Hoán vị - chỉnh hợp – tổ hợp

Bài 3: Nhị thức Niu-tơn

Bài 4: Phép thử và biến cố

Bài 5: Xác suất của biến cố

Xem thêm tài liệuToán lớp 11 Đại số và Giải tích hay, chi tiết khác:

Lý thuyết Ôn tập chương 1

Trắc nghiệm Ôn tập chương 1 có đáp án

1 2,821 14/11/2022

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3