Nội dung bài viết

    Xem thêm

    Toán 11 Bài 3: Nhị thức Niu-tơn

    Với giải bài tập Toán lớp 11 Bài 3: Nhị thức Niu-tơn chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11.

    1 2,306 29/10/2022
    Tải về
    Trang trước
    Trang sau  

    Mục lục Giải Toán 11 Bài 3: Nhị thức Niu-tơn

    Video giải Toán 11 Bài 3: Nhị thức Niu-tơn

    Hoạt động 1 trang 55 SGK Toán lớp 11 Đại số: Khai triển biểu thức (a + b)4 thành tổng các đơn thức.

    Lời giải :

    (a + b)4 = (a + b)3(a + b)

    = (a3 + 3a2b + 3ab2 + b3)(a + b)

    = a4 + 3a3b + 3a2b2 + ab3 + a3b + 3a2b2 + 3ab3 + b4

    = a4 + 4a3b + 6a2b2 + 4ab3 + b4

    Hoạt động 2 trang 57 SGK Toán lớp 11 Đại số: Dùng tam giác Pa-xcan, chứng tỏ rằng:

    a) 1+2+3+4 =C251+2+3+4 =C25 ;

    b) 1+2+.....+7=C281+2+.....+7=C28;

    Lời giải :

    a) Dựa vào tam giác Pa-xcan: C14=4C14=4; C24=6C24=6

    C25=C14+C26=4+6=10C25=C14+C26=4+6=10

    Mà: 1 + 2 + 3 + 4 = 10

    Suy ra 1+2+3+4 =C251+2+3+4 =C25.

    b) Dựa vào tam giác Pa-xcan: C17=7C17=7; C27=21C27=21

     C28= C17+ C27=7+21=28C28=C17+C27=7+21=28

    Mà: 1 + 2 + … + 7 = 28

    Suy ra  1+2+…+7=C281+2+…+7=C28.

    Bài tập 1 trang 57 SGK Toán lớp 11 Đại số: Viết khai triển theo công thức nhị thức Niu-tơn:

    a) (a + 2b)5

    b)  (a−√2)6(a−√2)6

    c)  (x−1x)13(x−1x)13

    Lời giải:

    a) (a + 2b)5

    Viết khai triển theo công thức nhị thức Niu-tơn (ảnh 1)

    = a5 + 5a4.2b + 10a3.(2b)2 + 10a2.(2b)3 + 5a.(2b)4 + (2b)5

    = a5 +10a4b + 40a3b2 + 80a2b3 + 80ab4 + 32b5

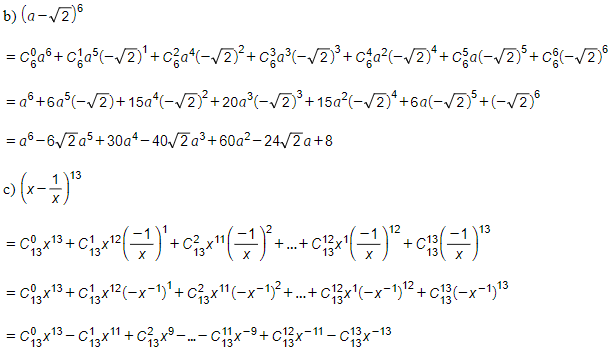
    Viết khai triển theo công thức nhị thức Niu-tơn (ảnh 1)

    Bài tập 2 trang 58 SGK Toán lớp 11 Đại số: Tìm hệ số của x3 trong khai triển của biểu thức:

    (x+2x2)6(x+2x2)6.

    Lời giải:

    Số hạng tổng quát:

    (x+2x2)6=∑6k=1Ck6.x6−k.(2x2)k(x+2x2)6=∑6k=1Ck6.x6−k.(2x2)k

    =∑6k=1Ck6.x6−k.2k(x2)k=∑6k=1Ck6.x6−k.2k(x2)k

    =∑6k=1Ck6.x6−k.2kx2k=∑6k=1Ck6.x6−k.2kx2k

    =∑6k=1Ck6x6−k−2k.2k=∑6k=1Ck6x6−k−2k.2k

    =∑6k=1Ck6.2k.x6−3k=∑6k=1Ck6.2k.x6−3k

    Số hạng chứa x3 ứng với 6 – 3k = 3. Suy ra k = 1

    Vậy hệ số của x3 trong khai triển của biểu thức đã cho là: C16.21=2.6=12C16.21=2.6=12

    Bài tập 3 trang 58 SGK Toán lớp 11 Đại số: Biết hệ số của x2 trong khai triển của (1 – 3x)n là 90. Tìm n.

    Lời giải:

    Số hạng tổng quát

      Tk+1=Ckn.1n−k.(−3x)kTk+1=Ckn.1n−k.(−3x)k=Ckn.(−3)k.xk=Ckn.(−3)k.xk

    Hệ số của số hạng chứa x2 ứng với k = 2 hay hệ số của x2 là C2n.(−3)2=9C2nC2n.(−3)2=9C2n

    Theo bài ra ta có:

    9C2n=90⇔C2n=109C2n=90⇔C2n=10

    ⇔n!2!(n−2)!=10⇔n(n−1)(n−2)!2!(n−2)!=10⇔n(n−1)2=10⇔n(n–1)=20⇔n2–n–20=0⇔[n=5 (TM)n=−4 (Loại)

    Vậy n = 5.

    Bài tập 4 trang 58 SGK Toán lớp 11 Đại số: Tìm số hạng không chứa x trong khai triển của (x3+1x)8.

    Lời giải:

    Số hạng tổng quát trong khai triển của (x3+1x)8 là: Ck8.(x3)8−k.(x−1)k=Ck8.x24−4k

    Số hạng không chứa x trong triển khai của (x3+1x)8 tương đương với: 24 – 4k = 0.

    Suy ra k = 6

    Vậy số hạng không chứa x trong khai triển của (x3+1x)8 là C68=28.

    Bài tập 5 trang 58 SGK Toán lớp 11 Đại số: Từ khai triển của biểu thức (3x – 4)17 thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.

    Lời giải:

    Sử dụng khai triển của nhị thức Newton ta có:

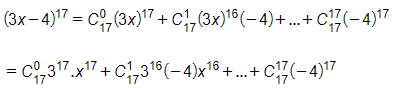
    Từ khai triển của biểu thức (3x – 4)^17 thành đa thức (ảnh 1)

    Ta thấy, tổng các hệ số trong khai triển (3x – 4)17 là:

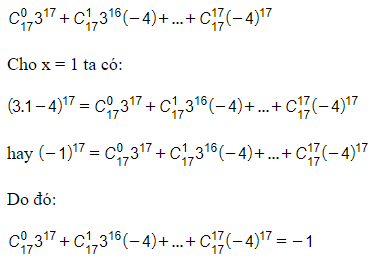
    Từ khai triển của biểu thức (3x – 4)^17 thành đa thức (ảnh 1)

    Vậy tổng các hệ số của đa thức nhận được bằng -1.

    Bài tập 6 trang 58 SGK Toán lớp 11 Đại số: Chứng minh rằng:

    a) 1110 – 1 chia hết cho 100;

    b) 101100 – 1 chia hết cho 10 000;

    c) √10[(1+√10)100−(1−√10)100] là một số nguyên.

    Lời giải:

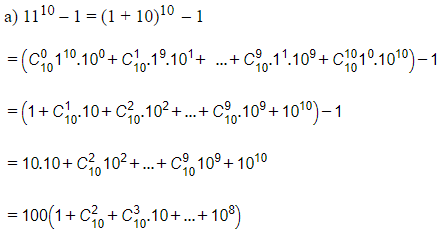
    Chứng minh rằng (11^10) – 1 chia hết cho 100 (ảnh 1)

    Tổng sau cùng là tích của 100 với một tổng nên nó chia hết cho 100 suy ra 1110 – 1  chia hết cho 100 .

    Vậy 1110 – 1 chia hết cho 100.

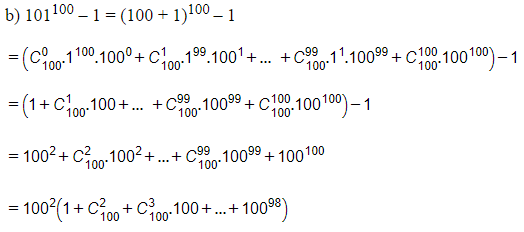
    Chứng minh rằng (11^10) – 1 chia hết cho 100 (ảnh 1)

    Tổng sau cùng chia hết cho 1002  = 10 000 nên 101100 – 1 chia hết cho 10 000.

    c) Ta có:

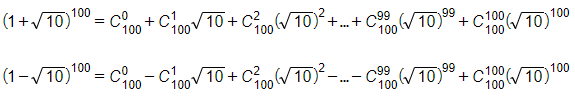
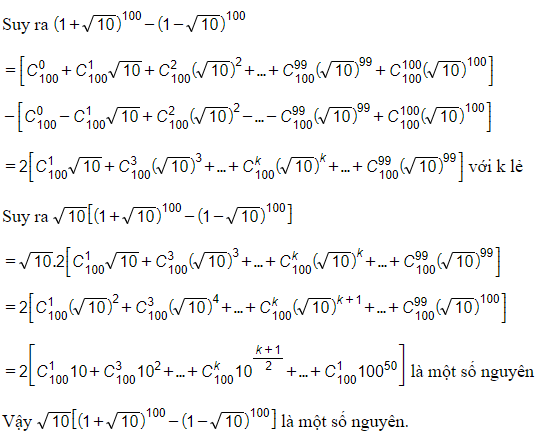
    Chứng minh rằng (11^10) – 1 chia hết cho 100 (ảnh 1)

    Chứng minh rằng (11^10) – 1 chia hết cho 100 (ảnh 1)

    •  
    •  

    Bài giảng Toán 11 Bài 3: Nhị thức Niu-tơn

    Xem thêm lời giải bài tập Toán lớp 11 Đại số và Giải tích hay, chi tiết khác:

    Bài 4: Phép thử và biến cố

    Bài 5: Xác suất của biến cố

    Ôn tập chương 2

    Bài 1: Phương pháp quy nạp toán học

    Bài 2: Dãy số

    Xem thêm tài liệu Toán lớp 11 Đại số và Giải tích hay, chi tiết khác:

    Lý thuyết Nhị thức Niu-tơn

    Trắc nghiệm Nhị Thức Newton có đáp án

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,306 29/10/2022
    Tải về
    Trang trước
    Trang sau  

    Xem thêm các chương trình khác: