Toán 11 Bài 4: Cấp số nhân

Mục lục Giải Toán 11 Bài 4: Cấp số nhân

Video giải Toán 11 Bài 4: Cấp số nhân

Hoạt động 1 trang 98 SGK Toán lớp 11 Đại số: Tục truyền rằng nhà vua Ấn Độ cho phép người phát minh ra bàn cờ Vua được lựa chọn một phần thưởng tùy theo sở thích. Người đó chỉ xin nhà vua thưởng cho số thóc bằng số thóc được đặt lên 64 ô của bàn cờ như sau: Đặt lên ô thứ nhất của bàn cờ một hạt thóc, tiếp ô thứ hai hai hạt, … cứ như vậy, số hạt thóc ở ô sau gấp đôi số hạt thóc ở ô trước cho đến ô cuối cùng.

Hãy cho biết số hạt thóc ở các ô từ ô thứ nhất đến thứ sáu của bàn cờ.

Lời giải:

Số hạt thóc ở các ô từ ô thứ nhất đến thứ sáu là: 1; 2; 4; 8; 16; 32.

Hoạt động 2 trang 99 SGK Toán lớp 11 Đại số: Hãy đọc hoạt động 1 và cho biết ô thứ 11 có bao nhiêu hạt thóc?

Lời giải:

Từ câu hỏi 1 ta thấy:

Ô thứ 1 có 1 = 2⁰ = 2^1–1 hạt thóc.

Ô thứ 2 có 2 = 2¹ = 2²⁻¹ hạt thóc.

Ô thứ 3 có 4 = 2² = 2³⁻¹ hạt thóc.

Ô thứ 4 có 8 = 2³ = 2^{4 – 1} hạt thóc.

Ô thứ 5 có 16 = 2⁴ = 2⁵⁻¹ hạt thóc.

...

Tổng quát: Ô thứ n có 2ⁿ⁻¹ hạt thóc.

Ô thứ 11 có: 2¹¹⁻¹ = 2¹⁰ = 1024 hạt thóc.

Hoạt động 3 trang 101 SGK Toán lớp 11 Đại số: Cho cấp số nhân (u_n) với

u₁ = -2 và $q=-\frac{1}{2}$.

a) Viết năm số hạng đầu của nó.

b) So sánh $u_2^2$ với tích u₁.u₃ và $u_3^2$ với tích u₂.u₄.

Nêu nhận xét tổng quát từ kết quả trên.

Lời giải:

a) Ta có u₁ = -2

$$\begin{gathered} u_2=u_1.q=-2.\frac{-1}{2}=1 \\ {u}_3=u_2.q=1.\frac{-1}{2}=-\frac{1}{2} \\ {u}_4=u_3.q=-\frac{1}{2}.\frac{-1}{2}=\frac{1}{4} \\ {u}_5=u_4.q=\frac{1}{4}.\frac{-1}{2}=-\frac{1}{8} \end{gathered}$$
b) Ta có: $u_2^2=1^2=1$

$$\begin{gathered} u_1.u_3=-2.\frac{-1}{2}=1 \\ \Rightarrow u_2^2=u_1.u_3 \end{gathered}$$

Lại có: $u_3^2={\left(-\frac{1}{2}\right)}^2=\frac{1}{4}$

$$\begin{gathered} u_2.u_4=1.\frac{1}{4}=\frac{1}{4} \\ \Rightarrow u_3^2=u_2.u_4 \end{gathered}$$

Do đó $u_k^2=u_{k-1}.u_{k+1}$; $k\ge 2$.

Hoạt động 4 trang 101 SGK Toán lớp 11 Đại số: Tính tổng số các hạt thóc ở 11 ô đầu của bàn cờ nêu ở hoạt động 1.

Lời giải:

Ta có:

u₁ = 1

u₂ = 2

u₃ = 2²

...

u₁₁ = 2¹⁰

Suy ra S = u₁ + u₂ +...+ u₁₀ = 1 + 2 + 2² +...+ 2¹⁰

Suy ra 2S = 2 + 2² +...+ 2¹⁰ + 2¹¹

Suy ra 2S – S = (2 + 2² +...+ 2¹⁰ + 2¹¹) − (1 + 2 + 2² +...+ 2¹⁰)

Suy ra S = 2¹¹ – 1 = 2047

Cách tổng quát:

Ta có:

S = u₁ + u₂ + u₃ + u₄ + u₅ + u₆ + u₇ + u₈ + u₉ + u₁₀ + u₁₁

= u₁ + u₁.q + u₁.q² +⋯+ u₁.q⁹ + u₁.q¹⁰ (1)

Suy ra S.q = u₁.q + u₁.q² +⋯+ u₁.q⁹ + u₁.q¹⁰ + u₁.q¹¹ (2)

Lấy (1) trừ (2), ta được:

(1− q)S = u₁(1 − q¹¹)

$\Rightarrow S=\frac{u_1\left(1-q^{11}\right)}{1-q}$

Vậy tổng số hạt thóc của 11 ô đầu là 

$S=\frac{1\left(1-2^{11}\right)}{1-2}=2^{11}-1=2047$

Hoạt động 5 trang 102 SGK Toán lớp 11 Đại số: Tính tổng $S=1+\frac{1}{3}+\frac{1}{3^2}+\mathrm{...}+\frac{1}{3^n}$.

Lời giải:

Cách 1:

Cấp số nhân có u₁ = 1, $q=\frac{1}{3}$

S là tổng của (n + 1) số hạng đầu tiên.

$$\begin{gathered} \Rightarrow S=\frac{u_1\left(1-q^{n+1}\right)}{1-q}=\frac{1.\left[1-{\left(\frac{1}{3}\right)}^{n+1}\right]}{1-\frac{1}{3}} \\ =\frac{3}{2}\left[1-{\left(\frac{1}{3}\right)}^{n+1}\right] \end{gathered}$$

Cách 2:

Ta có:

$$\begin{gathered} S=1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}\mathrm{...}+\frac{1}{3^n} \\ \Rightarrow 3S=3+1+\frac{1}{3}+\frac{1}{3^2}+\mathrm{...}+\frac{1}{3^{n-1}} \\ \Rightarrow 3S=3+S-\frac{1}{3^n} \\ \Rightarrow 2S=3-\frac{1}{3^n} \\ \Rightarrow S=\frac{1}{2}.\left(3-\frac{1}{3^n}\right)=\frac{3}{2}\left(1-\frac{1}{3^{n+1}}\right) \end{gathered}$$

Bài tập 1 SGK trang 103 Toán lớp 11 Đại số: Chứng minh các dãy số $\left(\frac{3}{5}{.2}^n\right)$, $\left(\frac{5}{2^n}\right)$, $\left({\left(-\frac{1}{2}\right)}^n\right)$ là các cấp số nhân.

Lời giải:

+ Ta có:  $u_n=\frac{3}{5}{.2}^n$

$u_1=\frac{3}{5}\cdot 2^1=\frac{6}{5}$

Với mọi $\forall n\in \mathbb{N}*$, ta có: $u_{n+1}=\frac{3}{5}\cdot 2^{n+1}$

$$\begin{gathered} \Rightarrow \frac{u_{n+1}}{u_n}=\frac{\frac{3}{5}\cdot 2^{n+1}}{\frac{3}{5}\cdot 2^n} \\ =\frac{2^{n+1}}{2^n}=\frac{2^n\cdot 2}{2^n}=2 \end{gathered}$$ (không đổi)

Vậy dãy số đã cho là một cấp số nhân với $u_1=\frac{6}{5}$ và q = 2.

+ Ta có:  $u_n=\frac{5}{2^n}$

$u_1=\frac{5}{2^1}=\frac{5}{2}$

Với mọi $\forall n\in \mathbb{N}*$, ta có:

 $$\begin{gathered} \frac{u_{n+1}}{u_n}=\frac{\frac{5}{2^{n+1}}}{\frac{5}{2^n}} \\ =\frac{5}{2^{n+1}}:\frac{5}{2^n} \\ =\frac{5}{2^{n+1}}\cdot \frac{2^n}{5} \\ =\frac{2^n}{2^{n+1}} \\ =\frac{2^n}{2^n\cdot 2}=\frac{1}{2}(không đổi) \end{gathered}$$ 

Vậy dãy số đã cho là một cấp số nhân với $u_1=\frac{5}{2}$ và $q=\frac{1}{2}$

+ Ta có: $u_n={\left(-\frac{1}{2}\right)}^n$ suy ra $u_1={\left(-\frac{1}{2}\right)}^1=-\frac{1}{2}$

Với mọi $\forall n\in \mathbb{N}*$, ta có:

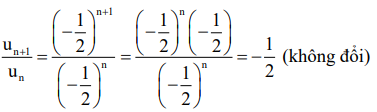
Vậy dãy số đã cho là một cấp số nhân với $u_1=\frac{-1}{2}$ và $q=\frac{-1}{2}$

 

Bài tập 2 SGK trang 103 Toán lớp 11 Đại số: Cho cấp số nhân (u_n) với công bội q.

a) Biết u₁ = 2, u₆ = 486. Tìm q.

b) Biết $q=\frac{2}{3}$, $u_4=\frac{8}{21}$. Tìm u₁.

c) Biết u₁ = 3, q = -2. Hỏi số 192 là số hạng thứ mấy?

Lời giải:

a) Ta có: u₆ = u₁.q⁵

   $\Rightarrow 486=2.q^5 \iff q^5=243 \iff q=3$

b) Ta có: u₄ = u₁.q³

$\Rightarrow \frac{8}{21}=u_1\cdot {\left(\frac{2}{3}\right)}^3 \iff u_1=\frac{9}{7}$

c) Ta có:

u_n = u₁.q^n-1

 $$\begin{gathered} \Rightarrow 192=3.{\left(-2\right)}^{n-1} \\ \iff {\left(-2\right)}^{n-1}=64 \\ \iff n–1=6 \\ \iff n=7 \end{gathered}$$   

Vậy số 192 là số hạng thứ 7.

Bài tập 3 SGK trang 103 Toán lớp 11 Đại số: Tìm các số hạng của cấp số nhân (u_n) có năm số hạng, biết:

a) u₃ = 3 và u₅ = 27;

b) u₄ – u₂ = 25 và u₃ – u₁ = 50.

Lời giải:

a) Ta có:

$$\begin{gathered} \left\{\begin{array}{l}{u}_3=3\\ u_5=27\end{array}\right. \\ \Rightarrow \left\{\begin{array}{l}{u}_1.q^2=3\\ u_1.q^4=27\end{array}\right. \\ \Rightarrow q^2=9 \\ \iff q=\pm 3 \end{gathered}$$

Với q = 3 ta có: $u_1=\frac{1}{3}$. Ta có cấp số nhân:

$u_1=\frac{1}{3}$, u₂ = 1, u₃ = 3, u₄ = 9, u₅ = 27

Với q = -3 ta có: $u_1=\frac{1}{3}$. Ta có cấp số nhân:

$u_1=\frac{1}{3}$, u₂ = -1, u₃ = 3, u₄ = -9, u₅ = 27

b) Ta có:

$$\begin{gathered} \left\{\begin{array}{l}{u}_4-u_2=25\\ u_3-u_1=50\end{array}\right. \\ \iff \left\{\begin{array}{l}{u}_1{q}^3-u_{1}q=25\\ u_1{q}^2-u_1=50\end{array}\right. \\ \iff \left\{\begin{array}{l}{u}_{1}q\left(q^2-1\right)=25\\ u_1\left(q^2-1\right)=50\end{array}\right. \\ \iff \left\{\begin{array}{l}q.50=25\\ u_1\left(q^2-1\right)=50\end{array}\right. \\ \iff \left\{\begin{array}{l}q=\frac{1}{2}\\ u_1\left(\frac{1}{4}-1\right)=50\end{array}\right. \\ \iff \left\{\begin{array}{l}q=\frac{1}{2}\\ u_1=\frac{-200}{3}\end{array}\right. \end{gathered}$$

Ta có năm số hạng của cấp số nhân:

$\frac{-200}{3};\frac{-100}{3};\frac{-50}{3};\frac{-25}{3};\frac{-25}{6}$.

Bài tập 4 SGK trang 104 Toán lớp 11 Đại số: Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62.

Lời giải:

Giả sử có cấp số nhân: u₁, u₂, u₃, u₄, u₅, u₆

Theo giả thiết ta có:

u₁ + u₂ + u₃ + u₄ + u₅ = 31      (1)

u₂ + u₃ + u₄ + u₅ + u₆ = 62      (2)

Nhân hai vế của (1) với q, ta được:

u₁q + u₂q + u₃q + u₄q + u₅q = 31q

$\iff$ u₂ + u₃ + u₄ + u₅ + u₆ = 31q       (3)

Từ (2) và (3) suy ra 62 = 31.q

Suy ra q = 2

Ta có S₅ = 31

 $\iff \frac{u_1\left(1-2^5\right)}{1-2}=31$

$\iff 31u_1=31\iff u_1=1$

Vậy ta có cấp số nhân là: 1, 2, 4, 8, 16, 32.

Cách khác:

Ta có: $S_5=\frac{u_1.\left(1-q^5\right)}{1-q}$

S₅’= u₂ + u₃ + u₄ + u₅ + u₆

= u₁q + u₂q + u₃q + u₄q + u₅q

= q.( u₁ + u₂ + u₃ + u₄ + u₅)

= q. S₅

Mà S₅ = 31, S₅’= 62

Khi đó q = 2

$\Rightarrow u_1=\frac{S_5.\left(1-q\right)}{1-q^5}=1$

Vậy ta có cấp số nhân là 1, 2, 4, 8, 16, 32.

Bài tập 5 SGK trang 104 Toán lớp 11 Đại số: Tỉ lệ tăng dân số của tỉnh X là 1,4%. Biết rằng số dân của tỉnh hiện nay là 1,8 triệu người. Hỏi với mức tăng như vậy thì sau 5 năm, 10 năm số dân của tỉnh đó là bao nhiêu?

Lời giải:

Giả sử số dân của một tỉnh đó hiện nay là N. Vì tỉ lệ tăng dân số là 1,4% nên sau một năm, số dân tăng thêm là 1,4%.N

Vậy số dân của tỉnh đó vào năm sau là

$$\begin{gathered} N+1,4\%.N \\ =101,4\%.N \\ =\frac{101,4}{100}\cdot N \end{gathered}$$

Như vậy số dân của tỉnh đó sau mỗi năm lập thành cấp số nhân. Hiện tại: u₁ = N

Sau 1 năm: $u_2=\frac{101,4}{100}\cdot N$

Sau 2 năm: $u_3={\left(\frac{101,4}{100}\right)}^2\cdot N$; ...

Vậy nếu N = 1,8 triệu người

Áp dụng công thức tính số hạng tổng quát của cấp số nhân thì:

Sau 5 năm số dân của tỉnh là

$u_6={\left(\frac{101,4}{100}\right)}^5\cdot 1,8\approx 1,9$ (triệu người)

Vậy sau 10 năm số dân của tỉnh là

$u_{11}={\left(\frac{101,4}{100}\right)}^{10}\cdot 1,8\approx 2,1$ (triệu người).

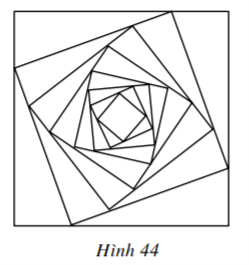
Bài tập 6 SGK trang 104 Toán lớp 11 Đại số: Cho hình vuông C₁ có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C₂ (h.44). Từ hình vuông C₂ lại tiếp tục như trên để được hình vuông C₃,… Tiếp tục quá trình trên, ta nhận được các dãy các hình vuông C₁, C₂, C₃, …,C_n,…

Gọi a_n là độ dài cạnh của hình vuông C_n. Chứng minh dãy số (a_n) là một cấp số nhân.

Lời giải:

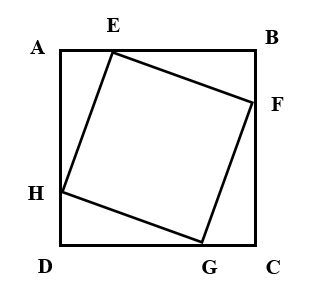
Xét dãy số (a_n), ta có a₁ = 4.

Gọi a_n là cạnh hình vuông C_n.

Ta tính cạnh hình vuông a_n+1 như sau:

Xét tam giác BEF vuông tại B có:

$BE=\frac{3}{4}BA=\frac{3a_n}{4}$, $BF=\frac{1}{4}BC=\frac{a_n}{4}$

Do đó

$$\begin{gathered} EF=\sqrt{B{E}^2+B{F}^2} \\ =\sqrt{{\left(\frac{3a_n}{4}\right)}^2+{\left(\frac{a_n}{4}\right)}^2}=\frac{\sqrt{10}}{4}{a}_n \end{gathered}$$

hay $a_{n+1}=\frac{\sqrt{10}}{4}{a}_n$

Vậy dãy số (a_n) là cấp số nhân với số hạng đầu là a₁ = 4 và công bội $q=\frac{\sqrt{10}}{4}$

Bài giảng Toán 11 Bài 4: Cấp số nhân

Xem thêm lời giải bài tập Toán lớp 11 hay, chi tiết khác:

Ôn tập chương 3

Bài 1: Phép biến hình

Bài 2: Phép tịnh tiến

Bài 3: Phép đối xứng trục

Bài 4: Phép đối xứng tâm

Xem thêm tài liệu Toán lớp 11 hay, chi tiết khác:

Lý thuyết Cấp số nhân

Lý thuyết Cấp số nhân