Nội dung bài viết

    Xem thêm

    Toán 11 Bài 3: Cấp số cộng

    Với giải bài tập Toán lớp 11 Bài 3: Cấp số cộng chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11.

    1 1,419 03/11/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải Toán 11 Bài 3: Cấp số cộng

    Video giải Toán 11 Bài 3: Cấp số cộng

    Hoạt động 1 trang 93 SGK Toán lớp 11 Đại số: Biết bốn số hạng đầu của một dãy số là -1, 3, 7, 11. Từ đó chỉ ra một quy luật rồi viết tiếp năm số hạng của dãy theo quy luật đó.

    Lời giải:

    Ta có:

    3 = -1 + 4

    7 = 3 + 4

    11 = 7 + 4

    Quy luật: kể từ số thứ 2, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với 4.

    Năm số hạng tiếp của dãy theo quy luật đó là: 15; 19; 23; 27; 31.

    Hoạt động 2 trang 93 SGK Toán lớp 11 Đại số: Cho (un) là một cấp số cộng có sáu số hạng với u1=−13, d = 3. Viết dạng khai triển của nó.

    Lời giải:

    Ta có:

    u2=u1+d=−13+3=83u3=u2+d=83+3=173u4=u3+d=173+3=263u5=u4+d=263+3=353u6=u5+d=u5+3=353+3=443

    Dạng khai triển của cấp số cộng đó là:

     −13;83;173;263;353;443

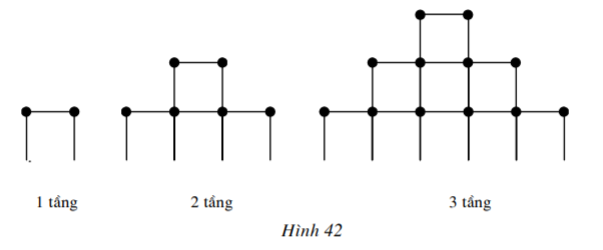
    Hoạt động 3 trang 94 SGK Toán lớp 11 Đại số: Mai và Hùng chơi trò xếp các que diêm thành hình tháp trên mặt sân. Cách xếp được thể hiện trên Hình 42.

    Nếu tháp có 100 tầng thì cần bao nhiêu que diêm để xếp tầng đế của tháp (ảnh 1)

    Hỏi: Nếu tháp có 100 tầng thì cần bao nhiêu que diêm để xếp tầng đế của tháp?

    Lời giải:

    Xây 1 tầng cần 2 que diêm để xếp tầng đế

    Xây 2 tầng cần 4 que diêm để xếp tầng đế (4 = 2 + 1.2)

    Xây 3 tầng cần 6 que diêm để xếp tầng đế (6 = 2 + 2.2)

    Xây 100 tầng cần 200 que diêm để xếp tầng đế (200 = 2 + 99.2)

    Hoạt động 4 trang 96 SGK Toán lớp 11 Đại số: Cấp số cộng gồm tám số hạng -1, 3, 7, 11, 15, 19, 23, 27 được viết vào bảng sau:

    -1

    3

    7

    11

    15

    19

    23

    27

     

     

     

     

     

     

     

     

    a) Hãy chép lại bảng trên và viết các số hạng của cấp số đó vào dòng thứ hai theo thứ tự ngược lại. Nêu nhận xét về tổng của các số hạng ở mỗi cột.

    b) Tính tổng các số hạng của cấp số cộng.

    Lời giải:

    a)

    -1

    3

    7

    11

    15

    19

    23

    27

     27

    23

    19 

    15 

    11 

     7

     3

    -1 

    Tổng các số hạng của từng cột bằng nhau và bằng 26.

    b) Tổng các số hạng của cấp số cộng là: 26.82=104

    Bài tập 1 trang 97 SGK Toán lớp 11 Đại số: Trong các dãy số (un) sau đây, dãy số nào là cấp số cộng? Tính số hạng đầu và công sai của nó.

    a) un = 5 – 2n

    b) un=n2−1

    c) un = 3n

    d) un=7−3n2

    Lời giải:

    a) Ta có:

    u1 = 5 – 2.1 = 3

    un+1 – un = 5 – 2(n + 1) – 5 + 2n

    = 5 – 2n – 2 – 5 + 2n =  – 2 ∀n∈ℕ*

    Suy ra un+1 = un – 2 

    Vậy (un) là cấp số cộng có u1 = 3, công sai d = – 2

    b) Ta có: u1=12−1=−12

    un+1–un=n+12−1−n2+1 

    =n+12−n2=12, ∀n∈ℕ*

    Suy ra un+1=un+12,∀n∈ℕ*

    Vậy (un) là cấp số cộng có u1=−12, công sai d=12.

    c) Ta có

    un+1 – un = 3n+1 – 3n = 3. 3n – 3n = 2.3n

    Vậy (un) không là cấp số cộng.

    Cách khác:

    un = 3n  suy ra u1 = 3

    Giả sử n≥1, xét hiệu sau:

    un+1 – un = 3n+1 – 3n

    = 3. 3n – 3n = 2.3n

    un – un-1 = 3n – 3n-1

    = 3. 3n-1 = (3 – 1).3n-1 = 2.3n-1

    Suy ra un+1–un≠un–un−1 (vì 3n≠3n−1,∀n)

    Vậy (un) không là cấp số cộng.

    d) Ta có: u1=7−3.12=2

    Với mọi n∈ℕ* ta có:

    un+1−un=7−3n+12−7−3n2=7−3n−3−7+3n2=−32

    Suy ra un+1=un−32,∀n∈ℕ*

    Vậy (un) là cấp số cộng có u1 = 2, công sai d=−32.

    Bài tập 2 trang 97 SGK Toán lớp 11 Đại số: Tìm số hạng đầu và công sai của cấp số cộng sau, biết:

    a) u1−u3+u5=10u1+u6=17

    b) u7−u3=8u2.u7=75

    Lời giải:

    a) Ta có : 

    u3 = u1 + 2d ;

    u5 = u1 + 4d ;

    u6 = u1 + 5d

    Theo đề bài ta có :

    u1−u3+u5=10u1+u6=17⇔u1−u1+2d+u1+4d=10u1+u1+5d=17⇔u1+2d=102u1+5d=17 ⇔u1=16d=−3

    Vậy số hạng đầu và công sai của cấp số cộng là u1 = 16, d = -3.

    b) Ta có:

    u7 = u1 + 6d

    u3 = u1 + 2d

    u2 = u1 + d

    Do đó theo đề bài ta có:

    u7−u3=8u2.u7=75 ⇔u1+6d−u1−2d=8u1+du1+6d=75⇔4d=8u1+du1+6d=75⇔d=2u1+2u1+12=75⇔d=2u12+14u1+24=75⇔d=2u12+14u1−51=0⇔d=2u1=3u1=−17

    Vậy u1 = 3, công sai d = 2 hoặc u1 = -17, công sai d = 2 là số hạng đầu và công sai của cấp số cộng.

    Bài tập 3 trang 97 SGK Toán lớp 11 Đại số: Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng u1, d, n, un, Sn.

    a) Hãy viết các hệ thức liên hệ giữa các đại lượng đó. Cần phải biết ít nhất mấy đại lượng để có thể tìm được các đại lượng còn lại?

    b) Lập bảng theo mẫu sau và điền số thích hợp vào ô trống:

    u1

    d

    n

    un

    Sn

    -2

     

     55

     20

     

     

     -4

     

     15

     120

    3

    		 427

     7

     

     

     

     

     17

     12

     72

    2

    -5

     

     

    -205 

    Lời giải:

    a) Ta có: un = u1 + (n – 1).d

    ⇒n=un−u1 d+1;d=un−u1n−1

    Ta có: 

    Sn=n.u1+n(n−1)2 d=nu1+un2⇒u1=2.Sn−n(n−1).d2n

    Hay u1=2 Sn−n.unn

    Dựa vào các công thức trên thấy cần phải biết ít nhất 3 đại lượng để tìm được các đại lượng còn lại.

    b) Dòng đầu: Biết u1= −2; u20 = 55. Tìm d và S20.

    Ta có u20 = u1 + 19d

    ⇔55=−2+19d⇔d=3

    S20=20u1+u202=20.−2+552=530

    Dòng 2: Biết d = −4; S15 = 120 , tìm u1 và u15.

    Ta có 

    S15=15u1+15.15−12.d⇔120=15.u1+105.−4 ⇔15u1=540 ⇔u1=36   

    Suy ra u15 = u1 + 14d = 36 + 14.(−4) = −20

    Dòng 3: Biết u1 = 3; d = ; un = 7. Tìm n và tính Sn.

    Ta có un = u1 + (n − 1)d

    ⇔7=3+n−1.427 ⇔n=28

    S28=28u1+28.28−12.d =28.3+378.427=140

    Dòng 4: Biết u12 = 17 và S12 = 72. Tìm u1 và d.

    S12=12u1+u122 ⇔72=12u1+172⇔u1+17=12 ⇔u1=−5

    u12 = u1 + 11d

    ⇔17=−5+11d ⇔22 =11d  ⇔d=2

    Dòng 5: Biết u1 = 2; d = −5 và Sn = −205. Tìm n và tính un.

    Ta có:

    Sn=nu1+nn−12d⇔−205=n.2+nn−12.(−5)⇔−410=4n−5nn−1⇔5n2−9n–410=0⇔n=10n=−415loại

    Suy ra n = 10

    Suy ra u10 = u1 + 9d = 2 + 9.(−5) = −43

    Vậy ta điền được bảng như sau :

    u1

    d

    n

    un

    Sn

    -2

    3

    55

    20

    530

    36

    -4

    -20

    15

    120

    3

    		 427

    7

    28

    140

    -5

    2

    17

    12

    72

    2

    -5

    -43

    10

    -205

    Bài tập 4 trang 98 SGK Toán lớp 11 Đại số: Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân 0,5 m. Cầu thang đi từ tầng một lên tầng hai gồm 21 bậc, mỗi bậc cao 18 cm.

    a) Viết công thức để tìm độ cao của một bậc tùy ý so với mặt sân.

    b) Tính độ cao của sàn tầng hai so với mặt sân.

    Lời giải:

    a) Mỗi bậc thang cao 18cm = 0,18m

    Suy ra n bậc thang cao 0,18n (m)

    Vì mặt sàn cao hơn mặt sân 0,5 m nên công thức tính độ cao của một bậc tùy ý so với mặt sân sẽ là :

    hn = 0,5 + 0,18n

    b) Độ cao của sàn tầng hai so với mặt sân ứng với n = 21 là:

    h21 = 0,5 + 0,18.21 = 4,28 (m)

    Bài tập 5 trang 98 SGK Toán lớp 11 Đại số: Từ 0 giờ đến 12 giờ trưa, đồng hồ đánh bao nhiêu tiếng, nếu nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?

    Lời giải:

    Lúc 1 giờ đồng hồ đánh 1 tiếng chuông.

    Lúc 2 giờ đồng hồ đánh 2 tiếng chuông

    ......

    Lúc 12 giờ trưa đồng hồ đánh 12 tiếng chuông.

    Do đó, từ 0 giờ đến 12 giờ trưa, đồng hồ đánh số tiếng chuông là:

    S = 1 + 2 + 3 +....+ 12

    Đây là tổng của 12 số hạng của cấp số cộng có u1 = 1, u12 = 12.

    Do đó áp dụng công thức tính tổng của cấp số cộng ta có

     S=1+12.122=78  

    Vậy đồng hồ đánh 78 tiếng chuông.

    Bài giảng Toán 11 Bài 3: Cấp số cộng

    Xem thêm lời giải bài tập Toán lớp 11 hay, chi tiết khác:

    Bài 4: Cấp số nhân

    Ôn tập chương 3

    Bài 1: Phép biến hình

    Bài 2: Phép tịnh tiến

    Bài 3: Phép đối xứng trục

    Xem thêm tài liệu Toán lớp 11 hay, chi tiết khác:

    Lý thuyết Cấp số cộng

    Trắc nghiệm Cấp số cộng có đáp án

    •  

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,419 03/11/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: