Nội dung bài viết

    Xem thêm

    Toán 11 Bài 1: Quy tắc đếm

    Với giải bài tập Toán lớp 11 Toán 11 Bài 1: Quy tắc đếm chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11.

    1 1,639 20/10/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải Toán 11 Bài 1: Quy tắc đếm

    Video giải Toán 11 Bài 1: Quy tắc đếm

    Hoạt động 1 trang 44 SGK Toán lớp 11 Đại số: Trong ví dụ 1, kí hiệu A là tập hợp các quả cầu trắng, B là tập hợp các quả cầu đen. Nêu mối quan hệ giữa số cách chọn một quả cầu và số các phần tử của hai tập A, B.
    Lời giải:

    Số cách chọn một quả cầu bằng tổng số các phần tử của hai tập hợp A, B.

    Hoạt động 2 trang 45 SGK Toán lớp 11 Đại số: Từ thành phố A đến thành phố B có ba con đường, từ B đến C có bốn con đường (Hình 25). Hỏi có bao nhiêu cách đi từ A đến C, qua B?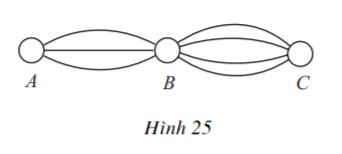Từ thành phố A đến thành phố B có ba con đường, từ B đến C có bốn con đường (ảnh 1)

    Lời giải:

    Từ A đến B có 3 cách

    Từ B đến C có 4 cách

    Áp dụng quy tắc nhân ta có: 3.4 = 12 cách đi từ A đến C, qua B

    Vậy có 12 cách đi từ A đến C, qua B.

    Bài 1 trang 46 SGK Toán lớp 11 Đại số: Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm:

    a) Một chữ số?

    b) Hai chữ số?

    c) Hai chữ số khác nhau?

    Lời giải:

    a) Có 4 số tự nhiên có một chữ số lập được từ các chữ số 1, 2, 3, 4.

    b) Gọi số có 2 chữ số là ab¯ 

    a có 4 cách chọn

    b có 4 cách chọn

    Vậy theo quy tắc nhân có 4.4 = 16 số.

    c) Gọi số có 2 chữ số khác nhau có dạng ab¯ (a≠b)

    a có 4 cách chọn

    b có 3 cách chọn (do a ≠ b)

    Vậy theo quy tắc nhân có 4.3 = 12 số.

    Bài 2 trang 46 SGK Toán lớp 11 Đại số: Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?

    Lời giải:

    Trường hợp 1: có 6 số tự nhiên có 1 chữ số lập từ 1, 2, 3, 4, 5, 6.

    Trường hợp 2: từ 1, 2, 3, 4, 5, 6 lập số tự nhiên có hai chữ số.

    Gọi số tự nhiên có 2 chữ số là ab¯ (a≠0)

    Có 6 cách chọn chữ số a

    Có 6 cách chọn chữ số b

    Áp dụng quy tắc nhân có 62 = 36 số tự nhiên có hai chữ số lập được từ các chữ số 1, 2, 3, 4, 5, 6.

    Vậy quy tắc cộng có 6 + 36 = 42 (số)

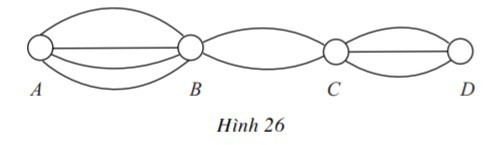
    Bài 3 trang 46 SGK Toán lớp 11 Đại số: Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình 26. Hỏi:

    a) Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?

    b) Có bao nhiêu cách đi từ A đến D rồi quay lại A?

    Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình 26 (ảnh 1)

    Lời giải:

    a) Để đi từ A đến D mà qua B và C chỉ một lần, phải thực hiện liên tiếp ba hành động sau đây:

    Hành động 1: Đi từ A đến B. Có 4 cách để thực hiện hành động này.

    Hành động 2: Đi từ B đến C. Có 2 cách để thực hiện hành động này.

    Hành động 3: Đi từ C đến D. Có 3 cách để thực hiện hành động này.

    Theo quy tắc nhân, số các cách để đi từ A đến D mà qua B và C chỉ một lần là 4.2.3 = 24 (cách).

    Vậy có 24 cách để đi từ A đến D mà qua B và C chỉ một lần.

    b) Khi đi từ A đến D rồi quay về A nghĩa là công việc được thực hiện qua 2 hành động:

    Từ A đến D qua B, C chỉ 1 lần có 24 cách.

    Từ D về A qua C, B chỉ 1 lần có 24 cách.

    Áp dụng quy tắc nhân, số các cách để đi từ A đến D (mà qua B và C chỉ một lần), rồi quay lại A (mà qua C và B chỉ một lần) là: 24.24 = 576 (cách).

    Vậy có 576 cách đi từ A đến D rồi quay lại A.

    Bài 4 trang 46 SGK Toán lớp 11 Đại số: Có ba hiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?

    Lời giải:

    Theo bài ra, ta có:

    3 cách chọn kiểu mặt đồng hồ.

    4 cách chọn kiểu dây.

    Theo quy tắc nhân, có 3.4 = 12 cách

    Vậy có 12 cách chọn một chiếc đồng hồ gồm một mặt và một dây.

    Bài giảng Toán 11 Bài 1: Quy tắc đếm

    Xem thêm lời giải bài tập Toán lớp 11 Đại số và Giải tích hay, chi tiết khác:

    Bài 2: Hoán vị - chỉnh hợp – tổ hợp

    Bài 3: Nhị thức Niu-tơn

    Bài 4: Phép thử và biến cố

    Bài 5: Xác suất của biến cố

    Ôn tập chương 2

    Xem thêm tài liệu Toán lớp 11 Đại số và Giải tích hay, chi tiết khác:

    Lý thuyết Quy tắc đếm

    Trắc nghiệm Quy tắc đếm có đáp án

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,639 20/10/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: