Toán 11 Bài 3: Một số phương trình lượng giác thường gặp

Mục lục Giải Toán 11 Bài 3: Một số phương trình lượng giác thường gặp

Video giải Toán 11 Bài 3: Một số phương trình lượng giác thường gặp

Hoạt động 1 trang 29 SGK Toán lớp 11 Đại số: Giải các phương trình sau

a) 2sinx − 3 = 0 là phương trình bậc nhất đối với sinx.

b) $\sqrt{3}\tan x+1=0$ là phương trình bậc nhất đối với tanx.

Lời giải:

a) 2sinx – 3 = 0

 $\iff sinx=\frac{3}{2}$

Phương trình vô nghiệm vì $\sin x\le 1<\frac{3}{2}$  với mọi x.

b) $\sqrt{3}\tan x+1=0$

$\iff \tan x=\frac{-\sqrt{3}}{3}$

 $\iff \tan x=\tan \frac{-\pi }{6}$

 $\iff x=\frac{-\pi }{6}+k\pi ,k\in \mathbb{Z}$

Vậy các nghiệm của phương trình là $x=\frac{-\pi }{6}+k\pi ,k\in \mathbb{Z}$ .

Hoạt động 2 trang 31 SGK Toán lớp 11 Đại số: Giải các phương trình sau:

a) 3cos²x − 5cos x + 2 = 0 ;

b) $3ta{n}^{2}3-2\sqrt{3}\tan x+3=0$.

Lời giải:

a) 3cos²x – 5cosx + 2 = 0

Đặt cosx = t với điều kiện -1 ≤ t ≤ 1 (*), ta được phương trình bậc hai theo t:

3t² - 5t + 2 = 0 (1)

Δ = (-5)² - 4.3.2 = 1

Phương trình (1) có hai nghiệm là: 

$t_1=\frac{-(-5)+\sqrt{1}}{2.3}=\frac{6}{6}=1$ (thỏa mãn)

$t_2=\frac{-(-5)-\sqrt{1}}{2.3}=\frac{4}{6}=\frac{2}{3}$ (thỏa mãn)

Trường hợp 1: cosx = 1

$\iff x=k2\pi ,k\in \mathbb{Z}$

Trường hợp 2: $\cos x=\frac{2}{3}$$\iff x=\pm \arccos \frac{2}{3}+k2\pi ,\text{ k}\in \mathbb{Z}$

Vậy các nghiệm của phương trình là $x=k2\pi ;x=\pm \arccos \frac{2}{3}+k2\pi ,k\in \mathbb{Z}$.

b) $3{\tan }^{2}x-2\sqrt{3}\tan x+3=0$

Đặt tanx = t, ta được phương trình bậc hai theo t:

$3t^2-2\sqrt{3}t+3=0\left(1\right)$

$\Delta ={(-2\sqrt{3})}^2-\mathrm{4.3.3}=-24<0$

Vậy phương trình (1) vô nghiệm, nên không có $x$ thỏa mãn đề bài.

Hoạt động 3 trang 32 SGK Toán lớp 11 Đại số: Hãy nhắc lại:

a) Các hằng đẳng thức lượng giác cơ bản;

b) Công thức cộng;

c) Công thức nhân đôi;

d) Công thức biến đổi tích thành tổng và tổng thành tích.

Lời giải:

a) Các hằng đẳng thức lượng giác cơ bản:

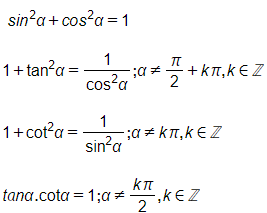
b) Công thức cộng:

cos(a - b) = cosa.cosb + sina.sinb

cos(a + b) = cosa.cosb - sina.sinb

sin(a + b) = sina.cosb + cosa.sinb

sin(a - b) = sina.cosb - cosa.sinb

$\tan (a-b)=\frac{\tan a-\tan b}{1+\tan a.\tan b}$

$\tan (a+b)=\frac{\tan a+\tan b}{1-\tan a.\tan b}$

c) Công thức nhân đôi:

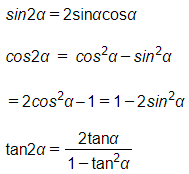
d) Công thức biến đổi tích thành tổng:

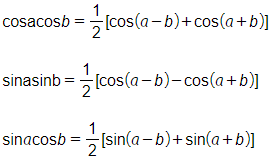
Công thức biến đổi tổng thành tích:

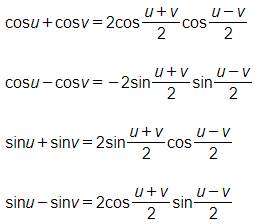
Hoạt động 4 trang 34 SGK Toán lớp 11 Đại số: Giải phương trình

3cos²6x + 8sin3xcos3x – 4 = 0.

Lời giải:

3cos²6x + 8sin3xcos3x – 4 =  0

⇔ 3(1 – sin²6x) + 4sin 6x – 4 = 0 (áp dụng hằng đẳng thức và công thức nhân đôi)

⇔ –3sin²6x + 4sin6x – 1 = 0

Đặt sin 6x = t với điều kiện $-1\le t\le 1$ (*), ta được phương trình bậc hai theo t:

$-3t^2+4t-1=0\left(1\right)$

$\Delta =4^2-4.(-1).(-3)=4$

Phương trình (1) có hai nghiệm là:

$t_1=\frac{-4+\sqrt{4}}{2\cdot (-3)}=\frac{1}{3}\left(TM\right)$

$t_2=\frac{-4-\sqrt{4}}{2\cdot (-3)}=1\left(TM\right)$

Ta có:

Trường hợp 1:

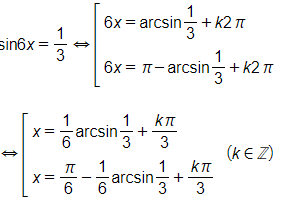
Trường hợp 2: sin6x = 1

$\iff \sin 6x=\sin \frac{\pi }{2}$

$\iff 6x=\frac{\pi }{2}+k2\pi$

$\iff x=\frac{\pi }{12}+\frac{k\pi }{3},k\in \mathbb{Z}$

Vậy nghiệm của phương trình là: $x=\frac{\pi }{12}+\frac{k\pi }{3}$, $x=\frac{1}{6}\arcsin \frac{1}{3}+\frac{k\pi }{3}$,

$x=\frac{\pi }{6}-\frac{1}{6}\arcsin \frac{1}{3}+\frac{k\pi }{3}\left(k\in \mathbb{Z}\right)$.

Hoạt động 5 trang 35 SGK Toán lớp 11 Đại số: Dựa vào công thức cộng đã học:

sin (a + b) = sinacosb + sinbcosa  

cos (a + b) = cosacosb − sinasinb 

sin (a − b) = sinacosb − sinbcosa

cos (a − b) = cosacosb + sinasinb

và kết quả $\cos \frac{\pi }{4}=\sin \frac{\pi }{4}=\frac{\sqrt{2}}{2}$ , hãy chứng minh rằng:

a)  $\sin x+\cos x=\sqrt{2}\cos \left(x-\frac{\pi }{4}\right)$;

b) $\sin x-\cos x=\sqrt{2}\sin \left(x-\frac{\pi }{4}\right)$.

Lời giải:

a) $\sin x+\cos x=\sqrt{2}\cos \left(x-\frac{\pi }{4}\right)$

Ta có:

 

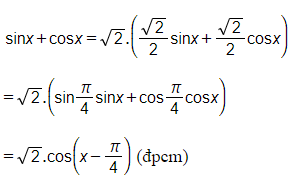
Cách khác:

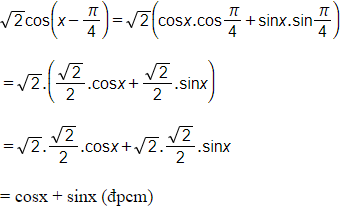
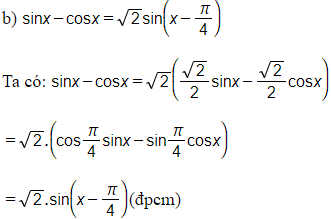
Cách khác:

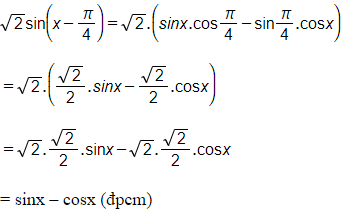
Hoạt động 6 trang 36 SGK Toán lớp 11 Đại số: Giải phương trình:  $\sqrt{3}\sin 3x-\cos 3x=\sqrt{2}$

Lời giải:

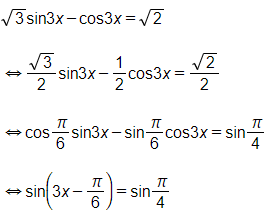
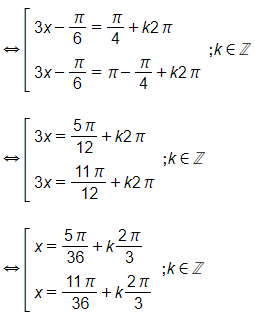
Vậy các nghiệm của phương trình là $x=\frac{5\pi }{36}+k\frac{2\pi }{3};x=\frac{11\pi }{36}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$.

Bài 1 trang 36 SGK Toán lớp 11 Đại số: Giải phương trình: sin²x – sinx = 0.

Lời giải:

 ${\sin }^{2}x-\sin x=0$

$\iff \sin x(\sin x-1)=0$

$\iff \left[\begin{array}{l}\sin x=0\\ \sin x-1=0\end{array}\right.$

$\iff \left[\begin{array}{l}\sin x=0\\ \sin x=1\end{array}\right.$

$\iff \left[\begin{array}{l}x=k\pi \\ x=\frac{\pi }{2}+k2\pi \end{array}(k\in \mathbb{Z})\right.$

Vậy nghiệm của phương trình là $x=k\pi$; $x=\frac{\pi }{2}+k2\pi (k\in \mathbb{Z})$.

Bài 2 trang 36 SGK Toán lớp 11 Đại số: Giải các phương trình sau:

a) 2cos²x – 3cosx +1 = 0;

b) $2\sin 2x+\sqrt{2}\sin 4x=0$.

Lời giải:

a) 2cos²x – 3cosx + 1 = 0

Đặt $\cos x=t(-1\le t\le 1)$

Phương trình trở thành: 2t² – 3t +1 = 0

$\iff \left[\begin{array}{l}t=1\text{ (TM) }\\ t=\frac{1}{2}\text{(TM) }\end{array}\right.$

Với t = 1 $\Rightarrow cosx=1$ $\iff x=k2\pi ,k\in \mathbb{Z}$

Với  $t=\frac{1}{2}$ $\Rightarrow \cos x=\frac{1}{2}$ $\iff x=\pm \frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$

Vậy các nghiệm của phương trình là $x=k2\pi ;x=\pm \frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

b) $2\sin 2x+\sqrt{2}\sin 4x=0$

$\iff 2\sin 2x+2\sqrt{2}\sin 2x\cos 2x=0$

$\iff 2\sin 2x\left(1+\sqrt{2}\cos 2x\right)=0$

$\iff \left[\begin{array}{l}\sin 2x=0\\ 1+\sqrt{2}\cos 2x=0\end{array}\right.$

$\iff \left[\begin{array}{l}\sin 2x=0\\ \cos 2x=-\frac{1}{\sqrt{2}}\end{array}\right.$

$\iff \left[\begin{array}{l}2x=k\pi \\ 2x=\pm \frac{3\pi }{4}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=\frac{k\pi }{2}\\ x=\pm \frac{3\pi }{8}+k\pi \end{array}\right.(k\in \mathbb{Z})$

Vậy nghiệm của phương trình là $x=\frac{k\pi }{2}$; $x=\pm \frac{3\pi }{8}+k\pi (k\in \mathbb{Z})$.

Bài 3 trang 37 SGK Toán lớp 11 Đại số: Giải các phương trình sau:

a)  ${\sin }^2\frac{x}{2}-2\cos \frac{x}{2}+2=0$;

b) 8cos²x + 2sinx – 7 = 0;

c) 2tan²x + 3tanx +1 = 0;

d) tanx – 2cotx + 1 = 0.

Lời giải:

a)  ${\sin }^2\frac{x}{2}-2\cos \frac{x}{2}+2=0$

Ta có: ${\sin }^2\frac{x}{2}=1-{\cos }^2\frac{x}{2}$

Phương trình tương đương với:

$1-{\cos }^2\frac{x}{2}-2\cos \frac{x}{2}+2=0(*)$

$\iff {\cos }^2\frac{x}{2}+2\cos \frac{x}{2}-3=0$

Đặt  $\cos \frac{x}{2}=t\text{ (-1}\le t\le \text{1)}$

Phương trình trở thành:

t² +2t - 3 = 0

$\iff \left[\begin{array}{l}t=1\left(TM\right)\\ t=-3\text{ (L)}\end{array}\right.$

Với t = 1 $\Rightarrow \cos \frac{x}{2}=1$ $\iff \frac{x}{2}=k2\pi$ $\iff x=k4\pi \text{ (k}\in \mathbb{Z})$ 

Vậy nghiệm của phương trình là $x=k4\pi \text{ (k}\in \mathbb{Z})$.

b) 8cos²x + 2sinx – 7 = 0

Ta có: cos²x = 1 – sin²x

Phương trình tương đương với:

8(1 – sin²x) + 2sinx – 7 = 0

$\iff 8si{n}^{2}x–2sinx–1=0$

Đặt sinx = t,  $(-1\le t\le 1)$

Phương trình trở thành: 8t² – 2t – 1 = 0

$\iff \left[\begin{array}{l}t=\frac{1}{2}\left(TM\right)\\ t=\frac{-1}{4}\left(TM\right)\end{array}\right.$

Với  $t=\frac{1}{2}\Rightarrow \sin x=\frac{1}{2}$ $\iff \left[\begin{array}{l}x=\frac{\pi }{6}+k2\pi \\ x=\frac{5\pi }{6}+k2\pi \end{array}\right.(k\in \mathbb{Z})$

Với  $t=\frac{-1}{4}\Rightarrow \sin x=\frac{-1}{4}$ $\iff \left[\begin{array}{l}x=\arcsin \frac{-1}{4}+k2\pi \\ x=\pi -\arcsin \frac{-1}{4}+k2\pi \end{array}\right.(k\in \mathbb{Z})$

Vậy các nghiệm của phương trình là

$$\begin{gathered} x=\frac{\pi }{6}+k2\pi ; \\ x=\frac{5\pi }{6}+k2\pi ; \\ x=\arcsin \frac{-1}{4}+k2\pi ; \\ x=\pi -\arcsin \frac{-1}{4}+k2\pi (k\in \mathbb{Z}) \end{gathered}$$

c) 2tan²x + 3tanx +1 = 0

Điều kiện: $x\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$

Đặt tanx = t, phương trình trở thành:

2t² + 3t +1 = 0

$\iff \left[\begin{array}{l}t=-1\\ t=\frac{-1}{2}\end{array}\right.$

$\iff \left[\begin{array}{l}\tan x=-1\\ \tan x=\frac{-1}{2}\end{array}\right.$

$\iff \left[\begin{array}{l}x=\frac{-\pi }{4}+k\pi \\ x=\arctan \left(\frac{-1}{2}\right)+k\pi \end{array}\right.(k\in \mathbb{Z})$

Vậy các nghiệm của phương trình là $x=\frac{-\pi }{4}+k\pi ;x=\arctan \left(\frac{-1}{2}\right)+k\pi \left(k\in \mathbb{Z}\right)$.

d) tanx – 2cotx + 1 = 0

Điều kiện:  $\left\{\begin{array}{l}\sin x\ne 0\\ \cos x\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x\ne k\pi \\ x\ne \frac{\pi }{2}+k\pi \end{array}\right.\iff x\ne \frac{k\pi }{2}(k\in \mathbb{Z})$

Ta có: tanx – 2cotx + 1 = 0

$\iff \tan x-\frac{2}{\tan x}+1=0$

$\Rightarrow ta{n}^{2}x+tanx–2=0$

Đặt tanx = t, phương trình trở thành:

t² + t – 2 = 0  $\iff \left[\begin{array}{l}t=1\\ t=-2\end{array}\right.$ $\iff \left[\begin{array}{l}\tan x=1\\ \tan x=-2\end{array}\right.$

$\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k\pi \\ x=\arctan (-2)+k\pi \end{array}\right.(k\in \mathbb{Z})$ (Thỏa mãn)

Vậy nghiệm của phương trình là: $x=\frac{\pi }{4}+k\pi$, $x=\arctan (-2)+k\pi ,(k\in \mathbb{Z})$

Bài 4 trang 37 SGK Toán lớp 11 Đại số: Giải các phương trình sau:

a) 2sin²x + sinxcosx − 3cos² x = 0;

b) 3sin²x − 4sinxcosx + 5cos²x = 2;

c) $si{n}^{2}x+sin2x-2co{s}^{2}x=\frac{1}{2}$;

d) $2{\cos }^{2}x-3\sqrt{3}\sin 2x-4{\sin }^{2}x=-4$.

Lời giải:

a) 2sin²x + sinxcosx − 3cos² x = 0

Trường hợp 1: $\cos x=0\iff {\sin }^{2}x=1$

Khi đó ta có 2.1 + 0 – 0 = 0 (vô lý)

Trường hợp 2: $\cos x\ne 0\Rightarrow x\ne \frac{\pi }{2}+k\pi ,(k\in \mathbb{Z})$

Chia cả hai vế của phương trình cho cos²x ta được:

$$\begin{gathered} \frac{{\sin }^{2}x}{{\cos }^{2}x}+\frac{\sin x}{\cos x}-3=0 \\ \iff 2{\tan }^{2}x+\tan x-3=0 \end{gathered}$$

Đặt t = tanx, khi đó phương trình trở thành: $2t^2+t-3=0\iff \left[\begin{array}{l}t=1\\ t=-\frac{3}{2}\end{array}\right.$

Với t = 1 $\Rightarrow \tan x=1\iff x=\frac{\pi }{4}+k\pi ,(k\in \mathbb{Z})$ (Thỏa mãn)

Với $t=-\frac{3}{2}\Rightarrow \tan x=-\frac{3}{2}$ $\iff x=\arctan \left(-\frac{3}{2}\right)+k\pi ,(k\in \mathbb{Z})$  (Thỏa mãn)

Vậy các nghiệm của phương trình là $x=\frac{\pi }{4}+k\pi ,(k\in \mathbb{Z})$; $x=\arctan \left(-\frac{3}{2}\right)+k\pi ,(k\in \mathbb{Z})$.

b) 3sin²x − 4sinxcosx + 5cos²x = 2

Trường hợp 1: $\cos x=0\iff {\sin }^{2}x=1$

Khi đó ta có 3.1 + 0 – 0 = 2 (vô lý)

Trường hợp 2: $\cos x\ne 0\Rightarrow x\ne \frac{\pi }{2}+k\pi ,(k\in \mathbb{Z})$

Chia cả hai vế của phương trình cho cos²x ta được:

$3\frac{{\sin }^{2}x}{{\cos }^{2}x}-4\frac{\sin x}{\cos x}+5=\frac{2}{{\cos }^{2}x}$

$\iff 3{\tan }^{2}x-4\tan x+5=2\left({\tan }^{2}x+1\right)$

$\iff {\tan }^{2}x-4\tan x+3=0$

Đặt t = tanx, khi đó phương trình trở thành: $t^2-4t+3=0\iff \left[\begin{array}{l}t=1\\ t=3\end{array}\right.$

Với t = 1 $\Rightarrow \tan x=1$ $\iff x=\frac{\pi }{4}+k\pi ,(k\in \mathbb{Z})\left(tm\right)$

Với t = 3 $\Rightarrow \tan x=3$ $\iff x=\arctan 3+k\pi ,(k\in \mathbb{Z})\left(tm\right)$

Vậy các nghiệm của phương trình là $x=\frac{\pi }{4}+k\pi ,(k\in \mathbb{Z})$; $x=\arctan 3+k\pi ,(k\in \mathbb{Z})$.

c)  $si{n}^{2}x+sin2x-2co{s}^{2}x=\frac{1}{2}$

$\iff {\sin }^{2}x+2\sin x\cos x-2{\cos }^{2}x=\frac{1}{2}$

$\iff 2{\sin }^{2}x+4\sin x\cos x-4{\cos }^{2}x=1$

Trường hợp 1: $\cos x=0\iff {\sin }^{2}x=1$

Khi đó ta có: 2 + 0 – 0 = 1 (vô nghiệm)

Trường hợp 2: $\cos x\ne 0\Rightarrow x\ne \frac{\pi }{2}+k\pi ,(k\in \mathbb{Z})$

Chia cả hai vế của phương trình cho cos²x ta được:

$2\frac{{\sin }^{2}x}{{\cos }^{2}x}+4\frac{\sin x}{\cos x}-4=\frac{1}{{\cos }^{2}x}$

$\iff 2{\tan }^{2}x+4\tan x-4={\tan }^{2}x+1$

$\iff {\tan }^{2}x+4\tan x-5=0$

Đặt t = tanx, khi đó phương trình trở thành: $t^2+4t-5=0\iff \left[\begin{array}{l}t=1\\ t=-5\end{array}\right.$

Với t = 1 

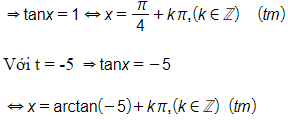
Vậy các nghiệm của phương trình là $x=\frac{\pi }{4}+k\pi ,(k\in \mathbb{Z})$;  $x=\arctan (-5)+k\pi ,(k\in \mathbb{Z})$

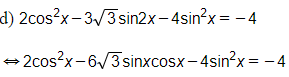
Trường hợp 1: $\cos x=0\iff {\sin }^{2}x=1$

Khi đó ta  0 + 0 - 4 = - 4 (Luôn đúng)

$\Rightarrow x=\frac{\pi }{2}+k\pi ,(k\in \mathbb{Z})$ là nghiệm của phương trình.

Trường hợp 2: $\cos x\ne 0\Rightarrow x\ne \frac{\pi }{2}+k\pi ,(k\in \mathbb{Z})$

Chia cả hai vế của phương trình cho  ta được:

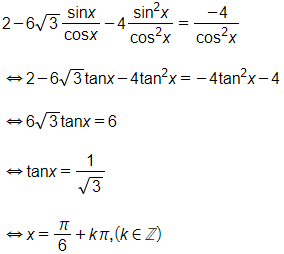
Vậy các nghiệm của phương trình là $x=\frac{\pi }{2}+k\pi ,(k\in \mathbb{Z})$; $x=\frac{\pi }{6}+k\pi ,(k\in \mathbb{Z})$.

Bài 5 trang 37 SGK Toán lớp 11 Đại số: Giải các phương trình sau:

a) $\cos x-\sqrt{3}\sin 2x=\sqrt{2}$;

b) 3sin3x − 4cos3x = 5 ;

c) $2sinx+2cosx-\sqrt{2}=0$;

d) 5cos2x + 12sin2x − 13 = 0.

Lời giải:

a) $\cos x-\sqrt{3}\sin 2x=\sqrt{2}$

$\iff \frac{1}{2}\cos x-\frac{\sqrt{3}}{2}\sin x=\frac{\sqrt{2}}{2}$

$\iff \cos x\cos \frac{\pi }{3}-\sin x\sin \frac{\pi }{3}=\frac{\sqrt{2}}{2}$

$\iff \cos \left(x+\frac{\pi }{3}\right)=\cos \frac{\pi }{4}$

$\iff \left[\begin{array}{l}x+\frac{\pi }{3}=\frac{\pi }{4}+k2\pi \\ x+\frac{\pi }{3}=-\frac{\pi }{4}+k2\pi \end{array}\right.$ $\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=-\frac{\pi }{12}+k2\pi \\ x=-\frac{7\pi }{12}+k2\pi \end{array}\right.(k\in \mathbb{Z})$

Vậy nghiệm của phương trình là $x=-\frac{\pi }{12}+k2\pi$; $x=-\frac{7\pi }{12}+k2\pi (k\in \mathbb{Z})$

b) 3sin3x − 4cos3x = 5

$\iff \frac{3}{5}\sin 3x-\frac{4}{5}\cos 3x=1$

Đặt $\left\{\begin{array}{l}\sin \alpha =\frac{3}{5}\\ \cos \alpha =\frac{4}{5}\end{array}\right.$ , phương trình trở thành:

$\sin 3x\sin \alpha –\cos 3x\cos \alpha =1$

$\iff \cos 3x\cos \alpha -\sin 3x\sin \alpha =-1$

$\iff cos(3x+\alpha )=–1$

$\iff 3x+\alpha =\pi +k2\pi$

$\iff 3x=\pi -\alpha +k2\pi$

$\iff x=\frac{\pi -\alpha }{3}+\frac{k2\pi }{3}\text{ (k}\in \mathbb{Z}\text{)}$

Vậy các nghiệm của phương trình là $x=\frac{\pi -\alpha }{3}+\frac{k2\pi }{3}\text{ (k}\in \mathbb{Z}\text{)}$ với ( $\sin \alpha =\frac{3}{5},\cos \alpha =\frac{4}{5}$).

c)  $2sinx+2cosx-\sqrt{2}=0$

$\iff 2sinx+2cosx=\sqrt{2}$

$\iff \frac{2}{2\sqrt{2}}\sin x+\frac{2}{2\sqrt{2}}\cos x=\frac{\sqrt{2}}{2\sqrt{2}}$

$\iff \frac{1}{\sqrt{2}}\sin x+\frac{1}{\sqrt{2}}\cos x=\frac{1}{2}$

$\iff \sin x\sin \frac{\pi }{4}+\cos x\cos \frac{\pi }{4}=\frac{1}{2}$

$\iff \cos \left(x-\frac{\pi }{4}\right)=\cos \frac{\pi }{3}$

$\iff \left[\begin{array}{l}x-\frac{\pi }{4}=\frac{\pi }{3}+k2\pi \\ x-\frac{\pi }{4}=-\frac{\pi }{3}+k2\pi \end{array}\right.$ $\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=\frac{7\pi }{12}+k2\pi \\ x=-\frac{\pi }{12}+k2\pi \end{array}\right.(k\in \mathbb{Z})$

Vậy các nghiệm của phương trình là $x=\frac{7\pi }{12}+k2\pi$  hoặc  $x=-\frac{\pi }{12}+k2\pi ,k\in \mathbb{Z}$.

d) 5cos2x + 12sin2x − 13 = 0

$\iff \frac{5}{13}\cos 2x+\frac{12}{13}\sin 2x=1$

Đặt $\left\{\begin{array}{l}\sin \alpha =\frac{12}{13}\\ \cos \alpha =\frac{5}{13}\end{array}\right.$, khi đó phương trình trở thành:

$cos2xcos\alpha +sin2xsin\alpha =1$

$\iff cos\left(2x–\alpha \right)=1$

$\iff 2x-\alpha =k2\pi$

$\iff x=\frac{\alpha }{2}+k\pi \text{ (k}\in \mathbb{Z}\text{)}$

Vậy nghiệm của phương trình là $x=\frac{\alpha }{2}+k\pi ,(k\in \mathbb{Z})$ với $\sin \alpha =\frac{12}{13};\cos \alpha =\frac{5}{13}$.

Bài 6 trang 37 SGK Toán lớp 11 Đại số: Giải các phương trình sau:

a) tan(2x + 1)tan(3x – 1) = 1;

b) $\tan x+\tan \left(x+\frac{\pi }{4}\right)=1$.

Lời giải:

a) tan(2x + 1)tan(3x – 1) = 1

Điều kiện: $\left\{\begin{array}{l}\cos (2x+1)\ne 0\\ \cos (3x-1)\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}2x+1\ne \frac{\pi }{2}+k\pi \\ 3x-1\ne \frac{\pi }{2}+k\pi \end{array}\right.$

 $\iff \left\{\begin{array}{l}2x\ne \frac{\pi }{2}-1+k\pi \\ 3x\ne \frac{\pi }{2}+1+k\pi \end{array}\right.$

$\iff \left\{\begin{array}{l}x\ne \frac{\pi }{4}-\frac{1}{2}+\frac{k\pi }{2}\\ x\ne \frac{\pi }{6}+\frac{1}{3}+\frac{k\pi }{3}\end{array}\right.\left(k\in \mathbb{Z}\right)$

Ta có: tan(2x + 1)tan(3x – 1) = 1

$\iff \tan (2x+1)=\frac{1}{\tan (3x-1)}$

$\iff \tan (2x+1)=\cot (3x-1)$

$\iff \tan (2x+1)=\tan \left(\frac{\pi }{2}-3x+1\right)$

$\iff 2x+1=\frac{\pi }{2}-3x+1+k\pi$

$\iff 5x=\frac{\pi }{2}+k\pi$

$\iff x=\frac{\pi }{10}+\frac{k\pi }{5},(k\in \mathbb{Z})\left(tm\right)$

Vậy các nghiệm của phương trình là $x=\frac{\pi }{10}+\frac{k\pi }{5}(k\in \mathbb{Z})$.

b) $\tan x+\tan \left(x+\frac{\pi }{4}\right)=1$

Điều kiện: $\left\{\begin{array}{l}\cos x\ne 0\\ \cos \left(x+\frac{\pi }{4}\right)\ne 0\end{array}\right.$ $\iff \left\{\begin{array}{l}x\ne \frac{\pi }{2}+k\pi \\ x+\frac{\pi }{4}\ne \frac{\pi }{2}+k\pi \end{array}\right.$ $\iff \left\{\begin{array}{l}x\ne \frac{\pi }{2}+k\pi \\ x\ne \frac{\pi }{4}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Ta có: $\tan x+\tan \left(x+\frac{\pi }{4}\right)=1$

$\iff \tan x+\frac{\tan x+\tan \frac{\pi }{4}}{1-\tan x\tan \frac{\pi }{4}}=1$

$\iff \tan x+\frac{\tan x+1}{1-\tan x}=1$

$\iff tanx–ta{n}^{2}x+tanx+1=1-tanx$

$\iff ta{n}^{2}x-3tanx=0$

$\iff tanx\left(tanx–3\right)=0$

$\iff \left[\begin{array}{l}\tan x=0\\ \tan x=3\end{array}\right.$

 $\iff \left[\begin{array}{l}x=k\pi \\ x=\arctan 3+k\pi \end{array}\right.(k\in \mathbb{Z})$ (Thỏa mãn)

Vậy nghiệm của phương trình là $x=k\pi$;   $x=\arctan 3+k\pi ,(k\in \mathbb{Z})$

Bài giảng Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (Tiết 1)

Bài giảng Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (Tiết 2)

Xem thêm lời giải bài tập Toán lớp 11 Đại số và Giải tích hay, chi tiết khác:

Ôn tập chương 1

Bài 1: Quy tắc đếm

Bài 2: Hoán vị - chỉnh hợp – tổ hợp

Bài 3: Nhị thức Niu-tơn

Bài 4: Phép thử và biến cố

Xem thêm tài liệu Toán lớp 11 Đại số và Giải tích hay, chi tiết khác:

Lý thuyết Một số phương trình lượng giác thường gặp

Trắc nghiệm Một số phương trình lượng giác thường gặp có đáp án