Toán 11 Bài 2: Dãy số

Với giải bài tập Toán lớp 11 Bài 2: Dãy số chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11.

1 1,259 03/11/2022

Tải về

Trang trước

Trang sau

Mục lục Giải Toán 11 Bài 2: Dãy số

Video giải Toán 11 Bài 2: Dãy số

Hoạt động 1 trang 85 SGK Toán lớp 11 Đại số: Cho hàm số $f (n) = \frac{1}{2 n - 1}, n \in ℕ *$ . Tính f(1), f(2), f(3), f(4), f(5).

Lời giải:

$f (1) = \frac{1}{2.1 - 1} = \frac{1}{2 - 1} = \frac{1}{1} = 1 f (2) = \frac{1}{2.2 - 1} = \frac{1}{4 - 1} = \frac{1}{3} f (3) = \frac{1}{2.3 - 1} = \frac{1}{6 - 1} = \frac{1}{5} f (4) = \frac{1}{2.4 - 1} = \frac{1}{8 - 1} = \frac{1}{7} f (5) = \frac{1}{2.5 - 1} = \frac{1}{10 - 1} = \frac{1}{9}$

Hoạt động 2 trang 86 SGK Toán lớp 11 Đại số: Hãy nêu các phương pháp cho một hàm số và ví dụ minh họa.

Lời giải:

+ Hàm số cho bằng bảng

Ví dụ:

Hãy nêu các phương pháp cho một hàm số (ảnh 1)

+ Hàm số cho bằng công thức

Ví dụ: $y = \frac{2 x + 1}{x}$

Hoạt động 3 trang 86 SGK Toán lớp 11 Đại số: Viết năm số hạng đầu và số hạng tổng quát của các dãy số sau:

a) Dãy nghịch đảo của các số tự nhiên lẻ;

b) Dãy các số tự nhiên chia cho 3 dư 1.

Lời giải:

a) Năm số hạng đầu: $\frac{1}{1}; \frac{1}{3}; \frac{1}{5}; \frac{1}{7}; \frac{1}{9}$

Số hạng tổng quát của dãy số: $\frac{1}{2 n - 1} (n \in ℕ *)$

b) Năm số hạng đầu: 1; 4; 7; 10; 13

Số hạng tổng quát của dãy số: 3n + 1 $(n \in ℕ)$

Hoạt động 4 trang 87 SGK Toán lớp 11 Đại số: Viết mười số hạng đầu của dãy Phi-bô-na-xi.

Lời giải:

Mười số hạng đầu của dãy Phi-bô-na-xi là: 1; 1; 2; 3; 5; 8; 13; 21; 34; 55.

Hoạt động 5 trang 88 SGK Toán lớp 11 Đại số: Cho các dãy số (u_n) và (v_n) với $u_{n} = 1 + \frac{1}{n}; v_{n} = 5 n - 1$ .

a) Tính u_n+1, v_n+1.

b) Chứng minh u_n+1< u_n và v_n+1> v_n, với mọi $n \in ℕ *$ .

Lời giải:

a) $u_{n + 1} = 1 + \frac{1}{n + 1}$

v_n+1 = 5(n + 1) - 1 = 5n + 4

+ Ta có:

$u_{n + 1} - u_{n} = (1 + \frac{1}{n + 1}) - (1 + \frac{1}{n}) = \frac{1}{n + 1} - \frac{1}{n} = \frac{n - (n + 1)}{n (n + 1)} = \frac{- 1}{n (n + 1)} < 0, \forall n \in ℕ^{*}$

Suy ra u_n+1– u_n < 0

Vậy u_n+1< u_n,

+ Lại có: v_n+1– v_n= (5n + 4) – (5n – 1) = 5 > 0

Suy ra v_n+1– v_n> 0

Vậy v_n+1> v_n, $\forall n \in ℕ *$

Hoạt động 6 trang 88 SGK Toán lớp 11 Đại số: Chứng minh các bất đẳng thức

$\frac{n}{n^{2} + 1} \leq \frac{1}{2}$ và $\frac{n^{2} + 1}{2 n} \geq 1, \forall n \in ℕ *$ .

Lời giải:

Ta có:

$\frac{n}{n^{2} + 1} - \frac{1}{2} = \frac{2 n - (n^{2} + 1)}{2 (n^{2} + 1)} = \frac{- n^{2} + 2 n - 1}{2 (n^{2} + 1)} = \frac{- (n^{2} - 2 n + 1)}{2 (n^{2} + 1)} = \frac{- {(n - 1)}^{2}}{2 (n^{2} + 1)} \leq 0; \forall n \in ℕ *$

Vì 2(n² + 1) > 0 và $- {(n - 1)}^{2} \leq 0, \forall n \in ℕ *$

Vậy $\frac{n}{n^{2} + 1} \leq \frac{1}{2}; \forall n \in ℕ *$

Lại có: $\frac{n^{2} + 1}{2 n} - 1 = \frac{n^{2} + 1 - 2 n}{2 n}$

$= \frac{{(n - 1)}^{2}}{2 n} \geq 0; \forall n \in ℕ *$

Vì 2n > 0 và ${(n - 1)}^{2} \geq 0, \forall n \in N^{*}$

Vậy $\frac{n^{2} + 1}{2 n} \geq 1, \forall n \in ℕ *$

Bài tập 1 trang 92 SGK Toán lớp 11 Đại số: Viết năm số hạng đầu của các dãy số hạng tổng quát u_n cho bởi công thức.

a) $u_{n} = \frac{n}{2^{n} - 1}$

b) $u_{n} = \frac{2^{n} - 1}{2^{n} + 1}$

c) $u_{n} = {(1 + \frac{1}{n})}^{n}$

d) $u_{n} = \frac{n}{\sqrt{n^{2} + 1}}$

Lời giải:

a) $u_{n} = \frac{n}{2^{n} - 1}$

$u_{1} = \frac{1}{2^{1} - 1} = 1$ ,

$u_{2} = \frac{2}{2^{2} - 1} = \frac{2}{3}$ ,

$u_{3} = \frac{3}{2^{3} - 1} = \frac{3}{7}$ ,

$u_{4} = \frac{4}{2^{4} - 1} = \frac{4}{15}$ ,

$u_{5} = \frac{5}{2^{5} - 1} = \frac{5}{31}$

Vậy năm số hạng đầu tiên của dãy số là

u₁ = 1, $u_{2} = \frac{2}{3}$ , $u_{3} = \frac{3}{7}$ , $u_{4} = \frac{4}{15}$ , $u_{5} = \frac{5}{31}$ .

b) $u_{n} = \frac{2^{n} - 1}{2^{n} + 1}$

$u_{1} = \frac{2^{1} - 1}{2^{1} + 1} = \frac{1}{3}$ ,

$u_{2} = \frac{2^{2} - 1}{2^{2} + 1} = \frac{3}{5}$ ,

$u_{3} = \frac{2^{3} - 1}{2^{3} + 1} = \frac{7}{9}$ ,

$u_{4} = \frac{2^{4} - 1}{2^{4} + 1} = \frac{15}{17}$ ,

$u_{5} = \frac{2^{5} - 1}{2^{5} + 1} = \frac{31}{33}$

Vậy năm số hạng đầu tiên của dãy số là

$u_{1} = \frac{1}{3}$ , $u_{2} = \frac{3}{5}$ , $u_{3} = \frac{7}{9}$ , $u_{4} = \frac{15}{17}$ , $u_{5} = \frac{31}{33}$ .

c) $u_{n} = {(1 + \frac{1}{n})}^{n}$

$u_{1} = {(1 + \frac{1}{1})}^{1} = 2$

, $u_{2} = {(1 + \frac{1}{2})}^{2} = \frac{9}{4}$ ,

$u_{3} = {(1 + \frac{1}{3})}^{3} = \frac{64}{27}$ ,

$u_{4} = {(1 + \frac{1}{4})}^{4} = \frac{625}{256}$ ,

$u_{5} = {(1 + \frac{1}{5})}^{5} = \frac{7776}{3125}$

Vậy năm số hạng đầu tiên của dãy số là

u₁ = 2, $u_{2} = \frac{9}{4}$ , $u_{3} = \frac{64}{27}$ , $u_{4} = \frac{625}{256}$ , $u_{5} = \frac{7776}{3125}$ .

d) $u_{n} = \frac{n}{\sqrt{n^{2} + 1}}$

$u_{1} = \frac{1}{\sqrt{1^{2} + 1}} = \frac{1}{\sqrt{2}}$ ,

$u_{2} = \frac{2}{\sqrt{2^{2} + 1}} = \frac{2}{\sqrt{5}}$ ,

$u_{3} = \frac{3}{\sqrt{3^{2} + 1}} = \frac{3}{\sqrt{10}}$ ,

$u_{4} = \frac{4}{\sqrt{4^{2} + 1}} = \frac{4}{\sqrt{17}}$ ,

$u_{5} = \frac{5}{\sqrt{5^{2} + 1}} = \frac{5}{\sqrt{26}}$

Vậy năm số hạng đầu tiên của dãy số là

$u_{1} = \frac{1}{\sqrt{2}}$ , $u_{2} = \frac{2}{\sqrt{5}}$ , $u_{3} = \frac{3}{\sqrt{10}}$ , $u_{4} = \frac{4}{\sqrt{17}}$ , $u_{5} = \frac{5}{\sqrt{26}}$ .

Bài tập 2 trang 92 SGK Toán lớp 11 Đại số: Cho dãy số (u_n), biết:

u₁ = – 1, u_n+1= u_n + 3 với $n \geq 1$

a) Viết năm số hạng đầu của dãy số.

b) Chứng minh bằng phương pháp quy nạp: u_n = 3n – 4

Lời giải:

a) u₁ = – 1

u₂ = u₁ + 3 = – 1 + 3 = 2

u₃ = u₂ + 3 = 2 + 3 = 5

u₄ = u₃ + 3 = 5 + 3 = 8

u₅ = u₄ + 3 = 8 + 3 = 11

Vậy năm số hạng đầu tiên của dãy số là: u₁ = – 1, u₂ = 2, u₃ = 5, u₄ = 8, u₅ = 11.

b) Chứng minh u_n = 3n – 4 (*) bằng phương pháp quy nạp:

Do u₁ = – 1 = 3.1 – 4 nên (*) đúng với n = 1

Giả sử (*) đúng với $n = k, k \geq 1$ , tức là chứng minh u_k+1= 3(k + 1) – 4

Thật vậy, từ giả thiết u_n+1= u_n + 3, suy ra:

u_k+1= u_k + 3 = 3k – 4 + 3 = (3k + 3) – 4 = 3(k + 1) – 4

Hay u_k+1= 3(k + 1) – 4

Do đó (*) đúng với n = k + 1

Vậy hệ thức đúng với mọi $n \in ℕ *$ .

Bài tập 3 trang 92 SGK Toán lớp 11 Đại số: Dãy số (u_n) cho biết:

$u_{1} = 3, u_{n + 1} = \sqrt{1 + u_{n}^{2}}, n \geq 1$ .

a) Viết năm số hạng đầu của dãy số.

b) Dự đoán công thức số hạng tổng quát u_n và chứng minh công thức đó bằng phương pháp quy nạp.

Lời giải:

a) Ta có:

$u_{2} = \sqrt{1 + u_{1}^{2}} = \sqrt{1 + 3^{2}} = \sqrt{10} u_{3} = \sqrt{1 + u_{2}^{2}} = \sqrt{1 + {(\sqrt{10})}^{2}} = \sqrt{11} u_{4} = \sqrt{1 + u_{3}^{2}} = \sqrt{1 + {(\sqrt{11})}^{2}} = \sqrt{12} u_{5} = \sqrt{1 + u_{4}^{2}} = \sqrt{1 + {(\sqrt{12})}^{2}} = \sqrt{13}$

Vậy năm số hạng đầu của dãy số là:

u₁ = 3, $u_{2} = \sqrt{10}$ , $u_{3} = \sqrt{11}$ , $u_{4} = \sqrt{12}$ , $u_{5} = \sqrt{13}$

b) Ta có:

$u_{1} = 3 = \sqrt{9} = \sqrt{1 + 8} u_{2} = \sqrt{10} = \sqrt{2 + 8} u_{3} = \sqrt{11} = \sqrt{3 + 8} u_{4} = \sqrt{12} = \sqrt{4 + 8} u_{5} = \sqrt{13} = \sqrt{5 + 8}$

Từ trên ta dự đoán $u_{n} = \sqrt{n + 8}$ , với $n \in ℕ * (1)$

Chứng minh công thức (1) bằng phương pháp quy nạp:

Với n = 1, rõ ràng công thức (1) là đúng.

Giả sử (1) đúng với $n = k \geq 1$ , tức là có $u_{k} = \sqrt{k + 8}$ với $k \geq 1$ , ta cần chứng minh

$u_{k + 1} = \sqrt{(k + 1) + 8}$

Theo công thức dãy số, ta có:

$u_{k + 1} = \sqrt{1 + u_{k}^{2}} = \sqrt{1 + {(\sqrt{k + 8})}^{2}}$

$= \sqrt{1 + k + 8} = \sqrt{(k + 1) + 8}$

Như vậy công thức (1) đúng với n = k + 1.

Vậy công thức (1) được chứng minh.

Bài tập 4 trang 92 SGK Toán lớp 11 Đại số: Xét tính tăng, giảm của các dãy số (u_n), biết:

a) $u_{n} = \frac{1}{n} - 2$

b) $u_{n} = \frac{n - 1}{n + 1}$

c) u_n = (- 1)ⁿ(2ⁿ + 1)

d) $u_{n} = \frac{2 n + 1}{5 n + 2}$

Lời giải:

a) Ta có:

$u_{n + 1} - u_{n} = \frac{1}{n + 1} - 2 - \frac{1}{n} + 2 = \frac{1}{n + 1} - \frac{1}{n} = \frac{- 1}{n (n + 1)} < 0 u_{n + 1} < u_{n}, \forall n \in ℕ *$

Vậy (u_n) là dãy số giảm.

Cách khác:

Với mọi $n \in ℕ *$ ta có:

$u_{n + 1} = \frac{1}{n + 1} - 2 < \frac{1}{n} - 2 < u_{n}$

Do đó (u_n) là dãy số giảm.

b) Xét hiệu

$u_{n + 1} - u_{n} = \frac{n + 1 - 1}{n + 1 + 1} - \frac{n - 1}{n + 1} = \frac{n}{n + 2} - \frac{n - 1}{n + 1} = \frac{n (n + 1) - (n - 1) (n + 2)}{(n + 1) (n + 2)} = \frac{n^{2} + n - (n^{2} - n + 2 n - 2)}{(n + 1) (n + 2)} = \frac{n^{2} + n - (n^{2} + n - 2)}{(n + 1) (n + 2)} = \frac{n^{2} + n - n^{2} - n + 2}{(n + 1) (n + 2)} = \frac{2}{(n + 1) (n + 2)} > 0$

Suy ra $u_{n + 1} > u_{n}, \forall n \in ℕ$

Vậy dãy số đã cho là dãy số tăng.

Cách khác:

Với mọi $n \in ℕ *$ ta có:

$u_{n} = \frac{n - 1}{n + 1} = \frac{n + 1 - 2}{n + 1} = 1 - \frac{2}{n + 1} u_{n + 1} = 1 - \frac{1}{(n + 1) + 1} = 1 - \frac{1}{n + 2}$

Ta có:

$\frac{1}{n + 2} < \frac{2}{n + 1} \Rightarrow - \frac{1}{n + 2} > - \frac{2}{n + 1} \Rightarrow 1 - \frac{1}{n + 2} > 1 - \frac{2}{n + 1}$

Suy ra $u_{n + 1} > u_{n}, \forall n \in ℕ *$

Vậy (u_n) là dãy số tăng.

c) Ta có: u₁ = -3; u₂ = 5; u₃ = - 9

suy ra $u_{1} < u_{2} > u_{3}$

Nên (u_n) là dãy số không tăng, không giảm.

d) Với $n \in ℕ *, u_{n} \neq 0$ ta có:

$\frac{u_{n + 1}}{u_{n}} = \frac{2 n + 3}{5 n + 7} \cdot \frac{5 n + 2}{2 n + 1} = \frac{10 n^{2} + 19 n + 6}{10 n^{2} + 19 n + 7} < 1$

Suy ra $u_{n + 1} < u_{n}, \forall n \in ℕ *$

Vậy (u_n) là dãy số giảm.

Cách khác:

$u_{n + 1} - u_{n} = \frac{2 (n + 1) + 1}{5 (n + 1) + 2} - \frac{2 n + 1}{5 n + 2} = \frac{2 n + 3}{5 n + 7} - \frac{2 n + 1}{5 n + 2} = \frac{(2 n + 3) (5 n + 2) - (2 n + 1) (5 n + 7)}{(5 n + 7) (5 n + 2)} = \frac{(10 n^{2} + 15 n + 4 n + 6) - (10 n^{2} + 5 n + 14 n + 7)}{(5 n + 7) (5 n + 2)} = \frac{- 1}{(5 n + 7) (5 n + 2)} < 0, \forall n \in ℕ *$

Suy ra $u_{n + 1} - u_{n} < 0, \forall n \in ℕ *$

Suy ra $u_{n + 1} < u_{n}, \forall n \in ℕ *$

Vậy (u_n) là dãy số giảm.

Bài tập 5 trang 92 SGK Toán lớp 11 Đại số: Trong các dãy số (u_n) sau, dãy số nào bị chặn dưới, bị chặn trên và bị chặn?

a) u_n = 2n² – 1

b) $u_{n} = \frac{1}{n (n + 2)}$

c) $u_{n} = \frac{1}{2 n^{2} - 1}$

d) u_n = sin n + cos n

Lời giải:

a) Ta có $n \geq 1$ suy ra $n^{2} \geq 1$ suy ra $2 n^{2} \geq 2$

Suy ra $2 n^{2} - 1 \geq 1$

Suy ra $u_{n} \geq 1, \forall n \in ℕ *$

Do đó (u_n) bị chặn dưới bởi 1

Ngoài ra (u_n) không bị chặn trên vì không tồn tại số M nào để $2 n^{2} - 1 < M, \forall n \in ℕ *$ .

b) Dễ thấy $u_{n} > 0, \forall n \in ℕ *$

Mặt khác, vì: $\{\begin{cases} n \geq 1 \Rightarrow n^{2} \geq 1 \\ 2 n \geq 2 \end{cases}$

$\Rightarrow n (n + 2) = n^{2} + 2 n \geq 1 + 2 = 3 \Rightarrow \frac{1}{n (n + 2)} \leq \frac{1}{3} \Rightarrow u_{n} \leq \frac{1}{3}, \forall n \in ℕ *$

$\Rightarrow 0 < u_{n} \leq \frac{1}{3}$ với mọi $n \in ℕ *$ .

Vậy dãy số bị chặn.

c) Dễ thấy $u_{n} = \frac{1}{2 n^{2} - 1} > 0$ với mọi $n \in ℕ *$

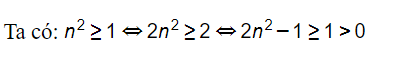
Dãy số nào bị chặn dưới, bị chặn trên và bị chặn (ảnh 1)

Suy ra $0 < \frac{1}{2 n^{2} - 1} \leq 1, \forall n \in ℕ *$

Vậy $0 < u_{n} \leq 1, \forall n \in ℕ *$ tức dãy số bị chặn.

d) Ta có:

$\sin n + \cos n = \sqrt{2} (\frac{1}{\sqrt{2}} \sin n + \frac{1}{\sqrt{2}} \cos n) = \sqrt{2} (\sin n \cos \frac{π}{4} + \cos n \sin \frac{π}{4}) = \sqrt{2} \sin (n + \frac{π}{4})$

Vì $- 1 \leq \sin (n + \frac{π}{4}) \leq 1$

Suy ra $- \sqrt{2} \leq \sqrt{2} \sin (n + \frac{π}{4}) \leq \sqrt{2}$

Suy ra $- \sqrt{2} \leq \sin n + \cos n \leq \sqrt{2}, \forall n \in ℕ *$

Vậy $- \sqrt{2} \leq u_{n} \leq \sqrt{2} \forall n \in ℕ *$ , tức là dãy số là dãy số bị chặn.

Bài giảng Toán 11 Bài 2: Dãy số

Xem thêm lời giải bài tập Toán lớp 11 hay, chi tiết khác:

Bài 3: Cấp số cộng

Bài 4: Cấp số nhân

Ôn tập chương 3

Bài 1: Phép biến hình

Bài 2: Phép tịnh tiến

Xem thêm tài liệu Toán lớp 11 hay, chi tiết khác:

Lý thuyết Dãy số

Trắc nghiệm Dãy số có đáp án

1 1,259 03/11/2022

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3