Chứng minh rằng (11^10) – 1 chia hết cho 100
Với giải Bài tập 6 trang 58 SGK Toán lớp 11 Đại số và Giải tích được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:
Giải Toán 11 Bài 3: Nhị thức Niu - tơn
Video Bài tập 6 trang 58 SGK Toán lớp 11 Đại số
Bài tập 6 trang 58 SGK Toán lớp 11 Đại số: Chứng minh rằng:
a) 1110 – 1 chia hết cho 100;
b) 101100 – 1 chia hết cho 10 000;
c) là một số nguyên.
Lời giải:
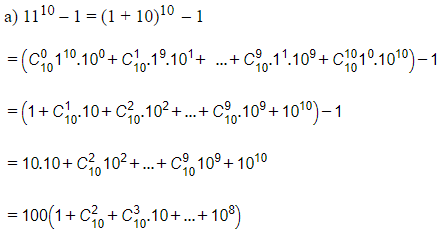
Tổng sau cùng là tích của 100 với một tổng nên nó chia hết cho 100 suy ra 1110 – 1 chia hết cho 100 .
Vậy 1110 – 1 chia hết cho 100.
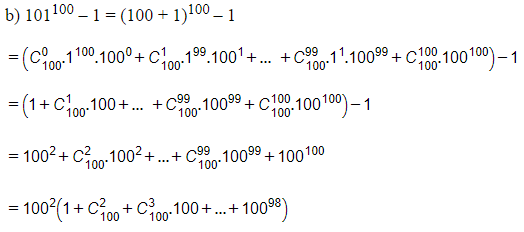
Tổng sau cùng chia hết cho 1002 = 10 000 nên 101100 – 1 chia hết cho 10 000.
c) Ta có:
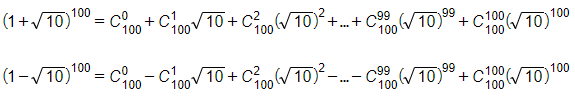
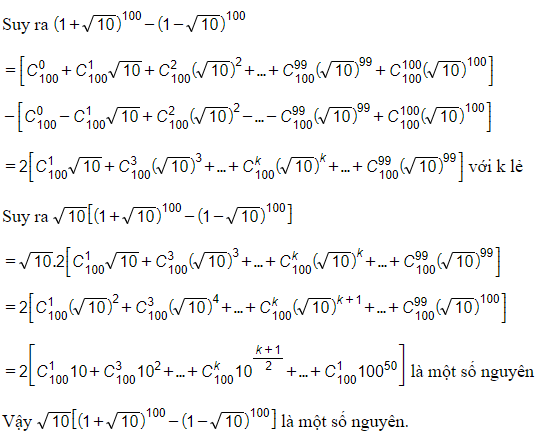
Xem thêm lời giải bài tập Toán lớp 11 hay, chi tiết khác:
Hoạt động 2 trang 57 SGK Toán lớp 11 Đại số: Dùng tam giác Pa-xcan, chứng tỏ rằng...
Bài tập 1 trang 57 SGK Toán lớp 11 Đại số: Viết khai triển theo công thức nhị thức Niu-tơn...
Bài tập 2 trang 58 SGK Toán lớp 11 Đại số: Tìm hệ số của x3trong khai triển của biểu thức...
Bài tập 3 trang 58 SGK Toán lớp 11 Đại số: Biết hệ số của x2trong khai triển của (1 – 3x)nlà 90. Tìm n...
Bài tập 4 trang 58 SGK Toán lớp 11 Đại số: Tìm số hạng không chứa x trong khai triển của ...
Bài tập 5 trang 58 SGK Toán lớp 11 Đại số: Từ khai triển của biểu thức (3x – 4)17 thành đa thức...
Xem thêm các chương trình khác:
- Giải sgk Hóa học 11 | Giải bài tập Hóa học 11 Học kì 1, Học kì 2 (Sách mới)
- Lý thuyết Hóa học 11(sách mới) | Kiến thức trọng tâm Hóa 11
- Giải sbt Hóa học 11 (sách mới) | Sách bài tập Hóa học 11
- Các dạng bài tập Hóa học lớp 11
- Giáo án Hóa học lớp 11 mới nhất
- Tóm tắt tác phẩm Ngữ văn 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 11 (hay nhất) | Để học tốt Ngữ Văn 11 (sách mới)
- Soạn văn 11 (ngắn nhất) | Để học tốt Ngữ văn 11 (sách mới)
- Tác giả tác phẩm Ngữ văn 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Văn mẫu 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 11 (thí điểm)
- Giải sgk Tiếng Anh 11 | Giải bài tập Tiếng anh 11 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 11 (sách mới) | Sách bài tập Tiếng Anh 11
- Giải sbt Tiếng Anh 11 (thí điểm)
- Giải sgk Lịch sử 11 | Giải bài tập Lịch sử 11 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch Sử 11(sách mới) | Kiến thức trọng tâm Lịch Sử 11
- Giải Tập bản đồ Lịch sử 11
- Giải sgk Vật Lí 11 | Giải bài tập Vật lí 11 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Vật Lí 11 (sách mới) | Sách bài tập Vật Lí 11
- Lý thuyết Vật Lí 11 (sách mới) | Kiến thức trọng tâm Vật Lí 11
- Các dạng bài tập Vật Lí lớp 11
- Giáo án Vật lí lớp 11 mới nhất
- Giải sgk Sinh học 11 | Giải bài tập Sinh học 11 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Sinh học 11 (sách mới) | Kiến thức trọng tâm Sinh 11
- Giải sgk Giáo dục công dân 11
- Lý thuyết Giáo dục công dân 11
- Lý thuyết Địa Lí 11 (sách mới) | Kiến thức trọng tâm Địa lí 11
- Giải Tập bản đồ Địa Lí 11
- Giải sgk Giáo dục quốc phòng - an ninh 11
