Đáp án đúng: D

*Lời giải:

$\sin \left(\frac{2x}{3}-\frac{\pi }{3}\right)=0$
$\iff \frac{2x}{3}-\frac{\pi }{3}=k\pi$
$\iff \frac{2x}{3}=\frac{\pi }{3}+k\pi$
$\iff x=\frac{\pi }{2}+\frac{3}{2}k\pi$

*Phương pháp giải:

- Biến đổi và giải phương trình tìm ra nghiệm x 

*Một số lý thuyết và dạng bài tập về hàm số lượng giác:

1. Định nghĩa hàm số lượng giác

- Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là $\mathbb{R}$.

- Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là $\mathbb{R}$.

- Hàm số cho bằng công thức $y=\frac{\sin \alpha }{\cos \alpha }$được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $\mathbb{R}\mathrm{\setminus }\left\{\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right\}$.

- Hàm số cho bằng công thức $y=\frac{\cos \alpha }{\sin \alpha }$được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $\mathbb{R}\mathrm{\setminus }\left\{k\pi |k\in \mathbb{Z}\right\}$.

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a, Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) có tập xác định là D.

+) Hàm số f(x) được gọi là hàm số chẵn nếu $\mathrm{\forall }x\in D$thì $-x\in D$và $f(-x)=f(x)$. Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.

+) Hàm số f(x) được gọi là hàm số lẻ nếu $\mathrm{\forall }x\in D$thì $-x\in D$và $f(-x)=-f(x)$. Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

b, Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T $\ne$0 sao cho với mọi $x\in D$ta có:

+) $x+T\in D$và $x-T\in D$

+) $f(x+T)=f(x)$

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Nhận xét:

Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2$\pi$.

Các hàm số y = tanx, y=cotx tuần hoàn chu kì $\pi$.

3. Đồ thị và tính chất của hàm số y = sinx

- Tập xác định là $\mathbb{R}$.

- Tập giá trị là [-1;1].

- Là hàm số lẻ và tuần hoàn chu kì 2$\pi$.

- Đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k2\pi ;\frac{\pi }{2}+k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left(\frac{\pi }{2}+k2\pi ;\frac{3\pi }{2}+k2\pi \right)$.

- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

4. Đồ thị và tính chất của hàm số y = cosx

Tập xác định là $\mathbb{R}$.

Tập giá trị là [-1;1].

Là hàm số chẵn và tuần hoàn chu kì 2$\pi$.

Đồng biến trên mỗi khoảng $\left(-\pi +k2\pi ;k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left(k2\pi ;\pi +k2\pi \right)$.

Có đồ thị là một đường hình sin đối xứng qua trục tung.

5. Đồ thị và tính chất của hàm số y = tanx

Tập xác định là $\mathbb{R}\mathrm{\setminus }\left\{\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right\}$.

Tập giá trị là $\mathbb{R}$.

Là hàm số lẻ và tuần hoàn chu kì $\pi$.

Đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi \right)$, $k\in \mathbb{Z}$.

Có đồ thị đối xứng qua gốc tọa độ.

6. Đồ thị và tính chất của hàm số y = cotx

Tập xác định là $\mathbb{R}\mathrm{\setminus }\left\{k\pi |k\in \mathbb{Z}\right\}$.

Tập giá trị là $\mathbb{R}$.

Là hàm số lẻ và tuần hoàn chu kì $\pi$.

Đồng biến trên mỗi khoảng $\left(k\pi ;\pi +k\pi \right)$, $k\in \mathbb{Z}$.

Có đồ thị đối xứng qua gốc tọa độ.

Xem thêm các bài viết liên quan hay, chi tiết

Lý thuyết Hàm số lượng giác – Toán 11 Kết nối tri thức

Toán 11 Bài 3 giải vở bài tập (Kết nối tri thức): Hàm số lượng giác

50 bài tập về Tìm tập xác định, tập giá trị của hàm số lượng giác (có đáp án 2024) và cách giải 

$\mathrm{s}\text{inx}=\frac{1}{2}\iff \mathrm{s}\text{inx}=\sin \frac{\pi }{6}$

$\iff \left[\begin{array}{l}x=\frac{\pi }{6}+k2\pi \\ x=\pi -\frac{\pi }{6}+k2\pi \end{array}\right.$$\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=\frac{\pi }{6}+k2\pi \\ x=\frac{5\pi }{6}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy tập nghiệm của phương trình $S=\left\{\frac{\pi }{6}+k2\pi ;\frac{5\pi }{6}+k2\pi \left|k\in \mathbb{Z}\right.\right\}$.

Chọn D

Ta có: $\mathrm{s}\text{inx}=\frac{1}{2}$

$\mathrm{s}\text{inx}=\frac{1}{2}\iff \mathrm{s}\text{inx}=\sin \frac{\pi }{6}$

$\iff \left[\begin{array}{l}x=\frac{\pi }{6}+k2\pi \\ x=\pi -\frac{\pi }{6}+k2\pi \end{array}\right.(k\in \mathrm{\mathbb{Z}})$

$\iff \left[\begin{array}{l}x=\frac{\pi }{6}+k2\pi \\ x=\frac{5\pi }{6}+k2\pi \end{array}\right.(k\in \mathrm{\mathbb{Z}})$

Chọn B

$\sin \left(x+\frac{\pi }{4}\right)=1$

$\iff x+\frac{\pi }{4}=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$

$\iff x=\frac{\pi }{4}+k2\pi \left(k\in \mathbb{Z}\right)$

Vì $\pi \le x\le 5\pi$ nên $\pi \le \frac{\pi }{4}+k2\pi \le 5\pi$

$\Rightarrow 1\le \frac{1}{4}+2k\le 5$

$\iff \frac{3}{4}\le 2k\le \frac{19}{4}$

$\iff \frac{3}{8}\le k\le \frac{19}{8}$

Mà $k\in \mathbb{Z}$ nên $k\in \left\{1;2\right\}.$

Vậy phương trình có hai nghiệm nằm trong đoạn $\left[\pi ;5\pi \right]$.

Chọn C

Chọn đáp án D

$2\cos 2x+1=0$

$\iff \cos 2x=-\frac{1}{2}$

$\iff 2x=\pm \frac{2\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right)$

$\iff x=\pm \frac{\pi }{3}+k\pi \left(k\in \mathbb{Z}\right)$

Vậy nghiệm của phương trình là $x=\pm \frac{\pi }{3}+k\pi \left(k\in \mathbb{Z}\right)$.

Ta được nghiệm $x = \frac{23\pi }{12}$

+ Tương tự , từ (2) ta có:

  $$\begin{gathered} 0 \le \frac{ - 7\pi }{12}+\hspace{0.17em}k2\pi \le 2\pi \iff 0 \le \frac{ - 7}{12}+\hspace{0.17em}2k\le 2 \\ \iff \frac{7}{24}\le k\le \frac{31}{24} \end{gathered}$$

Mà k nguyên nên k = 1 khi đó $x = \frac{17\pi }{12}$

Vậy có 2 nghiệm thỏa mãn đầu bài 

chọn B. 

Ta có: $\tan ( x + \frac{\pi }{5}) + \sqrt{3} = 0$

$$\begin{gathered} \iff \tan ( x + \frac{\pi }{5}) = - \sqrt{3} \\ \iff x +\hspace{0.17em}\frac{\pi }{5} = -\frac{\pi }{3}+\hspace{0.17em}k\pi \\ \iff x = \frac{- 8\pi }{15}+\hspace{0.17em}k\pi ; k\in Z \end{gathered}$$

chọn B

Điều kiện: $\left\{\begin{array}{l}x\ne \frac{\pi }{2}+\hspace{0.17em}k\pi \\ \frac{x}{2}\ne \frac{\pi }{2}+\hspace{0.17em}k\pi \end{array}\right., k\in \mathrm{\mathbb{Z}}\iff \left\{\begin{array}{l}x\ne \frac{\pi }{2}+\hspace{0.17em}k\pi \\ x\ne \pi +\hspace{0.17em}k2\pi \end{array}\right.$, $k\in \mathrm{\mathbb{Z}}$

Xét phương trình: $\text{tanx}=\tan \frac{x}{2}$

$\iff x=\frac{x}{2}+k\pi ,k\in \mathbb{Z}$

$\iff x=k2\pi ,k\in \mathbb{Z}$ (thỏa mãn điều kiện)

Vậy nghiệm của phương trình là: $x=k2\pi ,k\in \mathbb{Z}$.

Chọn A

tan(2x - 15°) = 1

Điều kiện: $\text{cos}\left(2x-{15}^0\right)\ne 0$

$\iff$tan(2x - 15°) = 1

$\iff$2x – 15⁰ = 45⁰ + k.180⁰

$\iff$x = 60⁰ + k.90⁰

Vì – 90⁰ < x < 90⁰ nên x = - 60⁰ hoặc x = 40⁰.

Vậy x = - 60⁰ và x = 30⁰.

Chọn D

Điều kiện: $\text{cos}x\ne 0$

$\tan x=\tan \frac{3\pi }{11}$

$\iff x=\frac{3\pi }{11}+k\pi ,k\in \mathbb{Z}$

Mà $\frac{\pi }{4}<\frac{3\pi }{11}+k\pi <2\pi$

$\Rightarrow -\frac{1}{44}<k<\frac{19}{11}$

Mà $k\in \mathbb{Z}$ nên $k\in \left\{0;1\right\}$

Vậy phương trình đã cho có hai nghiệm.

Chọn B

Đáp án đúng là B

Lời giải

Điều kiện xác định: $x\ne k\pi , k\in \mathbb{Z}.$

$3\cot x-\sqrt{3}=0$

$\iff \cot x=\frac{\sqrt{3}}{3}$

$\iff \cot x=\cot \left(\frac{\pi }{3}\right)$

$\iff x=\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}.$ (thỏa mãn điều kiện)

Vậy nghiệm của phương trình là: $x=\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}$.

*Phương pháp giải:

Nắm được bảng giá trị lượng giác các góc đặc biệt

*Lý thuyết:

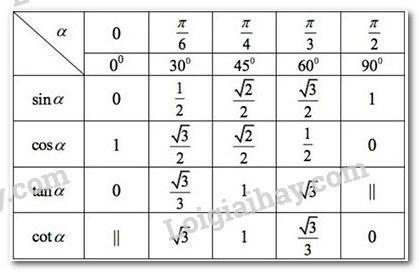
b, Giá trị lượng giác của các góc có liên quan đặc biệt (cos đối, sin bù, phụ chéo, khác pi tan)

• Góc đối nhau ($\alpha$ và - $\alpha$)

$\begin{array}{l}\sin \left(-\alpha \right)=-\sin \alpha \\ \cos \left(-\alpha \right)=\cos \alpha \\ \tan \left(-\alpha \right)=-\tan \alpha \\ \cot \left(-\alpha \right)=-\cot \alpha \end{array}$

• Góc bù nhau ($\alpha$ và $\pi$ - $\alpha$)

$\begin{array}{l}\sin \left(\pi -\alpha \right)=\sin \alpha \\ \cos \left(\pi -\alpha \right)=-\cos \alpha \\ \tan \left(\pi -\alpha \right)=-\tan \alpha \\ \cot \left(\pi -\alpha \right)=-\cot \alpha \end{array}$

• Góc phụ nhau ($\alpha$ và $\frac{\pi }{2}$ - $\alpha$)

$\begin{array}{l}\sin \left(\frac{\pi }{2}-\alpha \right)=c\mathrm{o}\mathrm{s}\alpha \\ \cos \left(\frac{\pi }{2}-\alpha \right)=\sin \alpha \\ \tan \left(\frac{\pi }{2}-\alpha \right)=\cot \alpha \\ \cot \left(\frac{\pi }{2}-\alpha \right)=\tan \alpha \end{array}$

• Góc hơn kém $\pi$ ($\alpha$ và $\pi$ + $\alpha$)

$\begin{array}{l}\sin \left(\pi +\alpha \right)=-\sin \alpha \\ \cos \left(\pi +\alpha \right)=-\cos \alpha \\ \tan \left(\pi +\alpha \right)=\tan \alpha \\ \cot \left(\pi +\alpha \right)=\cot \alpha \end{array}$

Xem thêm

Lý thuyết Giá trị lượng giác của góc lượng giác – Toán 11 Kết nối tri thức 

Đáp án đúng là B

Lời giải

Điều kiện xác định: $x\ne k\pi ,k\in \mathbb{Z}$

$2\cot x-\sqrt{3}=0$

$\iff 2\cot x=\sqrt{3}$

$\iff \cot x=\frac{\sqrt{3}}{2}$

$\iff x=\mathrm{arccot}\left(\frac{\sqrt{3}}{2}\right)+k\pi \left(k\in \mathbb{Z}\right)$ (thỏa mãn điều kiện).

Vậy nghiệm của phương trình là: $x=\mathrm{arccot}\left(\frac{\sqrt{3}}{2}\right)+k\pi \left(k\in \mathbb{Z}\right)$.

*Phương pháp giải:

Đưa về dạng cosx=a

Phương trình cosx = a

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $\left|\text{cosx }\right|\le 1$ với mọi x.

- Trường hợp $\left|\text{\hspace{0.17em}a }\right|\le 1$.

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x=\pm \alpha +k2\pi ;k\in \mathbb{Z}$

- Chú ý:

a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là: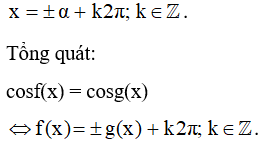 

b) Phương trình cos x= cosβ⁰ có các nghiệm là $x=\pm {\beta }^0+\text{\hspace{0.17em}}k{360}^0;k\in \mathbb{Z}$

c) Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}0\le \alpha \le \pi \\ \cos \alpha =a\end{array}\right.$ thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là:

$x=\pm \arccos a\text{\hspace{0.17em}}+k2\pi ;k\in \mathbb{Z}$

*Lý thuyết

1. Phương trình sinx = a.

Xét phương trình sinx = a (1)

- Trường hợp |a| > 1

Phương trình (1) vô nghiệm vì |sinx| ≤ 1 với mọi x.

- Trường hợp |a| ≤ 1

Gọi α là số đo bằng radian của một cung lượng giác. Khi đó, phương trình sinx = a có các nghiệm là:

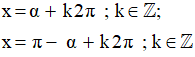
Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}\frac{-\pi }{2}\le \alpha \le \frac{\pi }{2}\\ \sin \alpha =a\end{array}\right.$ thì ta viết α = arcsina (đọc là ac-sin-a; nghĩa là cung có sin bằng a). Khi đó, các nghiệm của phương trình sinx = a được viết là:

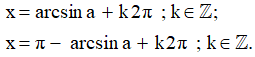
- Chú ý:

a) Phương trình sinx = sinα; với α là một số cho trước, có các nghiệm là:

$x=\alpha +\text{\hspace{0.17em}\hspace{0.17em}}k2\pi$ và $x=\pi -\alpha +\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$

Tổng quát: 

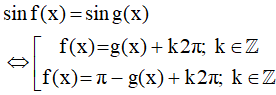
b) Phương trình sinx = sinβ⁰ có các nghiệm là:

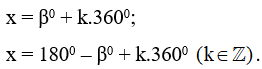
c) Trong một công thức về nghiệm của phương trình lương giác không được dùng đồng thời hai đơn vị độ và radian.

d) Các trường hợp đặc biệt:

+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là $x=\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$.

+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là $x=-\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k2\pi ;k\in \mathbb{Z}$.

+ Khi a = 0:  Phương trình sinx = 0 có các nghiệm là $x=k\pi ;k\in \mathbb{Z}$.

2.. Phương trình cosx = a

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $\left|\text{cosx }\right|\le 1$ với mọi x.

- Trường hợp $\left|\text{\hspace{0.17em}a }\right|\le 1$.

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x=\pm \alpha +k2\pi ;k\in \mathbb{Z}$

- Chú ý:

a) Phương trình cosx = cosα, với α là một số cho trước, có các nghiệm là: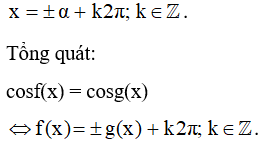 

b) Phương trình cos x= cosβ⁰ có các nghiệm là $x=\pm {\beta }^0+\text{\hspace{0.17em}}k{360}^0;k\in \mathbb{Z}$

c) Nếu số thực α thỏa mãn điều kiện: $\left\{\begin{array}{c}0\le \alpha \le \pi \\ \cos \alpha =a\end{array}\right.$ thì ta viết α = arccosa (đọc là ac – cosin- a, có nghĩa là cung có cosin bằng a). Khi đó, các nghiệm của phương trình cos x = a còn được viết là:

$x=\pm \arccos a\text{\hspace{0.17em}}+k2\pi ;k\in \mathbb{Z}$

d) Các trường hợp đặc biệt:

+ Khi a = 1; phương trình cosx = 1 có các nghiệm là: $x=k2\pi ;k\in \mathbb{Z}$.

+ Khi a = – 1; phương trình cosx = – 1 có các nghiệm là: $x=\pi +k2\pi ;k\in \mathbb{Z}$

+ Khi a = 0; phương trình cosx = 0 có các nghiệm là: $x=\frac{\pi }{2}+\text{\hspace{0.17em}\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$.

3. Phương trình tanx = a.

- Điều kiện xác định của phương trình là $x\ne \frac{\pi }{2}+k\pi ;k\in \mathbb{Z}$.

Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là: $x=\arctan a+\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$

- Chú ý:

a) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là:

$x=\alpha +\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$

Tổng quát; tan f(x) = tan g(x) $\Rightarrow f\left(x\right)\text{\hspace{0.17em}\hspace{0.17em}}=g\left(x\right)+\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$.

b) Phương trình tanx = tanβ⁰ có các nghiệm là: $x={\beta }^0+k{.180}^0;k\in \mathbb{Z}$.

4. Phương trình cotx = a

Điều kiện xác định của phương trình $$$x\ne k\pi ;k\in \mathbb{Z}$.

Kí hiệu x = arccota (đọc là ac– côtang – a; nghĩa là cung có côtang bằng a). Khi đó, nghiệm của phương trình cotx = a là: $x=\mathrm{arccot}a+\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$

- Chú ý:

a) Phương trình cotx = cotα, với α là một số cho trước, có các nghiệm là:

$x=\alpha +\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$

Tổng quát; cot f(x) = cot g(x) $\Rightarrow f\left(x\right)\text{\hspace{0.17em}\hspace{0.17em}}=g\left(x\right)+\text{\hspace{0.17em}}k\pi ;k\in \mathbb{Z}$.

b) Phương trình cot x = cot β⁰ có các nghiệm là: $x={\beta }^0+k{.180}^0;k\in \mathbb{Z}$

Xem thêm

Lý thuyết Phương trình lượng giác cơ bản (mới  + Bài Tập) – Toán 11 

Đáp án đúng: C

* Lời giải:

* Phương pháp giải:

- Biến đổi và giải phương trình tìm ra nghiệm x 

*Một số lý thuyết và dạng bài tập về hàm số lượng giác:

1. Định nghĩa hàm số lượng giác

- Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là $R$.

- Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là $R$.

- Hàm số cho bằng công thức $y=\frac{\sin \alpha }{\cos \alpha }$được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $R\setminus \left\{\frac{\pi }{2}+k\pi |k\in Z\right\}$.

- Hàm số cho bằng công thức $y=\frac{\cos \alpha }{\sin \alpha }$được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $R\setminus \left\{k\pi |k\in Z\right\}$.

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a, Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) có tập xác định là D.

+) Hàm số f(x) được gọi là hàm số chẵn nếu $\forall x\in D$thì $-x\in D$và $f(-x)=f\left(x\right)$. Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.

+) Hàm số f(x) được gọi là hàm số lẻ nếu $\forall x\in D$thì $-x\in D$và $f(-x)=-f\left(x\right)$. Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

b, Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T $\ne$0 sao cho với mọi $x\in D$ta có:

+) $x+T\in D$và $x-T\in D$

+) $f(x+T)=f\left(x\right)$

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Nhận xét:

Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2$\pi$.

Các hàm số y = tanx, y=cotx tuần hoàn chu kì $\pi$.

3. Đồ thị và tính chất của hàm số y = sinx

- Tập xác định là $R$.

- Tập giá trị là [-1;1].

- Là hàm số lẻ và tuần hoàn chu kì 2$\pi$.

- Đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k2\pi ;\frac{\pi }{2}+k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left(\frac{\pi }{2}+k2\pi ;\frac{3\pi }{2}+k2\pi \right)$.

- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

4. Đồ thị và tính chất của hàm số y = cosx

Tập xác định là $R$.

Tập giá trị là [-1;1].

Là hàm số chẵn và tuần hoàn chu kì 2$\pi$.

Đồng biến trên mỗi khoảng $\left(-\pi +k2\pi ;k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left(k2\pi ;\pi +k2\pi \right)$.

Có đồ thị là một đường hình sin đối xứng qua trục tung.

5. Đồ thị và tính chất của hàm số y = tanx

Tập xác định là $R\setminus \left\{\frac{\pi }{2}+k\pi |k\in Z\right\}$.

Tập giá trị là $R$.

Là hàm số lẻ và tuần hoàn chu kì $\pi$.

Đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi \right)$, $k\in Z$.

Có đồ thị đối xứng qua gốc tọa độ.

6. Đồ thị và tính chất của hàm số y = cotx

Tập xác định là $R\setminus \left\{k\pi |k\in Z\right\}$.

Tập giá trị là $R$.

Là hàm số lẻ và tuần hoàn chu kì $\pi$.

Đồng biến trên mỗi khoảng $\left(k\pi ;\pi +k\pi \right)$, $k\in Z$.

Có đồ thị đối xứng qua gốc tọa độ.

Xem thêm các bài viết liên quan hay, chi tiết

Lý thuyết Hàm số lượng giác – Toán 11 Kết nối tri thức

Toán 11 Bài 3 giải vở bài tập (Kết nối tri thức): Hàm số lượng giác

50 bài tập về Tìm tập xác định, tập giá trị của hàm số lượng giác (có đáp án 2024) và cách giải 

Đáp án đúng: D

*Phương pháp giải:

- tìm điều kiện xác định cho tan và cot để xác định trước

- Thực hiện phép tính chuyển hết về tan hoặc cot để tìm nghiệm

*Lời giải:

Điều kiện: $\left\{\begin{array}{l}\cos 3x\ne 0\\ \sin 2x\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x\ne \frac{\pi }{6}+k\frac{\pi }{3}\\ x\ne \frac{k\pi }{2}\end{array}\right.,k\in \mathbb{Z}$

Xét phương trình: tan3x.cot2x = 1

$\iff \tan 3x=\frac{1}{\cot 2x}$

$\iff \tan 3x=\tan 2x$

$\iff 3x=2x+k\pi ,k\in \mathbb{Z}$

$\iff x=k\pi ,k\in \mathbb{Z}$ (loại do $x\ne \frac{k\pi }{2},k\in \mathbb{Z}$). 

Vậy phương trình vô nghiệm 

* Lý thuyết và các dạng bài cần nắm thêm về hàm số lượng giác:

a. Hàm số y = sinx

- Tập xác định: D = R

- Tập giá trị: [-1;1]

b. Hàm số y = cosx

- Tập xác định: D = R

- Tập giá trị: [-1;1]

c. Hàm số y = tanx

- Tập xác định: $D=R\backslash \left\{\frac{\pi }{2}+k\pi ,k\in Z\right\}$

- Tập giá trị: R

d. Hàm số y = cotx

- Tập xác định: $D=R\backslash \left\{k\pi ,k\in Z\right\}$

- Tập giá trị: R

Dạng 1. Tìm tập xác định của hàm số lượng giác

- Phương pháp giải:

$y=\frac{f\left(x\right)}{g\left(x\right)}$ xác định khi $g\left(x\right)\ne 0$

$y=\sqrt{f\left(x\right)}$ xác định khi $f\left(x\right)\ge 0$

$y=\frac{f\left(x\right)}{\sqrt{g\left(x\right)}}$ xác định khi g(x) > 0

y = tan[u(x)] xác định khi $u\left(x\right)\ne \frac{\pi }{2}+k\pi ,k\in Z$

y = cot[u(x)] xác định khi $u\left(x\right)\ne k\pi ,k\in Z$

$\sin x\ne 0$ khi $x\ne k\pi \left(k\in Z\right)$

$\cos x\ne 0$ khi $x\ne \frac{\pi }{2}+k\pi \left(k\in Z\right)$

$Dạng\; 2.\; Tìm\; tập\; giá\; trị\; của\; hàm\; số\; lượng\; giác$

- Phương pháp giải:

Sử dụng tính bị chặn của hàm số lượng giác

$-1\le \sin \left[u\left(x\right)\right]\le 1;0\le {\sin }^2\left[u\left(x\right)\right]\le 1;$$0\le \left|\sin \left[u\left(x\right)\right]\right|\le 1$

$-1\le \cos \left[u\left(x\right)\right]\le 1;0\le {\cos }^2\left[u\left(x\right)\right]\le 1;$ $0\le \left|\cos \left[u\left(x\right)\right]\right|\le 1$

$\mathrm{Dạng\; 3.\; Tìm\; m\; để\; hàm\; số\; lượng\; giác\; có\; tập\; xác\; định\; là\; R}$

- Phương pháp giải:

$\begin{array}{c}m\ge f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m\ge \underset{x\in \left[a;b\right]}{\max }f\left(x\right)\\ m>f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m>\underset{x\in \left[a;b\right]}{\max }f\left(x\right)\\ m\le f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m\le \underset{x\in \left[a;b\right]}{\min }f\left(x\right)\\ m<f\left(x\right)\forall x\in \left[a;b\right]\Rightarrow m<\underset{x\in \left[a;b\right]}{\min }f\left(x\right)\end{array}$

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Hàm số lượng giác – Toán 11 Kết nối tri thức 

Toán 11 Bài 3 (Kết nối tri thức): Hàm số lượng giác

Bài tập Hàm số lượng giác Toán 11 mới nhất 

Đáp án đúng A

Điều kiện: $\cos 2x \ne 0 \iff 2x\ne \frac{\pi }{2}+\hspace{0.17em}k\pi \iff x\ne \frac{\pi }{4}+\hspace{0.17em}\frac{k\pi }{2}$

Do đó. phương trình đã cho có 2  nghiệm thuộc khoảng$(0; \pi ) là\hspace{0.17em}\frac{\pi }{4}; \frac{3\pi }{4}$

chọn A.