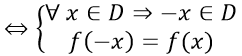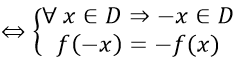Trắc nghiệm Hàm số lượng giác có đáp án (Nhận biết)
-
511 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
18/07/2024Hàm số y=sinx xác định trên:
Xem đáp án
Hàm y=sinx có TXĐ: D = R
Đáp án cần chọn là: D
Câu 2:
17/07/2024Hàm số y = cosx xác định trên:
Xem đáp án
Hàm y = cosx có TXĐ: D = R
Đáp án cần chọn là: D
Câu 3:
17/07/2024Tập xác định của hàm số y = 2sinx là
Xem đáp án
Hàm số y=2sinx xác định trên R nên tập xác định D=R
Đáp án cần chọn là: C
Câu 4:
17/07/2024Tập giá trị của hàm số y=sinx là:
Xem đáp án
Với mọi x ta có:
Do đó, hàm số y = sinx có tập giá trị [−1;1].
Đáp án cần chọn là: B
Câu 5:
17/07/2024Hàm số nào sau đây có tập giá trị là R?
Xem đáp án
Trong các đáp án đã cho chỉ có hàm số y = tan2x có tập giá trị là R, các hàm còn lại đều có tập giá trị là [−1;1].
Đáp án cần chọn là: A
Câu 6:
23/07/2024Hàm số y = cosx nghịch biến trên mỗi khoảng:
Xem đáp án
Hàm số y=cosx nghịch biến trên mỗi khoảng (k2π;π+k2π)
Đáp án cần chọn là: C
Câu 8:
20/07/2024Đồ thị hàm số y = tanx đi qua điểm nào dưới đây?
Xem đáp án
Nếu x=0 thì y=tan0=0 nên điểm O nằm trên đồ thị hàm số y=tanx
Đáp án cần chọn là: A
Câu 11:
21/11/2024Hàm số nào dưới đây là hàm số chẵn?
Xem đáp án
Đáp án đúng là D
*Lời giải
*Phương pháp giải
Sử dụng định nghĩa
Hàm số y = f(x) xác định trên D
+ Hàm số chẵn 
+ Hàm số lẻ 
Chú ý: Một hàm số có thể không chẵn cũng không lẻ
Đồ thị hàm số chẵn nhận trục Oy làm trục đối xứng
Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng
* Quy trình xét hàm số chẵn, lẻ.
B1: Tìm tập xác định của hàm số.
B2: Kiểm tra
Nếu ∀ x ∈ D ⇒ -x ∈ D Chuyển qua bước ba
Nếu ∃ x0 ∈ D ⇒ -x0 ∉ D kết luận hàm không chẵn cũng không lẻ.
B3: xác định f(-x) và so sánh với f(x).
Nếu bằng nhau thì kết luận hàm số là chẵn
Nếu đối nhau thì kết luận hàm số là lẻ
Nếu tồn tại một giá trị ∃ x0 ∈ D mà f(-x0 ) ≠ ± f(x0) kết luận hàm số không chẵn cũng không lẻ.
*Lý thuyết cần nắm và dạng bài về tính chẵn-lẻ của hàm số lượng giác:
a) Tính chẵn, lẻ của hàm số:
* Định nghĩa:
- Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu: thì và f(-x) = f(x).
Đồ thị hàm số chẵn nhận trục tung Oy làm trục đối xứng.
- Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu: thì và f(-x) = - f(x).
Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng.
* Đối với hàm số lượng giác:
- Hàm số y = sinx là hàm số lẻ trên D = R.
- Hàm số y = cosx là hàm số chẵn trên D = R.
- Hàm số y = tanx là hàm số lẻ trên .
- Hàm số y = cotx là hàm số lẻ trên .
b) Tính tuần hoàn và chu kì của hàm số:
* Định nghĩa:
- Hàm số y = f(x) xác định trên tập hợp D, được gọi là hàm số tuần hoàn nếu có số sao cho với mọi ta có ; và f(x + T) = f(x).
- Nếu có số dương T nhỏ nhất thỏa mãn các điều kiện trên thì T gọi là chu kì của hàm tuần hoàn f.
* Đối với hàm số lượng giác:
Hàm số y = sinx; y = cosx tuần hoàn với chu kì .
Hàm số y = tanx; y = cotx tuần hoàn với chu kì .
2. Các dạng bài tập
Dạng 1. Xét tính chẵn, lẻ của hàm số lượng giác
Phương pháp giải:
Bước 1: Tìm tập xác định D của hàm số, khi đó:
- Nếu D là tập đối xứng (tức là ), ta thực hiện tiếp bước 2.
- Nếu D không phải là tập đối xứng (tức là mà ), ta kết luận hàm số không chẵn cũng không lẻ.
Bước 2: Xác định f(-x), khi đó:
- Nếu f(-x) = f(x) kết luận hàm số là hàm chẵn.
- Nếu f(-x) = - f(x) kết luận hàm số là hàm lẻ.
- Ngoài ra kết luận hàm số không chẵn cũng không lẻ.
Dạng 2: Xét tính tuần hoàn, tìm chu kỳ của hàm số lượng giác
Phương pháp giải:
- Xét tính tuần hoàn và chu kì bằng định nghĩa.
- Sử dụng các kết quả sau:
+ Hàm số y = sin(ax + b) là một hàm số tuần hoàn với chu kì .
+ Hàm số y = cos(ax + b) là một hàm số tuần hoàn với chu kì .
+ Hàm số y = tan(ax + b) là một hàm số tuần hoàn với chu kì .
+ Hàm số y = cot(ax + b) là một hàm số tuần hoàn với chu kì .
+ Nếu hàm số y = f(x) tuần hoàn với chu kì T thì hàm số y = Af(x) (với A khác 0) tuần hoàn với chu kì T.
+ Nếu hàm số y = f(x) tuần hoàn với chu kì T thì hàm số y = f(x) + c (c là hằng số) tuần hoàn với chu kì T.
+ Nếu hàm số y = f1(x); y = f2(x);… y = fn(x) tuần hoàn với chu kì lần lượt là T1; T2; … Tn thì hàm số tuần hoàn với chu kì T là bội chung nhỏ nhất của T1; T2; … Tn.
Xem thêm các bài viết liên quan hay, chi tiết:
Phương pháp xét tính chẵn, lẻ của hàm số chi tiết nhất
Xét tính chẵn, lẻ, chu kì tuần hoàn của hàm số lượng giác và cách giải
Câu 13:
23/07/2024Hàm số nào sau đây có đồ thị không là đường hình sin?
Xem đáp án
Các hàm số sin, cos đều có đồ thị là đường hình sin nên các đáp án A, B, C đều có đồ thị là đường hình sin.
Đáp án cần chọn là: D
Chú ý
Một số em có thể sẽ chọn nhầm đáp án B vì nghĩ rằng hàm số y = cosx không có đồ thị là đường hình sin là sai.
Câu 14:
22/07/2024Đường cong trong hình có thể là đồ thị của hàm số nào dưới đây?
Xem đáp án
Nhận xét:
Hàm số y=sinx và y=cosx có đồ thị hình sin nên loại.
Đường cong trên từng đoạn có hướng đi xuống nên hàm số nghịch biến trên mỗi đoạn đó.
Trong các đáp án đã cho thì chỉ có hàm số y=cotx có dạng đồ thị như trên.
Đáp án cần chọn là: A
Chú ý
Một số em có thể sẽ nhầm với đồ thị hàm số y=tanx và chọn nhầm đáp án B là sai.
Câu 15:
23/07/2024Đồ thị hàm số y=tanx nhận đường thẳng nào sau đây là tiệm cận?
Xem đáp án
Đồ thị hàm số y=tanx nhận các đường thẳng làm tiệm cận đứng.
Đáp án cần chọn là: C