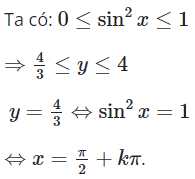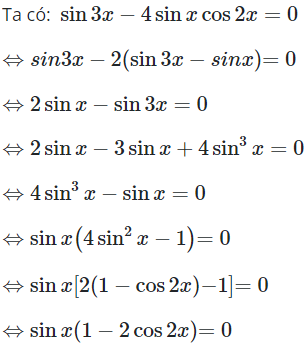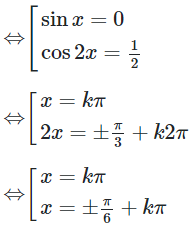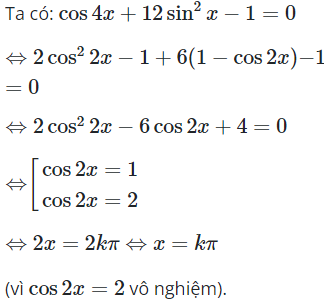Trắc nghiệm Toán 11 Ôn tập chương 1
-
692 lượt thi
-
24 câu hỏi
-
45 phút
Danh sách câu hỏi
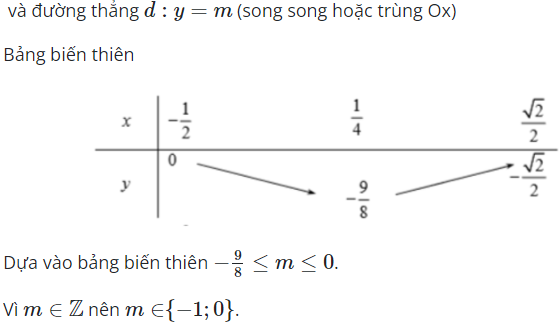
Câu 2:
23/07/2024Hàm số có tập xác định khi
Xem đáp án
Chọn D.
Hàm số có tập xác định luôn đúng nên nhận giá trị
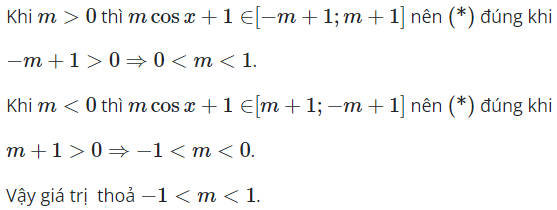
Câu 6:
14/11/2024Hàm số đồng biến trên khoảng:
Xem đáp án
Đáp án đúng là A.
Lời giải
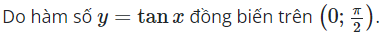
*Phương pháp giải:
Sử dụng kiến thức về đồng biến của hàm số lương giác
*Lý thuyết:
5. Đồ thị và tính chất của hàm số y = tanx
Tập xác định là .
Tập giá trị là .
Là hàm số lẻ và tuần hoàn chu kì .
Đồng biến trên mỗi khoảng , .
Có đồ thị đối xứng qua gốc tọa độ.
Xem thêm
Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2024 + Bài Tập) – Toán 12
Câu 7:
23/07/2024Khẳng định nào sau đây đúng?
Xem đáp án
Chọn D.
Do hàm số đồng biến trên
cho 
suy ra đồng biến trên
Câu 9:
23/07/2024Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
Xem đáp án
Chọn C.
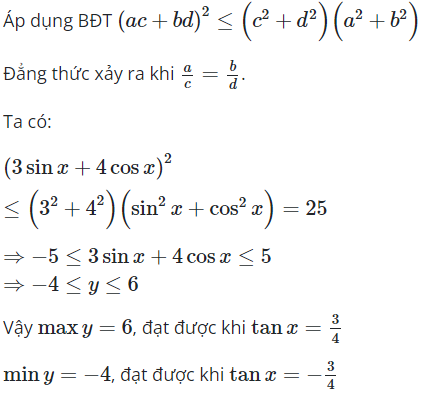
Chú ý: Với cách làm tương tự ta có được kết quả tổng quát sau
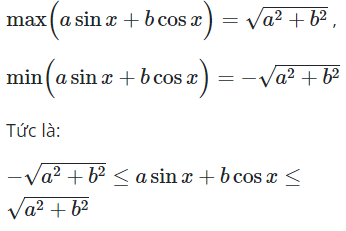
Câu 10:
16/07/2024Xét các phương trình lượng giác:
Trong các phương trình trên, phương trình nào vô nghiệm?
Xem đáp án
Chọn A
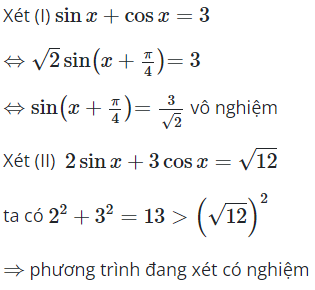
Câu 13:
23/07/2024Phương trình vô nghiệm khi và chỉ khi:
Xem đáp án
Chọn A
Phương trình vô nghiệm khi và chỉ khi:
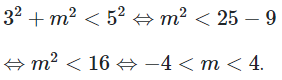
Câu 20:
08/11/2024Tính tổng tất cả các nghiệm của phương trình trên đoạn
Xem đáp án
Đáp án đúng là D
Lời giải
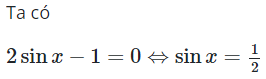
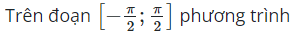
*Phương pháp giải
- đưa về phương trình sinx = a để giải bài toán và tìm nghiệm
*Lý thuyết
Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện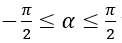 
và sinα = a thì ta viết α = arcsin a.
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π - arcsina + k2π, k ∈ Z.
Các trường hợp đặc biệt:
+ Khi a = 1: Phương trình sinx = 1 có các nghiệm là .
+ Khi a = – 1: Phương trình sinx = – 1 có các nghiệm là .
+ Khi a = 0: Phương trình sinx = 0 có các nghiệm là .
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:
at + b = 0 (1)
Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
Phương pháp: Chuyển vế rồi chia hai vế của phương trình (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.
Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.
- Phương pháp:
Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.
Xem thêm
Lý thuyết Phương trình lượng giác cơ bản – Toán 11
Toán 11 giải bài tập Bài 2 SGK: Phương trình lượng giác cơ
