Giải Toán 11 trang 86 Tập 1 Chân trời sáng tạo
Với giải bài tập Toán 11 trang 86 trong Bài tập cuối chương 3 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 86.
Giải Toán 11 trang 86 Tập 1
Bài 6 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) .
b) .
c) .
d) .
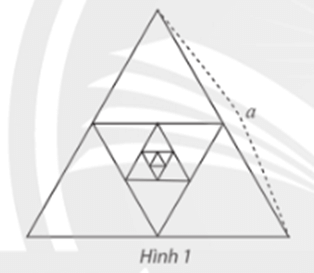
Tỉnh tổng chu vi và tổng diện tích của các tam giác của dãy.
Lời giải:
Ta có:
Diện tích tam giác H1 = S và chu vi tam giác H1 = 3a;
Diện tích tam giác H2 = S và chu vi tam giác H2 = 3a;
Diện tích tam giác H2 = S và chu vi tam giác H3 = 3a;
...
Diện tích tam giác Hn = S và chu vi tam giác H2 = 3a;
Khi đó:
Diện tích của dãy các tam giác H1; H2; H3; ...; H4 lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u1 = S và công bội q = có tổng bằng .
Diện tích của dãy các tam giác H1; H2; H3; ...; H4 lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u1 = 3a và công bội q = có tổng bằng
.
Bài 8 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) .
b) .
c) .
Bài 9 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) .
b) .
Bài 10 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) .
b) .
Bài 11 trang 86 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = 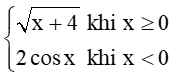
Lời giải:
+) Với x ∈ (0; + ∞) ta có f(x) = liên tục.
+) Với x ∈ (– ∞; 0) ta có f(x) = 2cosx liên tục.
+) Tại x = 0, ta có:
;
.
Suy ra
Do đó hàm số liên tục tại x = 0.
Vậy hàm số liên tục trên ℝ.
Bài 12 trang 86 Toán 11 Tập 1: Cho hàm số f(x) = 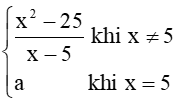
Lời giải:
+) Với mọi x ≠ 5 thì f(x) = liên tục.
+) Tại x = 5, ta có:
.
f(5) = a
Để hàm số liên tục trên ℝ thì hàm số phải liên tục tại x = 5 khi a = 10.
Biết rằng T(t) là hàm liên tục trên tập xác đinh. Tìm giá trị của k.
Lời giải:
+) Với 0 ≤ t < 60 thì T(t) = 10 + 2t là hàm số liên tục.
+) Với 60 < t ≤ 100 thì T(t) = k – 3t là hàm số liên tục.
+) Tại t = 60, ta có:
Để hàm số liên tục trên tập xác định [0; 100] thì hàm số liên tục tại x = 60
⇔ k – 180 = 130
⇔ k = 240.
Xem thêm lời giải bài tập Toán 11 sách Chân trời sáng tạo hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 85 Toán 11 Tập 1: lim bằng: A. 1; B. 0; C. 3; D. 2...
Bài 2 trang 85 Toán 11 Tập 1: Tổng của cấp số nhân lùi vô hạn: bằng...
Bài 3 trang 85 Toán 11 Tập 1: bằng A. 0; B. 6; C. 3; D. 1...
Bài 4 trang 85 Toán 11 Tập 1: Hàm số: f(x) = 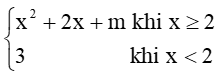
Bài 5 trang 85 Toán 11 Tập 1: bằng A. 2; B. – 1; C. 0; D. 1...
Bài 6 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau: a) ;...
Bài 8 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau: a) ;...
Bài 9 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau: a) ;...
Bài 10 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau: a) ;...
Bài 11 trang 86 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = 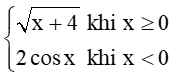
Bài 12 trang 86 Toán 11 Tập 1: Cho hàm số f(x) = 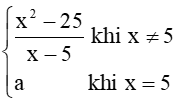
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo

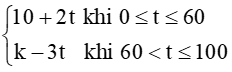 (k là hằng số).
(k là hằng số).