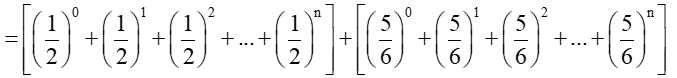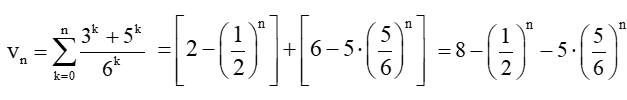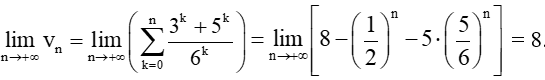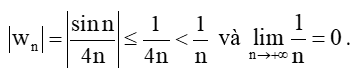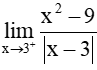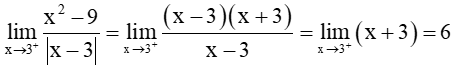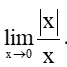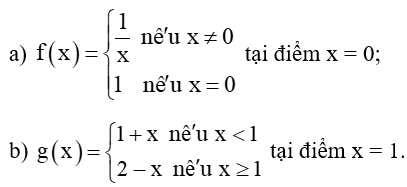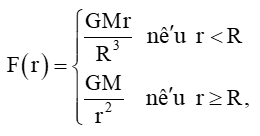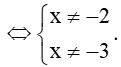Giải Toán 11 trang 124 Kết nối tri thức
Với giải bài tập Toán 11 trang 124 trong Bài tập cuối chương 5 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 124.
Giải Toán 11 trang 124
Lời giải:
Vì
Do đó, limn→+∞(un−1)=0. Từ đó suy ra limn→+∞un=1.
Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số sau:
Lời giải:
a) un=n23n2+7n−2
Ta có:
limn→+∞un=limn→+∞n23n2+7n−2=limn→+∞n2n2(3+7n−2n2)=limn→+∞13+7n−2n2=13
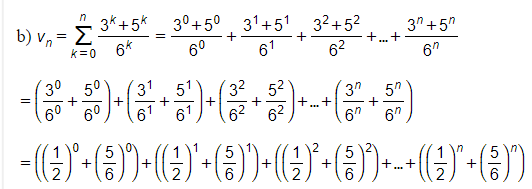
Vì (12)1+(12)2+...+(12)n là tổng n số hạng đầu của cấp số nhân với số hạng đầu là (12)1=12 và công bội là 12 nên
(12)0+(12)1+(12)2+...+(12)n=(12)0+12(1−(12)n)1−12=1+(1−(12)n)=2−(12)n.
Tương tự, ta tính được:
(56)0+(56)1+(56)2+...+(56)n=(56)0+56(1−(56)n)1−56=1+5(1−(56)n)=6−5⋅(56)n.
Do đó,
Vậy
c) wn=sinn4n
Ta có:
Do đó, limn→+∞wn=limn→+∞sinn4n=0.
Bài 5.27 trang 124 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số.
Lời giải:
a) Ta có: 1,(01) = 1,010101... = 1 + 0,01 + 0,0001 + 0,000001 + ...
= 100 + 10-2 + 10-4 + 10-6 + ...
Đây là tổng của cấp số nhân lùi vô hạn với u1 = 100 = 1 và q = 10-2 nên
1,(01) = u11−q=11−10−2=10099.
b) Ta có: 5,(132) = 5,132132132... = 5 + 0,132 + 0,000132 + 0,000000132 + ...
= 5 + 0,132 + 0,132 . 10-3 + 0,132 . 10-6 + ...
Vì 0,132 + 0,132 . 10-3 + 0,132 . 10-6 + ... là tổng của cấp số nhân lùi vô hạn với u1 = 0,132 và q = 10-3 nên
0,132 + 0,132 . 10-3 + 0,132 . 10-6 + ... = u11−q=0,1321−10−3=44333.
Do đó 5,(132) = 5 + 44333 = 1709333.
Bài 5.28 trang 124 Toán 11 Tập 1: Tính các giới hạn sau:
Lời giải:
a) limx→7√x+2−3x−7=limx→7(√x+2)2−32(x−7)(√x+2+3)
=limx→7x−7(x−7)(√x+2+3)=limx→71√x+2+3=1√7+2+3=16.
b) limx→1x3−1x2−1=limx→1(x−1)(x2+x+1)(x−1)(x+1)=limx→1x2+x+1x+1=12+1+11+1=32.
c) limx→12−x(1−x)2
Ta có: limx→1(2−x)=2−1=1>0;
limx→1(1−x)2=0 và (1 – x)2 > 0 với mọi x ≠ 1.
Do vậy, limx→12−x(1−x)2=+∞.
d) limx→−∞x+2√4x2+1=limx→−∞x+2√x2(4+1x2)
=limx→−∞x(1+2x)−x√4+1x2=limx→−∞−(1+2x)√4+1x2=−12.
Bài 5.29 trang 124 Toán 11 Tập 1: Tính các giới hạn một bên:
Lời giải:
a)
Với mọi x > 3, ta có x – 3 > 0 nên |x – 3| = x – 3.
Do đó,
b) limx→1−x√1−x
Ta có: limx→1−x=1>0; limx→1−√1−x=0
Và với mọi x < 1, ta có 1 – x > 0, suy ra √1−x>0.
Vậy limx→1−x√1−x=+∞.
Bài 5.30 trang 124 Toán 11 Tập 1: Chứng minh rằng giới hạn 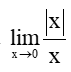
Lời giải:
+) Với x > 0, ta có: |x| = x.
Khi đó, 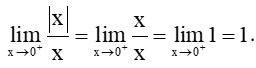
+) Với x < 0, ta có: |x| = – x.
Khi đó, 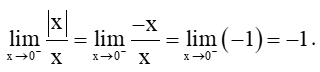
Từ (1) và (2) suy ra 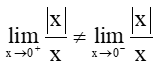
Bài 5.31 trang 124 Toán 11 Tập 1: Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho.
Lời giải:
a) Với x ≠ 0, thì f(x)=1x, ta có: limx→0−1x=−∞ và limx→0+1x=+∞.
Suy ra limx→0−1x≠limx→0+1x nên không tồn tại limx→01x.
Vậy hàm số đã cho gián đoạn tại x = 0.
b) Ta có: limx→1+f(x)=limx→1+(2−x)=2−1=1;
limx→1−f(x)=limx→1−(1+x)=1+1=2.
Suy ra nên không tồn tại limx→1f(x).
Vậy hàm số đã cho gian đoạn tại x = 1.
Lời giải:
Vì M và R lần lượt là khối lượng và bán kính của Trái Đất, G là hằng số hấp dẫn, do đó M, R, G đều khác 0, r là khoảng cách nên r > 0.
Ta có: 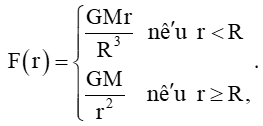
+) Với r < R thì F(r) = GMrR3 hay F(r) = GMR3.r là hàm đa thức nên nó liên tục trên (0; R).
+) Với r > R thì F(r) = GMr2 là hàm phân thức nên nó liên tục trên (R; +∞).
+) Tại r = R, ta có F(R) = GMR2.
limr→R+F(r)=limr→R+GMr2=GMR2; limr→R−f(R)=limr→R−GMrR3=GMRR3=GMR2.
Do đó, limr→R+F(r)=limr→R−F(r)=GMR2 nên limr→RF(r)=GMR2=F(R).
Suy ra hàm số F(r) liên tục tại r = R.
Vậy hàm số F(r) liên tục trên (0; +∞).
Lời giải:
a) Biểu thức có nghĩa khi x2 + 5x + 6 ≠ 0 ⇔ (x + 2)(x + 3) ≠ 0
Do đó, tập xác định của hàm số f(x) là ℝ \ {– 3; – 2} = (–∞; – 3) ∪ (– 3; – 2) ∪ (– 2; +∞).
Suy ra hàm số f(x) xác định trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞). Trên các khoảng này, tử thức (hàm lượng giác) và mẫu thức (hàm đa thức) là các hàm số liên tục. Vậy hàm số f(x)=cosxx2+5x+6 liên tục trên các khoảng xác định của chúng.
b) Biểu thức x−2sinx có nghĩa khi sin x ≠ 0 ⇔ x ≠ kπ, k ∈ ℤ.
Do đó, tập xác định của hàm số g(x) là ℝ \ {kπ | k ∈ ℤ}.
Trên các khoảng xác định của hàm số g(x), tử thức x – 2 (hàm đa thức) và mẫu thức sin x (hàm lượng giác) là các hàm số liên tục.
Vậy hàm số g(x)=x−2sinx liên tục trên các khoảng xác định của chúng.
Bài 5.34 trang 124 Toán 11 Tập 1: Tìm các giá trị của a để hàm số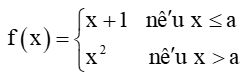
Lời giải:
Ta có: 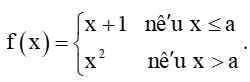
+) Với x < a thì f(x) = x + 1 là hàm đa thức nên nó liên tục trên (–∞; a).
+) Với x > a thì f(x) = x2 là hàm đa thức nên nó liên tục trên (a; +∞).
+) Tại x = a, ta có f(a) = a + 1.
limx→a−f(x)=limx→a−(x+1)=a+1; limx→a+f(x)=limx→a+x2=a2.
Để hàm số f(x) đã cho liên tục trên ℝ thì f(x) phải liên tục tại x = a, điều này xảy ra khi và chỉ khi limx→a+f(x)=limx→a−f(x)=f(a)⇔ a + 1 = a2 ⇔ a2 – a – 1 = 0
Suy ra a=1−√52 hoặc a=1+√52.
Vậy 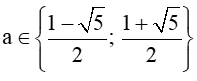
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 5.18 trang 123 Toán 11 Tập 1: Cho dãy số (un) với un=√n2+1−√n. Mệnh đề đúng là
Bài 5.19 trang 123 Toán 11 Tập 1: Cho un=2+22+...+2n2n. Giới hạn của dãy số (un) bằng...
Bài 5.21 trang 123 Toán 11 Tập 1: Cho hàm số f(x)=√x+1−√x+2. Mệnh đề đúng là
Bài 5.22 trang 123 Toán 11 Tập 1: Cho hàm số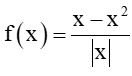
Bài 5.23 trang 123 Toán 11 Tập 1: Cho hàm số . Hàm số f(x) liên tục trên...
Bài 5.24 trang 123 Toán 11 Tập 1: Cho hàm số Hàm số 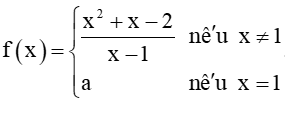
Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số sau: a) un=n23n2+7n−2;...
Bài 5.28 trang 124 Toán 11 Tập 1: Tính các giới hạn sau: a) limx→7√x+2−3x−7;...
Bài 5.29 trang 124 Toán 11 Tập 1: Tính các giới hạn một bên: a) 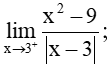
Bài 5.30 trang 124 Toán 11 Tập 1: Chứng minh rằng giới hạn 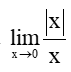
Bài 5.31 trang 124 Toán 11 Tập 1: Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho...
Bài 5.34 trang 124 Toán 11 Tập 1: Tìm các giá trị của a để hàm số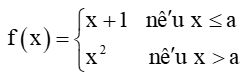
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức

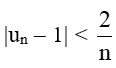 . Có kết luận gì về giới hạn của dãy số này?
. Có kết luận gì về giới hạn của dãy số này?