Giải Toán 10 trang 9 Tập 2 | Kết nối tri thức Giải Toán lớp 10

Giải Toán 10 trang 9 Tập 2

Luyện tập 3 trang 9 Toán 10 Tập 2: Vẽ đồ thị của các hàm số y = 3x + 1 và y = – 2x². Hãy cho biết:

a) Hàm số y = 3x + 1 đồng biến hay nghịch biến trên ℝ.

b) Hàm số y = – 2x² đồng biến hay nghịch biến trên mỗi khoảng: (– ∞; 0) và (0; + ∞).

Lời giải

Vẽ các đồ thị hàm số:

* Hàm số y = 3x + 1

Tập xác định của hàm số là ℝ.

Với x = 0 thì y = 3 . 0 + 1 = 1

Với x = – 1 thì y = 3 . (– 1) + 1 = – 2

Vậy đồ thị hàm số y = 3x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; – 2).

* Hàm số y = – 2x²

Tập xác định của hàm số là ℝ.

Bảng giá trị tương ứng của x và y

 

Trên mặt phẳng tọa độ, lấy năm điểm có tọa độ là (0; 0), (1; – 2), (– 1; – 2), (2; – 8), (– 2; – 8) rồi vẽ đường cong đi qua năm điểm trên ta được đồ thị của hàm số y = – 2x².

 

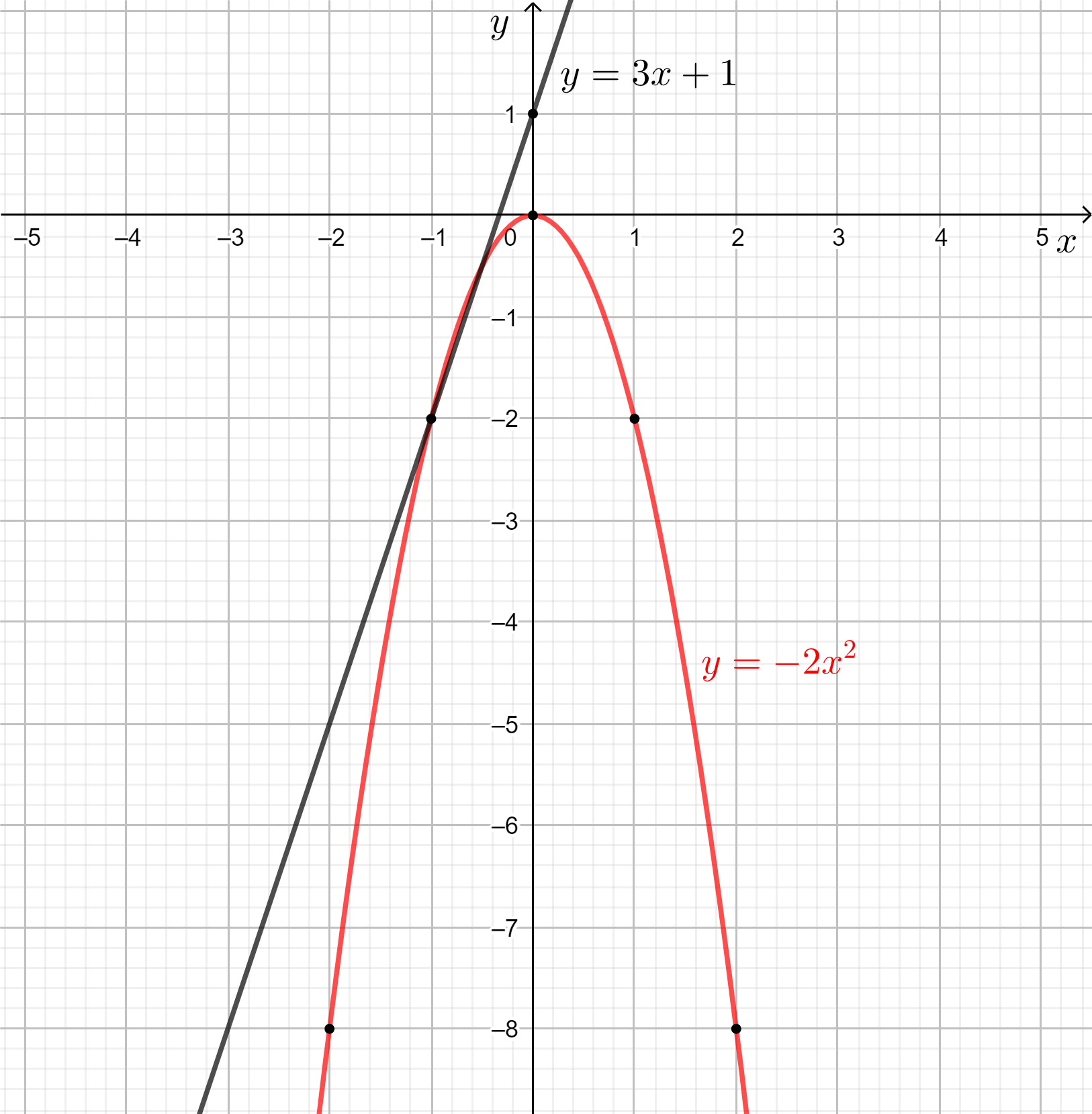
a) Từ hình trên trên, ta thấy đồ thị hàm số y = 3x + 1 đi lên từ trái sang phải trên ℝ nên hàm số y = 3x + 1 đồng biến trên ℝ.

b) Từ hình trên, ta có:

- Trên khoảng (– ∞; 0), đồ thị hàm số y = – 2x² đi lên từ trái sang phải nên hàm số đồng biến trên khoảng này.

- Trên khoảng (0; + ∞), đồ thị hàm số y = – 2x² đi xuống từ trái sang phải nên hàm số nghịch biến trên khoảng này.

Vận dụng 2 trang 9 Toán 10 Tập 2: Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.

 

a) Tính số tiền phải trả khi di chuyển 25 km.

b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.

c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.

Lời giải

a) Khi di chuyển 25 km thì khách hàng phải trả 10 000 đồng cho 0,6 km đầu tiên (giá mở cửa) và 13 000 đồng cho mỗi km của  24,4 km (25 – 0,6) sau (đây là giá tính cho km tiếp theo dưới 25 km).

Tổng số tiền phải trả khi di chuyển 25 km là: 10 000 + 24,4 . 13 000 = 327 200 (đồng).

Vậy số tiền phải trả khi di chuyển 25 km là 327 200 đồng.

b) Gọi x (km, x > 0) là độ dài quãng đường di chuyển và y (đồng) là số tiền phải trả tương ứng.

Từ bảng giá cước, ta có:

- Giá mở cửa là 10 000 đồng cho 0,6 km đầu tiên, có nghĩa là khi x ≤ 0,6 thì số tiền phải trả tương ứng là y = 10 000.

- Giá tiền cho km tiếp theo đến dưới 25 km là 13 000 đồng cho mỗi km, có nghĩa là khi 0,6 < x ≤ 25 thì số tiền phải tương ứng là y = 10 000 + 13 000(x – 0,6) hay y = 13 000x + 2 200.

- Giá tiền phải trả cho km thứ 25 trở lên là 11 000 đồng cho mỗi km, có nghĩa là khi x > 25 thì số tiền phải trả tương ứng là y = 10 000 + 13 000 . 24,4 + 11 000(x – 25) hay y = 11 000 x + 52 200.

Vậy ta có công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển là:

$y=\left\{\begin{array}{l}10\mathrm{000,}x\le \mathrm{0,6}\\ 13000x+2\mathrm{200,}\mathrm{0,6}<x\le 25\\ 11000x+52\mathrm{200,}x>25.\end{array}\right.$

c) Ta vẽ đồ thị hàm số $y=\left\{\begin{array}{l}10\mathrm{000,}x\le \mathrm{0,6}\\ 13000x+2\mathrm{200,}\mathrm{0,6}<x\le 25\\ 11000x+52\mathrm{200,}x>25\end{array}\right.$.

Để vẽ đồ thị hàm số trên, ta vẽ các đồ thị y = 10 000 trên (0; 0,6], đồ thị y = 13 000x + 2 200 trên (0,6; 25] và đồ thị y = 11 000x + 52 200 trên (25; + ∞), mỗi đồ thị cần vẽ là một đoạn thẳng trên khoảng tương ứng.

Vậy ta vẽ được đồ thị hàm số trên:

 

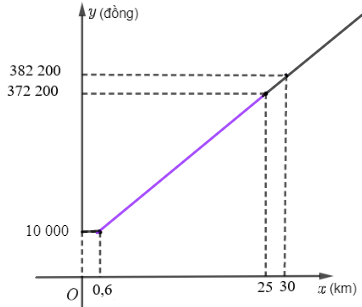
Từ hình trên, ta thấy đồ thị hàm số $y=\left\{\begin{array}{l}10\mathrm{000,}x\le \mathrm{0,6}\\ 13000x+2\mathrm{200,}\mathrm{0,6}<x\le 25\\ 11000x+52\mathrm{200,}x>25\end{array}\right.$ đi lên từ trái sang phải trên (0,6; + ∞).

Vậy hàm số này đồng biến trên (0,6; + ∞).

B. Bài tập

Bài 6.1 trang 9 Toán 10 Tập 2: Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x?

a) x + y = 1;

b) y = x²;

c) y² = x;

d) x² – y² = 0.

Lời giải

a) Ta có: x + y = 1 ⇒ y = – x + 1.

Với mỗi giá trị thực của x, ta đều xác định được duy nhất một giá trị thực của y.

Vậy y là hàm số của x.

b) y = x²

Với mỗi giá trị thực của x, ta đều xác định được duy nhất một giá trị thực của y.

Vậy y là hàm số của x.

c) y² = x

Với x = 1 thì y² = 1, khi đó y = 1 hoặc y = – 1 nên với một giá trị của x, ta xác định được hai giá trị của y tương ứng, vậy y không phải là hàm số của x.

d) x² – y² = 0 ⇔ y² = x².

Với x = 1 ⇒ x² = 1² = 1, do đó y² = 1 nên y = 1 hoặc y = – 1, do đó với một giá trị của x, ta xác định được hai giá trị của y tương ứng, vậy y không phải là hàm số của x.

Bài 6.2 trang 9 Toán 10 Tập 2: Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.

Lời giải

Có nhiều ví dụ, chẳng hạn ta có bảng 8 số nguyên tố đầu tiên:

 

Tập xác định là D = {1; 2; 3; 4; 5; 6; 7; 8}.

Tập giá trị là {2; 3; 5; 7; 11; 13; 17; 19}.

Bài 6.3 trang 9 Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:

a) y = 2x³ + 3x + 1;

b) $y=\frac{x-1}{x^2-3x+2}$;

c) $y=\sqrt{x+1}+\sqrt{1-x}$.

Lời giải

a) Biểu thức 2x³ + 3x + 1 có nghĩa với mọi số thực x.

Vậy tập xác định của hàm số là D = ℝ.

b) Biểu thức $\frac{x-1}{x^2-3x+2}$có nghĩa khi x² – 3x + 2 ≠ 0

⇔ x² – x – 2x + 2 ≠ 0

⇔ x(x – 1) – 2(x – 1) ≠ 0

⇔ (x – 1)(x – 2) ≠ 0

⇔ x – 1 ≠ 0 và x – 2 ≠ 0

⇔ x ≠ 1 và x ≠ 2.

Vậy tập xác định của hàm số là D = ℝ\{1; 2}.

c) Biểu thức $\sqrt{x+1}+\sqrt{1-x}$ có nghĩa khi $\left\{\begin{array}{l}x+1\ge 0\\ 1-x\ge 0\end{array}\right.$$\iff \left\{\begin{array}{l}x\ge -1\\ x\le 1\end{array}\right.\iff -1\le x\le 1$

Vậy tập xác định của hàm số là D = [– 1; 1].

Bài 6.4 trang 9 Toán 10 Tập 2: Tìm tập xác định và tập giá trị của mỗi hàm số sau:

a) y = 2x + 3;

b) y = 2x².

Lời giải

a) y = 2x + 3

Biểu thức 2x + 3 có nghĩa với mọi số thực x.

Vậy tập xác định của hàm số là D = $ℝ$.

Với mỗi giá trị bất kì của x, ta đều tìm được một giá trị của y tương ứng.

Vậy tập giá trị của hàm số là ℝ.

b) y = 2x²

Biểu thức 2x² có nghĩa với mọi số thực x.

Vậy tập xác định của hàm số này là D = ℝ.

Ta có: x² ≥ 0 với mọi x ∈ ℝ.

Do đó 2x² ≥ 0 với mọi x ∈ ℝ.

Vậy tập giá trị của hàm số trên là [0; + ∞).   

Bài 6.5 trang 9 Toán 10 Tập 2: Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.

a) y = – 2x + 1;

b) $y=-\frac{1}{2}{x}^2$.

Lời giải

a) y = – 2x + 1

Tập xác định của hàm số này là D = ℝ.

Với x = 0 thì y = 1, với x = 1 thì y = – 1.

Đồ thị hàm số y = – 2x + 1 là đường thẳng đi qua 2 điểm (0; 1) và (1; – 1).

 

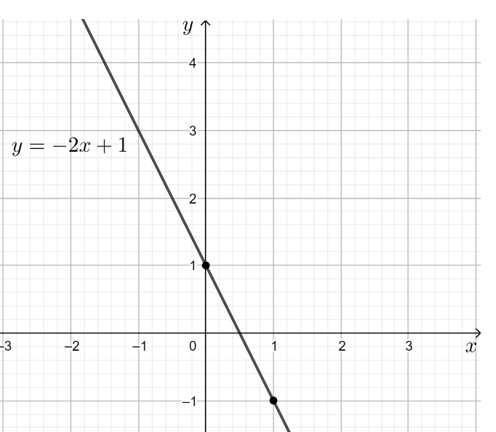
Đồ thị hàm số đi xuống từ trái qua phải trên ℝ nên hàm số nghịch biến trên ℝ.

b) $y=-\frac{1}{2}{x}^2$

Tập xác định của hàm số này là D = ℝ.

Bảng giá trị của x và y tương ứng:

x	0	1	– 1	2	– 2
y	0	$-\frac{1}{2}$	$-\frac{1}{2}$	– 2	– 2

Đồ thị hàm số $y=-\frac{1}{2}{x}^2$ là đường cong đi qua 5 điểm (0; 0), $\left(1;-\frac{1}{2}\right),\left(-1;-\frac{1}{2}\right)$, (2; – 2), (– 2; – 2).

 

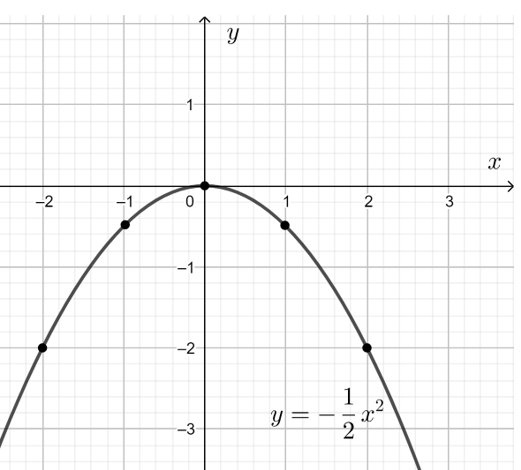
Ta thấy đồ thị hàm số đi lên từ trái sang phải trên (– ∞; 0) và đi xuống từ trái sang phải trên (0; + ∞).

Vậy hàm số đồng biến trên khoảng (– ∞; 0) và nghịch biến trên khoảng (0; + ∞).

Bài 6.6 trang 9 Toán 10 Tập 2: Giá thuê xe ô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và 900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe.

a) Viết công thức của hàm số T = T(x).

b) Tính T(2), T(3), T(5) và cho biết ý nghĩa của mỗi giá trị này.

Lời giải

a) Đổi: 1,2 triệu đồng = 1 200 000 đồng; 900 nghìn đồng = 900 000 đồng.

Gọi số ngày khách thuê xe là x (ngày), số tiền khách phải trả tương ứng là T (đồng).

Giá xe cho mỗi ngày trong 2 ngày đầu tiên là 1 200 000 đồng nên khi x ≤ 2 thì số tiền phải trả là: T = 1 200 000x.

Giá tiền khách phải trả khi thuê 2 ngày đầu là: 1 200 000 . 2 = 2 400 000 (đồng).

Khách thuê tiếp sau 2 ngày đầu, giá xe cho mỗi ngày trong các ngày tiếp theo là 900 000 đồng, hay với x > 2 thì số tiền phải trả là: T = 2 400 000 + 900 000(x – 2).

Vậy ta có hàm số $T=\left\{\begin{array}{l}1200000xn{ê}^{\text{'}}ux\le 2\\ 2400000+900000\left(x-2\right)n{ê}^{\text{'}}ux>2.\end{array}\right.$

b)

T(2) = 1 200 000 . 2 = 2 400 000, khách sẽ phải trả 2 400 000 đồng nếu thuê xe 2 ngày;

T(3) = 2 400 000 + 900 000.(3 – 2) = 3 300 000, khách sẽ phải trả 3 300 000 đồng nếu thuê xe 3 ngày;

T(5) = 2 400 000 + 900 000.(5 – 2) = 5 100 000, khách sẽ phải trả 5 100 000 đồng nếu thuê xe 5 ngày.

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Giải Toán 10 trang 5 Tập 2

Giải Toán 10 trang 6 Tập 2

Giải Toán 10 trang 7 Tập 2

Giải Toán 10 trang 8 Tập 2

Giải Toán 10 trang 9 Tập 2

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

Bài 16: Hàm số bậc hai

Bài 17: Dấu của tam thức bậc hai

Bài 18: Phương trình quy về phương trình bậc hai

Bài tập cuối chương 6

Bài 19: Phương trình đường thẳng