Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 45 Tập 2 Kết nối tri thức

    Với giải bài tập Toán lớp 10 trang 45 Tập 2 trong Bài 21: Đường tròn trong mặt phẳng tọa độ sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 45 Tập 2.

    1 778 10/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 45 Tập 2

    Luyện tập 3 trang 45 Toán 10 Tập 2:

    Viết phương trình đường tròn (C) đi qua ba điểm M(4; –5), N(2; –1), P(3; –8)

    Lời giải

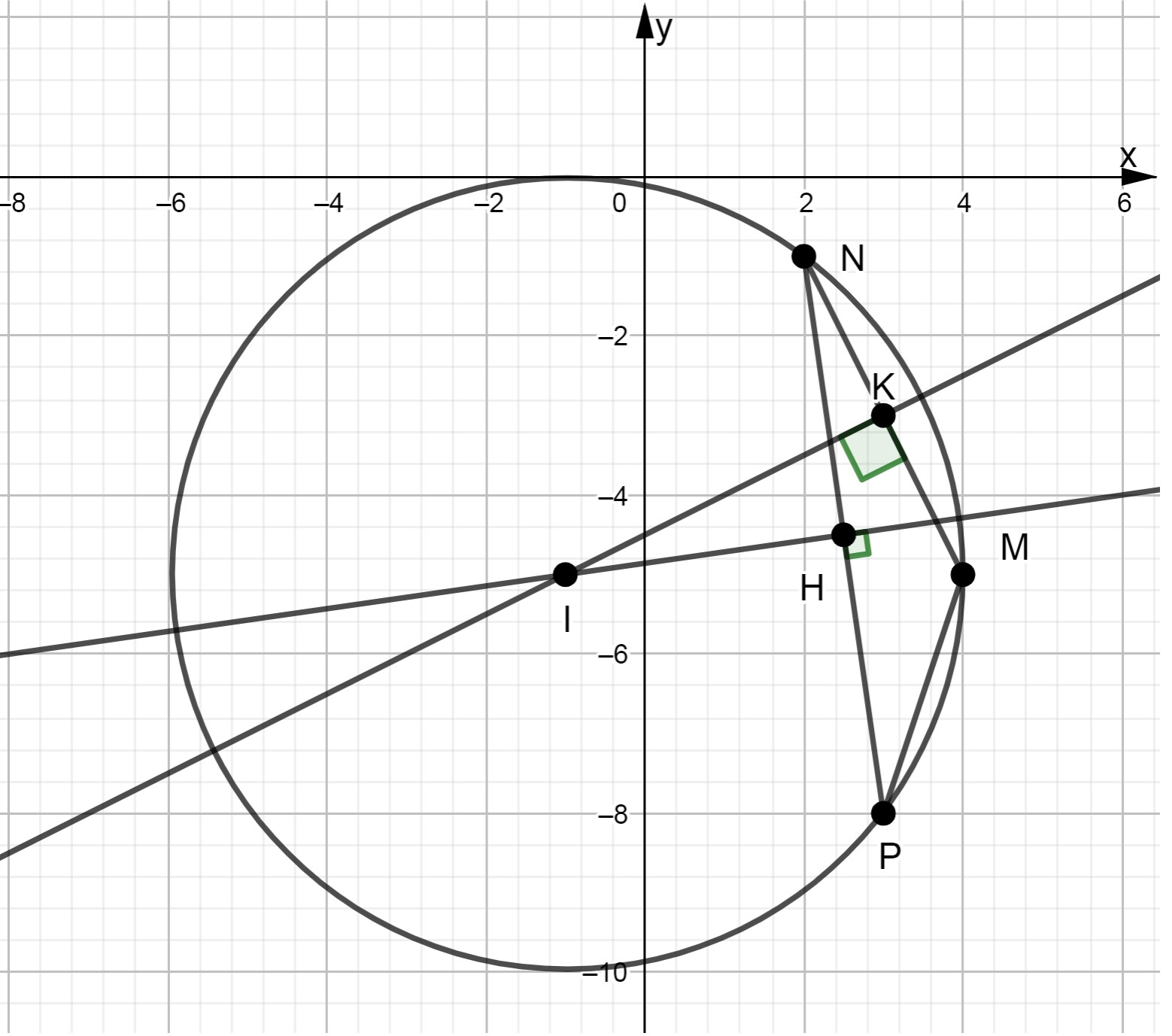
    Giải Toán 10 Bài 21 (Kết nối tri thức): Đường tròn trong mặt phẳng tọa độ (ảnh 1) 

    Gọi H và K lần lượt là trung điểm NP và MN

    Do đó toạ độ điểm H là xH=2+32=52yH=−1−82=−92 ⇒ H52;−92

    Toạ độ điểm K là xK=2+42=3yK=−5−12=−3 ⇒ K(3; –3)

    Gọi ∆1; ∆2 lần lượt là đường trung trực của NP; MN

    Vì đường thẳng ∆1 ⊥ NP nên đường thẳng ∆1 nhận vectơ NP→ = (1; – 7) làm vectơ pháp tuyến

    Phương trình đường thẳng ∆1 đi qua điểm H52;−92 và có vectơ pháp tuyến NP→ là:

    1.x−52−7y+92=0 hay x – 7y – 34 = 0

    Tương tự ta có đường thẳng ∆2 nhận vectơ MN→ = (–2; 4) làm vectơ pháp tuyến

    Phương trình đường thẳng ∆2 đi qua điểm K(3; –3) và có vectơ pháp tuyến MN→ là:

    –2.(x – 3) + 4.(y + 3) = 0 ⇔ –2x + 4y + 18 = 0 hay –x + 2y + 9 = 0.

    Gọi I là giao điểm của hai đường thẳng ∆1; ∆2. Do đó ,toạ độ điểm I thoả mãn hệ phương trình : x−7y−34=0−x+2y+9=0

    Cộng hai phương trình trong hệ trên vế theo vế ta được: –5y – 25 = 0 ⇒ y = –5

    Thay y = –5 vào phương trình –x + 2y + 9 = 0 ta được : –x + 2(–5) + 9 = 0

                                            ⇒ –x – 1 = 0 ⇒  x = –1

    Suy ra tâm I của đường tròn đi qua ba điểm M, N, P là I (–1; –5) và bán kính

    R = IM = 52+02=5

    Vậy phương trình đường tròn (C) là: (x +1)2 + (y + 5)2 = 25.

    Vận dụng  trang 45 Toán 10 Tập 2:

    Bên trong một hồ bơi, người ta dự định thiết kế hai bể sục nửa hình tròn bằng nhau và một bể sục hình tròn (H.7.14) để người bơi có thể ngồi dựa lưng vào thành các bể sục thư giãn. Hãy tìm bán kính của các bể sục để tổng chu vi của ba bể là 32 m mà tổng diện tích (chiếm hồ bơi) là nhỏ nhất. Trong tính toán, lấy π ≈ 3,14, độ dài tính theo mét và làm tròn tới chữ số thập phân thứ hai

    Lời giải

    Gọi x và y (m) lần lượt là bán kính của bể hình tròn và bể nửa hình tròn

    Chu vi một nửa hình tròn bán kính y là: πy + 2y = (π + 2)y (m)

    Khi đó chu vi của hai nửa hình tròn bán kính y là: 2(π + 2)y (m)

    Chu vi của hình tròn bán kính x là: 2πx (m)

    Theo giả thiết tổng chu vi của ba bể là 32 m nên 2πx + 2(π + 2)y = 32

                                                                            hay 1,57x + 2,57y – 8 = 0

    Gọi tổng diện tích ba bể sục là S (m2). Khi đó: πx2 + πy2 = S

    ⇒ x2 + y2 = Sπ= S3,14.

    Trong hệ trục toạ độ Oxy xét đường tròn (C) : x2 + y2 = S3,14 có tâm O(0; 0), bán kính R = S3,14 và đường thẳng ∆: 1,57x + 2,57y – 8 = 0

    Để S là nhỏ nhất thì khi đó bài toán trở thành: Tìm R nhỏ nhất để (C) và ∆ có ít nhất một điểm chung với hoành độ và tung độ đều là các số dương

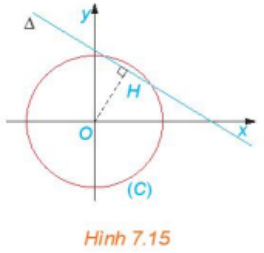
    Giải Toán 10 Bài 21 (Kết nối tri thức): Đường tròn trong mặt phẳng tọa độ (ảnh 1) 

    Để (C) và d có ít nhất một điểm chung thì d(O; ∆) ≤ R

    Ta có: d((O; ∆) = 1,57.0 + 2,57.0 – 8(1,57)2+(2,57)2 ≈ 2,66  ⇒ R ≥ 2,66

    Dấu “=” xảy ra khi đường tròn (C) tiếp xúc với đường thẳng ∆. Do đó, GTNN của R = 2,66

    Do đó, ta có hệ phương trình sau: 1,57x+2,57y−8=0(1)x2+y2=2,662(2)

    Từ phương trình (1) ta có:  x=8−2,57y1,57

    Thay x vào phương trình (2) ta được: 8−2,57y1,572+y2=2,662 

    ⇔ 2,572.y2 – 2.8.2,57.y + 82 + 1,572.y2 = 2,662.1,572

    ⇔ (2,572+1,572)y2−2.8.2,57y+64−2,662.1,572=0

    ⇔ y1≈2,34y2≈2,19⇒x1≈1,27x2≈1,51

    Vậy để diện tích của các bể sục là nhỏ nhất thì bán kính của bể hình tròn và bể nửa hình tròn lần lượt là 1, 27m và 2,34m hoặc 1,51 m và 2,19 m

    Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Giải Toán 10 trang 43 Tập 2

    Giải Toán 10 trang 44 Tập 2

    Giải Toán 10 trang 45 Tập 2

    Giải Toán 10 trang 46 Tập 2

    Giải Toán 10 trang 47 Tập 2

    Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Bài 22: Ba đường Conic

    Bài tập cuối chương 7

    Bài 23: Quy tắc đếm

    Bài 24: Hoán vị, chỉnh hợp và tổ hợp

    Bài 25: Nhị thức Newton

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 778 10/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: