Giải SBT Toán 10 trang 30 Tập 1 Cánh diều

Giải SBT Toán 10 trang 30 Tập 1 Cánh diều

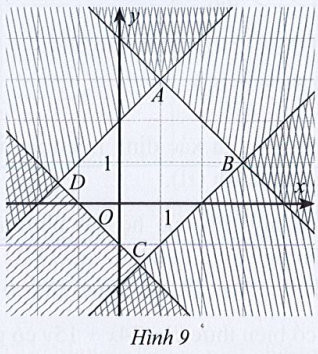
Bài 13 trang 30 SBT Toán 10 Tập 1: Miền đa giác ABCD ở Hình 9 là miền nghiệm của hệ bất phương trình:

A. $\left\{\begin{array}{l}x+y\le 4\\ x+y\ge -1\\ x-y\le 2\\ x-y\ge -2\end{array}\right.$.

B. $\left\{\begin{array}{l}x-y\le 4\\ x-y\ge -1\\ x+y\le 2\\ x+y\ge -2\end{array}\right.$.

C. $\left\{\begin{array}{l}x+y\le 1\\ x+y\ge -4\\ x-y\le 2\\ x-y\ge -2\end{array}\right.$.

D. $\left\{\begin{array}{l}x-y\le 1\\ x-y\ge -4\\ x+y\le 2\\ x+y\ge -2\end{array}\right.$.

Lời giải:

Đáp án đúng là A

+) Gọi d₁ là đường thẳng đi qua hai điểm A và D. Đường thẳng cắt hai trục tọa độ tại hai điểm (– 2; 0) và (0; 2) nên phương trình đường thẳng d là: $\frac{x}{-2}+\frac{y}{2}=1\iff x-y=-2$.

Lấy điểm O(0; 0) ta có 0 – 0 = 0 > – 2.

Mà điểm O thuộc miền nghiệm của hệ bất phương trình nên ta có bất phương trình x – y ≥  – 2.

+) Gọi d₂ là đường thẳng đi qua hai điểm A và D. Đường thẳng cắt hai trục tọa độ tại hai điểm (4; 0) và (0; 4) nên phương trình đường thẳng d là: $\frac{x}{4}+\frac{y}{4}=1\iff x+y=4$.

Lấy điểm O(0; 0) ta có 0 + 0 = 0 < 4.

Mà điểm O thuộc miền nghiệm của hệ bất phương trình nên ta có bất phương trình x + y ≤ 4.

+) Gọi d₃ là đường thẳng đi qua hai điểm B và C. Đường thẳng cắt hai trục tọa độ tại hai điểm (2; 0) và (0; – 2) nên phương trình đường thẳng d là: $\frac{x}{2}+\frac{y}{-2}=1\iff x-y=2$.

Lấy điểm O(0; 0) ta có 0 – 0 = 0 < 2.

Mà điểm O thuộc miền nghiệm của hệ bất phương trình nên ta có bất phương trình x – y ≤ 2.

+) Gọi d₄ là đường thẳng đi qua hai điểm D và C. Đường thẳng cắt hai trục tọa độ tại hai điểm (– 1; 0) và (0; – 1) nên phương trình đường thẳng d là: $\frac{x}{-1}+\frac{y}{-1}=1\iff x+y=-1$.

Lấy điểm O(0; 0) ta có 0 + 0 = 0 > – 1.

Mà điểm O thuộc miền nghiệm của hệ bất phương trình nên ta có bất phương trình x +  y ≥ – 1.

Từ đó ta có hệ bất phương trình sau: $\left\{\begin{array}{l}x-y\ge -2\\ x+y\le 4\\ x-y\le 2\\ x+y\ge -1\end{array}\right.$.

Bài 14 trang 30 SBT Toán 10 Tập 1: Giá trị nhỏ nhất của biểu thức F = – x + y trên miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-2x+y\le 2\\ -x+2y\ge 4\\ x+y\le 5\end{array}\right.$.

A. 0;

B. 1;

C. 2;

D. 3.

Lời giải:

Đáp án đúng là B

Bài toán đã cho trở thành tìm nghiệm (x; y) của hệ bất phương trình $\left\{\begin{array}{l}-2x+y\le 2\\ -x+2y\ge 4\\ x+y\le 5\end{array}\right.$ sao cho biểu thức F = – x + y đạt giá trị nhỏ nhất.

Trước hết ta xác định miền nghiệm của hệ bất phương trình đã cho:

Ta có ba đường thẳng: d₁: – 2x + y = 2; d₂: – x + 2y = 4 và d₃: x + y = 5.

+) Lấy O(0; 0) có – 2.0 + 0 = 0 < 2. Do đó miền nghiệm của bất phương trình – 2x + y ≤ 2 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₁.

+) Lấy O(0; 0) có – 0 + 2.0 = 0 < 4. Do đó miền nghiệm của bất phương trình – x + 2y ≥ 4 là nửa mặt phẳng không chứa điểm O(0; 0) có bờ là đường thẳng d₂.

+) Lấy O(0; 0) có 0 + 0 = 0 < 5. Do đó miền nghiệm của bất phương trình x + y ≤ 5 là nửa mặt phẳng chứa điểm O(0; 0) và có bờ là đường thẳng d₃.

Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(0; 2), B(1; 4) và C(2; 3) như trong hình vẽ sau:

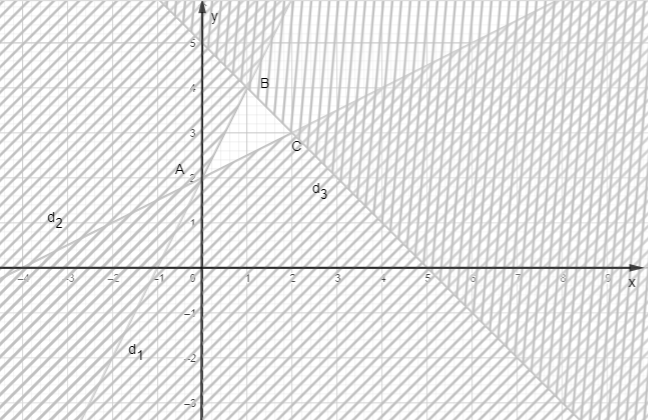
Ta đã chứng minh được biểu thức F = – x + y có giá trị nhỏ nhất tại các đỉnh của tam giác ABC.

Tại điểm A, với x = 0, y = 2 thì F = – 0 + 2 = 2.

Tại điểm B, với x = 1, y = 4 thì F = – 1 + 4 = 3.

Tại điểm C, với x = 2, y = 3 thì F = – 2 + 3 = 1.

Vậy giá trị nhỏ nhất của biểu thức F là 1 khi x = 2 và y = 3.

Bài 15 trang 30 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của hệ bất phương trình sau:

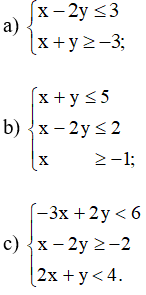
Lời giải:

a) Ta có hai đường thẳng: d₁: x – 2y = 3; d₂: x + y = – 3.

+) Lấy O(0; 0) không thuộc vào đường thẳng d₁ có 0 – 2.0 = 0 < 3. Do đó miền nghiệm của bất phương trình x – 2y ≤ 3 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₁.

+) Lấy O(0; 0) không thuộc đường thẳng d₂ có 0 + 0 = 0 > – 3. Do đó miền nghiệm của bất phương trình x + y ≥ – 3 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₂.

Miền nghiệm của hệ bất phương trình là miền không tô màu như trong hình vẽ sau:

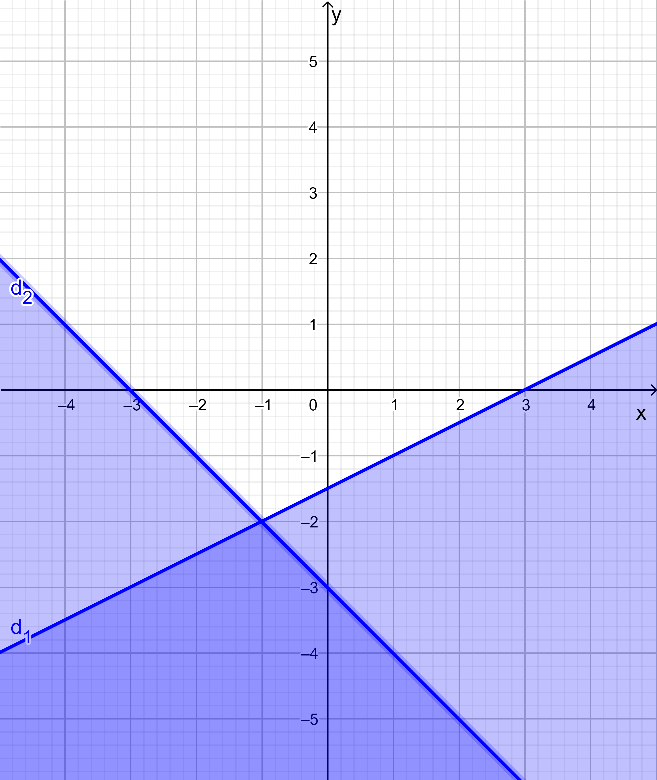
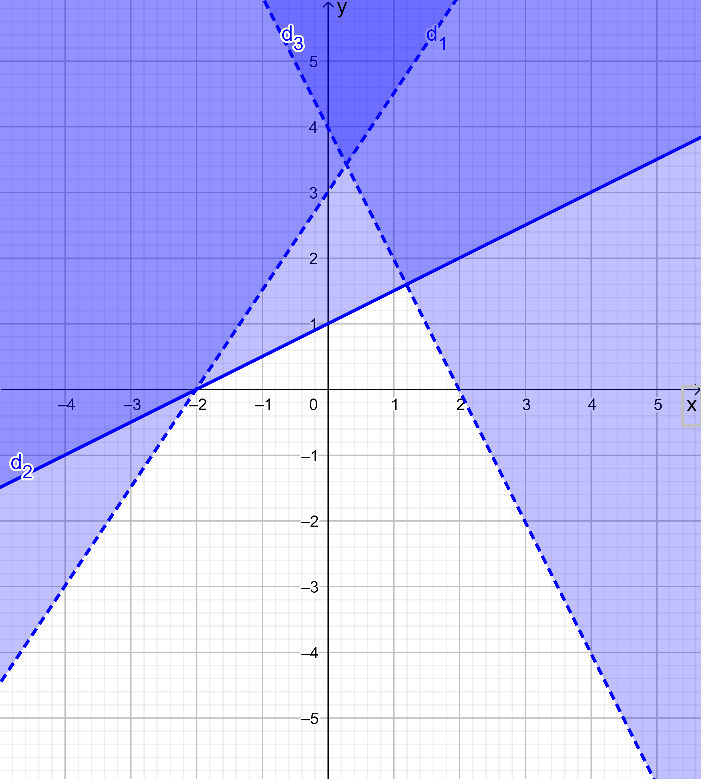
b) Ta có ba đường thẳng: d₁: x + y = 5; d₂: x – 2y = 2 và d₃: x = – 1.

+) Lấy O(0; 0) không thuộc đường thẳng d₁ có 0 + 0 = 0 < 5. Do đó miền nghiệm của bất phương trình x + y ≤ 5 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₁.

+) Lấy O(0; 0) không thuộc đường thẳng d₂ có 0 – 2.0 = 0 < 2. Do đó miền nghiệm của bất phương trình x – 2y ≤ 2 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₂.

+) Lấy O(0; 0) không thuộc đường thẳng d₃ có 0 ≥ – 1. Do đó miền nghiệm của bất phương trình x ≥ – 1 là nửa mặt phẳng chứa điểm O(0; 0) và có bờ là đường thẳng d₃.

Miền nghiệm của hệ bất phương trình được biểu diễn là phần không tô màu như trong hình vẽ sau:

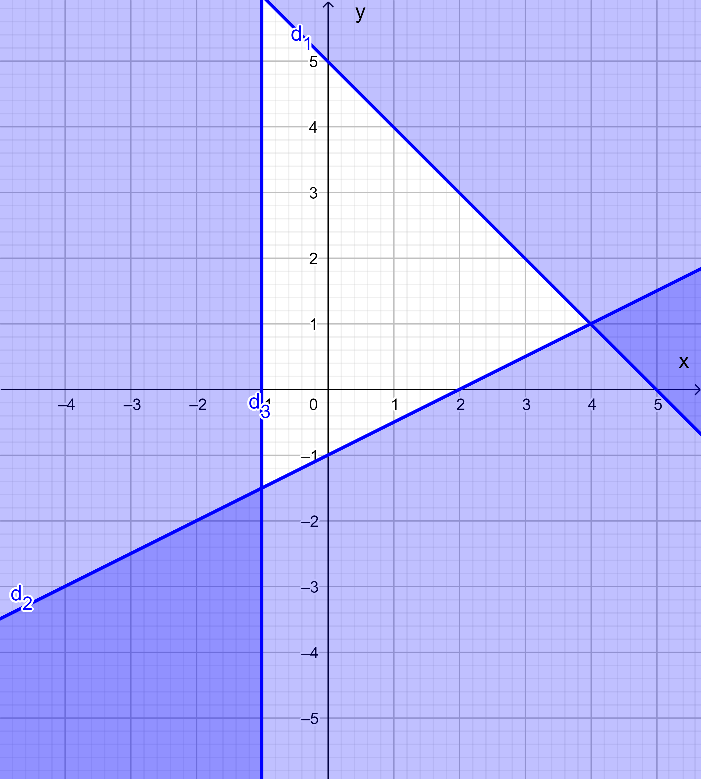
c) Ta có ba đường thẳng: d₁: – 3x + 2y = 6; d₂: x – 2y = – 2 và d₃: 2x + y = 4.

+) Lấy O(0; 0) không thuộc đường thẳng d₁ có – 3.0 + 2.0 = 0 < 6. Do đó miền nghiệm của bất phương trình – 3x + 2y < 6 là nửa mặt phẳng chứa điểm O(0; 0) không kể bờ là đường thẳng d₁ .

+) Lấy O(0; 0) không thuộc đường thẳng d₂ có 0 – 2.0 = 0 > – 2 . Do đó miền nghiệm của bất phương trình x – 2y ≥ – 2 là nửa mặt phẳng chứa điểm O(0; 0) có bờ là đường thẳng d₂.

+) Lấy O(0; 0) không thuộc đường thẳng d₃ có 2.0 + 0 < 4. Do đó miền nghiệm của bất phương trình 2x + y < 4 là nửa mặt phẳng chứa điểm O(0; 0) và không kể bờ là đường thẳng d₃.

Miền nghiệm của hệ bất phương trình được biểu diễn là miền không tô màu như trong hình vẽ sau:

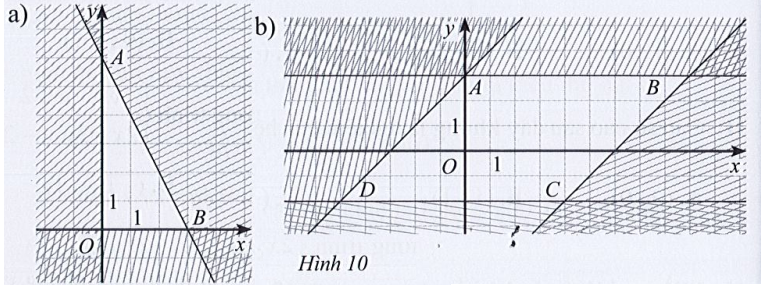
Bài 16 trang 30 SBT Toán 10 Tập 1: Viết hệ bất phương trình bậc nhất hai ẩn có miền nghiệm là miền đa giác không bị gạch ở mỗi Hình 10a, 10b.

Lời giải:

Xét Hình 10a):

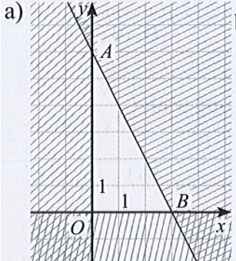
Ta có: Đường thẳng d₁ đi qua hai điểm O và A là trục tung Oy có phương trình x = 0.

Ta thấy điểm B thuộc miền nghiệm nằm bên phải trục tung nên điểm B thỏa mãn bất phương trình x ≥ 0 (1)

Đường thẳng d₂ đi qua hai điểm O và B là trục hoành Ox có phương trình y = 0.

Ta thấy điểm B thuộc miền nghiệm nằm trên trục hoành nên điểm B thỏa mãn bất phương trình y ≥ 0 (2)

Đường thẳng d₃ đi qua hai điểm A(0; 6) và B(3; 0) có phương trình là: $\frac{x}{3}+\frac{y}{6}=1\iff 2x+y=6$.

Ta thấy điểm O(0; 0) có 2.0 + 0 = 0 < 6 thuộc miền nghiệm nên điểm O thỏa mãn bất phương trình 2x + y ≤ 6 (3).

Từ (1), (2) và (3) miền nghiệm tam giác OAB biểu diễn cho hệ bất phương trình:

$\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 2x+y\le 6\end{array}\right.$.

Xét Hình 10b):

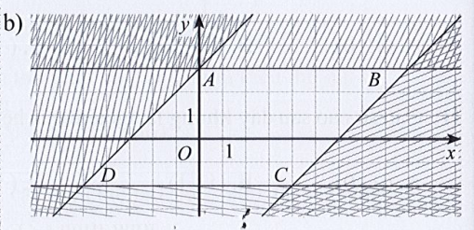
Ta có: Đường thẳng d₁ đi qua hai điểm A(0; 3) và B(9; 3) song song với trục hoành có phương trình y = 3.

Ta thấy điểm O thuộc miền nghiệm có 0 < 3 nên điểm O thỏa mãn bất phương trình y ≤ 3 (1)

Đường thẳng d₂ đi qua hai điểm A(0; 3) và D(– 5; – 2) cắt hai trục tọa độ Ox và Oy lần lượt tại các điểm có tọa độ là (– 3; 0) và (0; 3) có phương trình là: $\frac{x}{-3}+\frac{y}{3}=1\iff x-y=-3$.

Ta thấy điểm O thuộc miền nghiệm có 0 – 0 = 0 > – 3 nên điểm O thỏa mãn bất phương trình x – y ≥ – 3.

Đường thẳng d₃ đi qua hai điểm B(9; 3) và C(4; – 2) song song với đường thẳng d₂ có phương trình là: x – y = c.

Vì đường thẳng này đi qua B(9; 3) nên ta có: 9 – 3 = c hay c = 6.

Khi đó phương trình d₃ là x – y = 6.

Ta thấy điểm O(0; 0) có 0 – 0 = 0 < 3 thuộc miền nghiệm nên điểm O thỏa mãn bất phương trình x – y ≤ 3 (3).

Đường thẳng d₁ đi qua hai điểm C(4; – 2) và D(– 5; – 2) song song với trục hoành có phương trình y = – 2.

Ta thấy điểm O thuộc miền nghiệm có 0 > – 2 nên điểm O thỏa mãn bất phương trình y ≥ – 2 (4)

Từ (1), (2), (3) và (4) miền nghiệm của tứ giác ABCD biểu diễn cho hệ bất phương trình:

$\left\{\begin{array}{l}y\le 3\\ y\ge -2\\ x-y\ge -3\\ x-y\le 6\end{array}\right.$.

Bài 17 trang 30 SBT Toán 10 Tập 1:

a) Biểu diễn miền nghiệm của hệ bất phương trình: $\left\{\begin{array}{l}x+y\le 5\\ 3x+2y\le 12\\ x\ge 1\\ y\ge 0\end{array}\right.$.

b) Tìm x, y là nghiệm của hệ bất phương trình (III) sao cho F = 3x + 7y đạt giá trị lớn nhất, giá trị nhỏ nhất.

Lời giải:

a) Ta vẽ bốn đường thẳng:

d₁: x + y = 5 là đường thẳng đi qua hai điểm có tọa độ (0; 5) và (5; 0);

d₂: 3x + 2y = 12 là đường thẳng đi qua hai điểm có tọa độ (4; 0) và (0; 6);

d₃: x = 1 là đường thẳng song song với trục tung và đi qua điểm (1; 0);

d₄: y = 0 là trục hoành.

Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.

Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với A(1; 0), B(1; 4), C(2; 3) và D(4; 0) như hình vẽ sau:

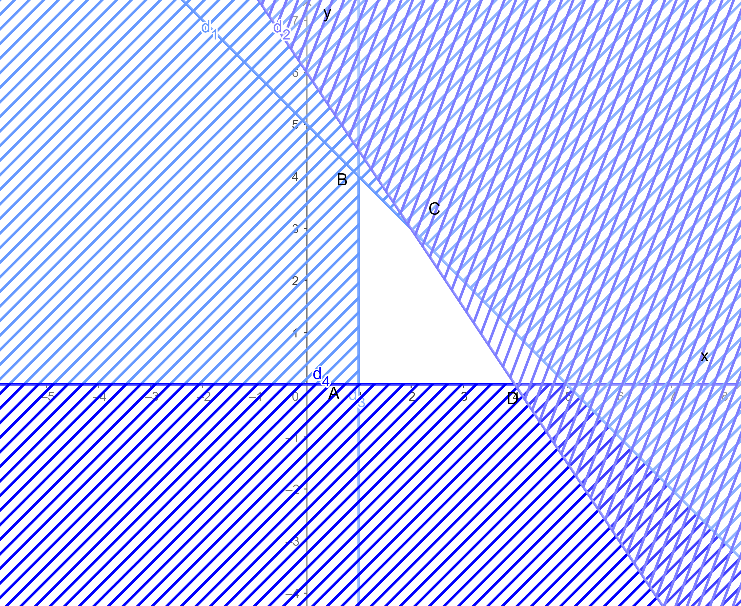
b) Ta có biểu thức F = 3x + 7y đạt giá trị lớn nhất, giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.

Tại A(1; 0) với x = 1 và y = 0 thì F = 3.1 + 7.0 = 3;

Tại B(1; 4) với x = 1 và y = 4 thì F = 3.1 + 7.4 = 31;

Tại C(2; 3) với x = 2 và y = 3 thì F = 3.2 + 7.3 = 27;

Tại D(4; 0) với x = 4 và y = 0 thì F = 3.4 + 7.0 = 12.

Vậy giá trị lớn nhất của F là 31 khi x = 1 và y = 4, giá trị nhỏ nhất của F là 3 khi x = 1 và y = 0 .

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Giải SBT Toán 10 trang 29 Tập 1

Giải SBT Toán 10 trang 31 Tập 1