50 bài tập về Diện tích hình tròn, diện tích hình quạt tròn (có đáp án 2024) - Toán 9

Diện tích hình tròn, diện tích hình quạt tròn và cách giải bài tập - Toán lớp 9

I. Lý thuyết

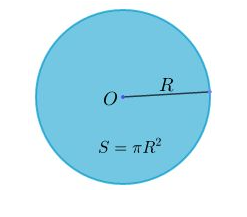
1. Công thức tính diện tích hình tròn

Diện tích S của một hình tròn bán kính R được tính theo công thức

$S=\pi R^2$(đơn vị diện tích)

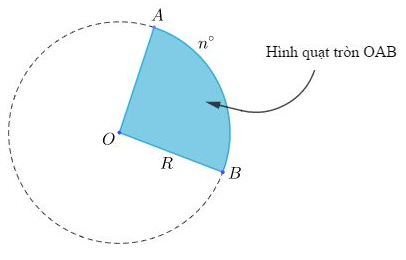
2. Công thức tính diện tích hình quạt tròn

Diện tích hình quạt tròn bán kính R, cung $n°$được tính theo công thức:

$S=\frac{\pi R^2.n}{360}$ hay $S=\frac{lR}{2}$(đơn vị diện tích)

(với l là độ dài cung $n°$của hình quạt tròn).

II. Các dạng bài tập

Dạng 1: Tính diện tích hình tròn, hình quạt tròn

Phương pháp giải: Áp dụng công thức tính diện tích hình tròn, diện tích hình quạt tròn.

Ví dụ 1: Điền vào ô trống bảng sau (làm tròn đến chữ số thập phân thứ nhất).

Bán kính đường tròn	Độ dài đường tròn	Diện tích hình tròn	Số đo của cung tròn $n°$	Diện tích hình quạt tròn cung $n°$
	12cm		$45°$
2cm				$10,5c{m}^2$
		$40c{m}^2$		$10c{m}^2$

Lời giải:

+ Độ dài đường tròn là 12cm nên C = 12cm. Bán kính đường tròn là:

$R=\frac{C}{2.\pi }=\frac{12}{2.\pi }=1,91$cm.

Diện tích hình tròn bán kính 1,91cm là: $S=R^2.\pi =1,{91}^2.\pi =11,46c{m}^2$.

Diện tích hình quạt tròn cung $45°$là: $S^{\text{'}}=\frac{\pi R^2.n}{360}=\frac{\pi .1,{91}^2.45}{360}=1,43c{m}^2$.

+ Bán kính đường tròn là 2 nên độ dài đường tròn là $C=2\pi .R=2.\pi .2=12,57cm$.

Diện tích hình tròn là: $S=R^2.\pi =2^2.\pi =12,57c{m}^2$

Vì diện tích hình quạt tròn là 10,5$c{m}^2$nên số đo của cung tròn là:

$n=\frac{360.S^{\text{'}}}{\pi R^2}=\frac{360.10,5}{12,57}=300°$.

+ Vì diện tích hình tròn là $40c{m}^2$ nên bán kính đường tròn là:

$R=\sqrt{\frac{S}{\pi }}=\sqrt{\frac{40}{\pi }}=3,57cm$.

Chu vi cung tròn là: $C=2\pi .R=2.\pi .3,57=22,42cm$

Vì diện tích hình quạt tròn bằng $\frac{1}{4}$diện tích hình tròn nên số đo cung tròn đó là $90°$.

Ta có bảng sau:

Bán kính đường tròn	Độ dài đường tròn	Diện tích hình tròn	Số đo của cung tròn $n°$	Diện tích hình quạt tròn cung $n°$
1,91cm	12cm	11,46$c{m}^2$	$45°$	$1,43c{m}^2$
2cm	12,57cm	$12,57c{m}^2$	$300°$	$10,5c{m}^2$
3,57cm	22,42cm	$40c{m}^2$	$90°$	$10c{m}^2$

Ví dụ 2: Cho hình vuông có cạnh 5cm nội tiếp đường tròn (O). Hãy tính độ dài đường tròn (O) và diện tích hình tròn (O).

Lời giải:

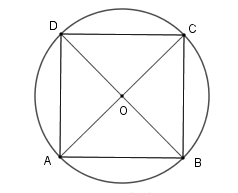
Gọi hình vuông nội tiếp đường tròn (O) là ABCD khi đó:

OA = OB = OC = OD = R => O là giao điểm của AC với BD $\Rightarrow R=\frac{AC}{2}$

Xét tam giác ABC vuông tại B ta có:

$A{C}^2=A{B}^2+B{C}^2$ (định lý Py – ta – go)

$\iff A{C}^2=5^2+5^2$

$\iff A{C}^2=25+25$

$\iff A{C}^2=50$

$\Rightarrow AC=5\sqrt{2}$ cm

Vậy bán kính đường tròn là:

$R=\frac{AC}{2}=\frac{5\sqrt{2}}{2}cm$

Chu vi đường tròn là:

$C=2\pi R=2.\pi .\frac{5\sqrt{2}}{2}=5\sqrt{2}\pi$ (cm)

Diện tích hình tròn là:

$S=\pi R^2=\pi {\left(\frac{5\sqrt{2}}{2}\right)}^2=\frac{25}{2}\pi \left(c{m}^2\right)$

Dạng 2: Tính diện tích một số hình đặc biệt liên quan đến hình tròn, hình quạt tròn

Phương pháp giải: Chia hình cần tính thành các hình nhỏ hơn có công thức tính diện tích và sử dụng công thức để tính.

Ví dụ 1: Cho (O) đường kính AB = $4\sqrt{3}$cm, điểm C thuộc (O) sao cho $\widehat{ABC}=30°$. Tính diện tích viên phân AC (viên phân là phần hình giới hạn bởi một cung tròn và dây căng cung ấy).

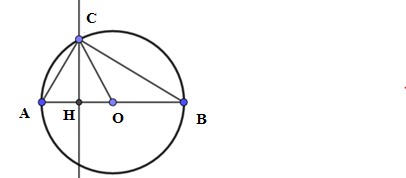
Xét đường tròn (O) có:

$\widehat{ABC}$ và $\widehat{AOC}$ là góc nội tiếp và góc ở tâm chắn cung $\stackrel{⏜}{AC}$.

$\Rightarrow \widehat{AOC}=2.\widehat{ABC}=2.30°=60°$

Diện tích hình quạt tròn AOC là:

$S_{qAOC}=\frac{\pi R^2.60}{360}=\frac{\pi R^2}{6}$

Xét tam giác AOC có:

$\widehat{AOC}=60°$

OA = OC = R
Do đó tam giác AOC là tam giác đều cạnh bằng R.

Gọi CH là đường cao của tam giác AOC

Ta có $\sin 60°=\frac{CH}{CO}$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow CH=CO.\sin 60°=\frac{\sqrt{3}}{2}R$

Diện tích tam giác AOC là:

$S_{AOC}=\frac{1}{2}CH.OA=\frac{1}{2}.\frac{\sqrt{3}}{2}R.R=\frac{\sqrt{3}}{4}{R}^2$

Diện tích viên phân AC là :

$S_{qAOC}-S_{AOC}=\frac{\pi R^2}{6}-\frac{\sqrt{3}}{4}{R}^2=\left(\frac{\pi }{6}-\frac{\sqrt{3}}{4}\right)R^2$

$=\left(\frac{\pi }{6}-\frac{\sqrt{3}}{4}\right).{\left(2\sqrt{3}\right)}^2=2\pi -3\sqrt{3}c{m}^2$

Ví dụ 2: Cho đường tròn (O; R) và một điểm M sao cho OM = 2R. Từ M vẽ các tiếp tuyến MA và MB với A, B là các tiếp điểm.

a) Tính độ dài cung nhỏ AB.

b) Tính diện tích giới hạn bởi hai tiếp tuyến AM; BM và cung nhỏ AB.

Lời giải:

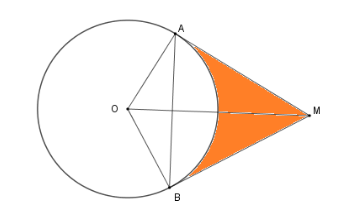
a) Vì AM là tiếp tuyến của đường tròn (O) nên AM vuông góc với OA.

Xét tam giác OAM vuông tại A ta có:

$\cos \widehat{AOM}=\frac{OA}{OM}=\frac{R}{2R}=\frac{1}{2}$ (tỉ số lượng giác trong tam giác vuông)

$\Rightarrow \widehat{AOM}=60°$. Mà OM là tia phân giác của góc $\widehat{AOB}$ (tính chất hai tiếp tuyến cắt nhau)

$\Rightarrow \widehat{AOB}=120°$.

Độ dài cung $\stackrel{⏜}{AB}$ là:

$l=\frac{\pi R.120}{180}=\frac{2\pi R}{3}$(cm)

b) Xét tam giác OAM vuông tại A ta có:

$A{M}^2+A{O}^2=O{M}^2$(định lý Py – ta – go)

$\iff A{M}^2+R^2={\left(2R\right)}^2$

$\iff A{M}^2=4R^2-R^2$

$\iff AM=\sqrt{3}R$ (đơn vị độ dài)

Diện tích tam giác OAM là:

$S=\frac{1}{2}AM.AO=\frac{1}{2}.R.\sqrt{3}R=\frac{\sqrt{3}{R}^2}{2}$(đơn vị diện tích)

Xét tam giác AOM và tam giác BOM có:

OM chung

AO = BO = R

AM = BM (tính chất hai tiếp tuyến cắt nhau)

Do đó $\Delta AOM=\Delta BOM$ (c – c – c)

$\Rightarrow S_{AOM}=S_{BOM}=\frac{\sqrt{3}{R}^2}{2}$

$S_{AMBO}=S_{AOM}+S_{BOM}=\frac{\sqrt{3}{R}^2}{2}+\frac{\sqrt{3}{R}^2}{2}=\sqrt{3}{R}^2$(đơn vị diện tích)

Diện tích quạt tròn $\stackrel{⏜}{AB}$ là:

$S_{qAB}=\frac{\pi R^2.120°}{360°}=\frac{\pi R^2}{3}$ (đơn vj diện tích)

Diện tích phần giới hạn bởi tiếp tuyến MA; MB và cung nhỏ $\stackrel{⏜}{AB}$ là:

$S=S_{AMBO}-S_{qAB}=\sqrt{3}{R}^2-\frac{\pi R^2}{3}=R^2\left(\sqrt{3}-\frac{\pi }{3}\right)$ (đơn vị diện tích)

III. Bài tập vận dụng

Bài 1: Cho hình vuông có cạnh 10cm. Tính độ dài đường tròn và diện tích hình tròn (O) nội tiếp hình vuông.

Bài 2: Một hình quạt có chu vi bằng 28cm và diện tích bằng 49$c{m}^2$. Tính bán kính hình quạt tròn đó.

Bài 3: Cho tam giác ABC nội tiếp đường tròn (O; 3cm). Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA; OC và cung nhỏ AC khi $\widehat{ABC}=60°$.

Bài 4: Cho đường tròn (I; 2cm). Vẽ bán kính IA và IB sao cho $\widehat{AIB}=120°$. Hãy tính

a) Độ dài cung nhỏ AB.

b) Diện tích hình quạt giới hạn bởi cung nhỏ AB và hai bán kính IA, IB.

Bài 5: Cho hai đường tròn đồng tâm O, bán kính lần lượt R = 5cm, r = 2cm. Lấy 2 điểm A, B thuộc (O; 2) sao cho $\widehat{AOB}=70°$. Tia OA, OB cắt đường tròn (O; R) tại D và E, lấy điểm C thuộc đường tròn (O; r).

a) Tính $\widehat{DOE};\widehat{DCE}$.

b) Tính độ dài đường tròn (O; R) và đường tròn (O; r); độ dài cung DE.

b) Tính diện tích hình tròn (O; r) và hình quạt tròn DOE.

Bài 6: Cho (O) đường kính AB = $2\sqrt{2}$cm, điểm C thuộc (O) sao cho $\widehat{ABC}=30°$. Tính diện tích hình giới hạn bởi đường tròn (O) với AB; AC.

Bà 7: Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB. Vẽ dây CD vuông góc với AB tại M. Giả sử AM = 2cm và CD = $4\sqrt{3}$cm. Tính:

a) Độ dài đường tròn (O) và diện tích hình tròn (O).

b) Độ dài cung $\stackrel{⏜}{CAD}$ và diện tích hình quạt tròn giới hạn bởi hai bán kính OC, OD và cung nhỏ $\stackrel{⏜}{CD}$.

Bài 8: Cho đường tròn (O; R), đường kính AB cố định. Gọi M là trung điểm đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung lớn CD (E khác A). Nối AE cắt CD tại K. Nối BE cắt CD tại H.

a) Chứng minh bốn điểm B, M, E, K thuộc một đường tròn.

b) Chứng minh AE.AK không đổi.

c) Tính theo R diện tích hình quạt giới hạn bởi OB, OC và cung nhỏ BC.

Bài 9: Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD = R (C thuộc cung AD). Nối AC và BD cắt nhau tại M.

a) Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc $\widehat{AMB}$không đổi.

b) Cho $\widehat{ABC}=30°$, tính độ dài cung nhỏ AC và diện tích viên phân giới hạn bởi dây cung AC và cung nhỏ AC.

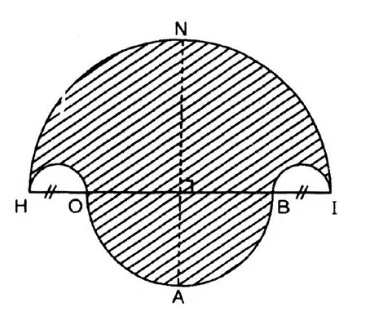
Bài 10: Cho hình vẽ là các cung tròn của các đường tròn có bán kính khác nhau được xếp nối tiếp nhau. Tính diện tích phần bị gạch trong hình vẽ biết HI = 10cm; HO = BI = 2cm.

Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác:

Bài tập về góc có đỉnh nằm trong đường tròn, góc có đỉnh nằm ngoài đường tròn và cách giải

Cung chứa góc, các bài toán về quỹ tích, dựng hình và cách giải

Tứ giác nội tiếp và cách giải bài tập

Đường tròn nội tiếp, Đường tròn ngoại tiếp và cách giải bài tập

Độ dài đường tròn, độ dài cung tròn và cách giải bài tập