50 bài tập về Cách tính diện tích tam giác bằng tỉ số lượng giác (có đáp án 2025)
Với cách giải các dạng toán về cách tính diện tích tam giác bằng tỉ số lượng giác môn Toán lớp 9 Đại số gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về cách tính diện tích tam giác bằng tỉ số lượng giác lớp 9. Mời các bạn đón xem:
Cách tính diện tích tam giác bằng tỉ số lượng giác chi tiết
A. Lý thuyết
Ôn lại các công thức tính tỉ số lượng giác của góc nhọn và công thức tính diện tích tam giác.
Cho tam giác ABC vuông tại A (như hình vẽ).
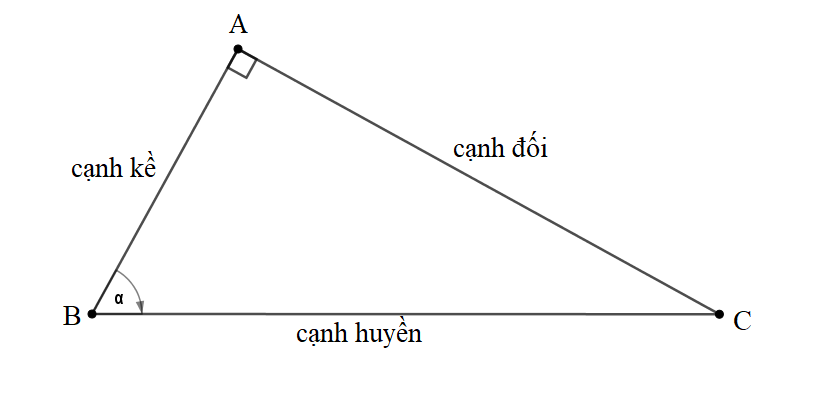
Ta có các tỉ số lượng giác của góc nhọn như sau:

Công thức tính diện tích tam giác (dùng cho tất cả tam giác):
Diện tích = 12 (đường cao) x (cạnh đáy tương ứng)
Tức là: Cho tam giác ABC có đường cao AH ứng với cạnh BC.
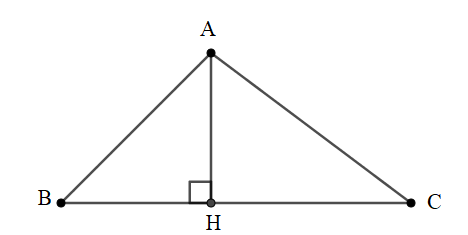
SABC=12.AH.BC
* Ngoài công thức trên, ta còn có thể sử dụng tỉ số lượng giác để tính diện tích của tam giác, quan sát ở Bài 1 phần ví dụ mịnh họa dưới đây.
B. Ví dụ minh họa
Bài 1: Cho tam giác nhọn ABC. Chứng minh rằng SABC=12.AB.AC.sin^BAC
Giải:
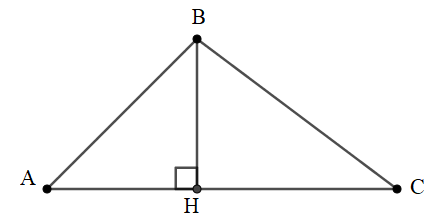
+) Vẽ tam giác nhọn ABC như hình, có đường cao BH.
+) Xét tam giác ABH vuông tại H:
Áp dụng tỉ số lượng giác của góc nhọn ta có:
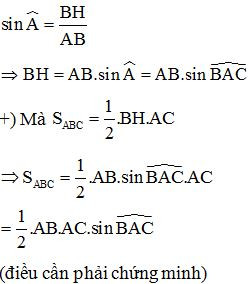
Nhận xét: Như vậy ta có thêm một cách tính diện tích tam giác nữa.
Tổng quát như sau: Diện tích của một tam giác bằng nửa tích hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.
Bài 2: Cho tam giác ABC như hình vẽ. Có ˆB=30o, AB = 5 cm, BC = 8 cm. Tính diện tích tam giác ABC.
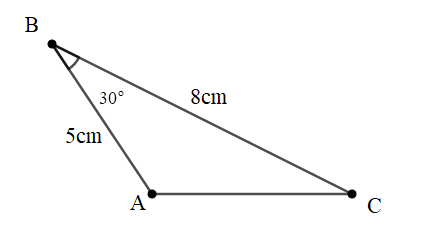
Giải:
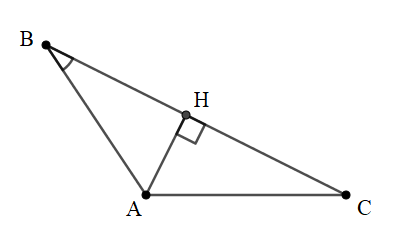
Cách 1:
+) Kẻ đường cao AH ứng với cạnh BC. Xét tam giác AHB vuông tại H:
Áp dụng tỉ số lượng giác của góc nhọn ta có:
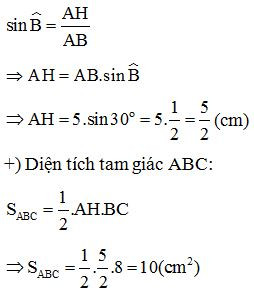
Cách 2: Ta áp dụng cách tính diện tích tam giác bằng tỉ số lượng giác của góc nhọn
Khi đó diện tích tam giác ABC là
SABC = 12AB.BC.sin^ABC=12.5.8.sin30° (cm2)
Bài 3: Cho tam giác ABC, góc A bằng , biết AB + AC = 8 cm. Tính giá trị lớn nhất của diện tích tam giác ABC.
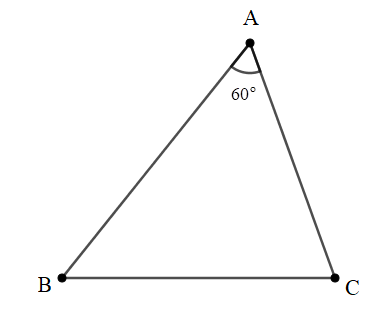
Giải:
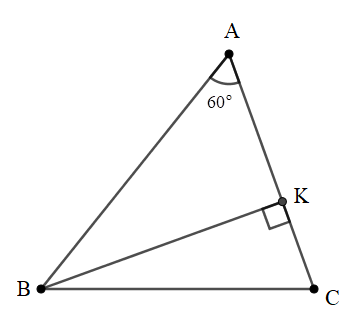
+) Kẻ đường cao BK ứng với AC. Xét tam giác BKA vuông tại K .
Áp dụng tỉ số lượng giác của góc nhọn ta có:
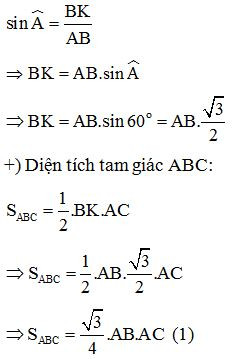
+) Áp dụng bất đẳng thức Cô-si cho hai số dương AB và AC ta có:
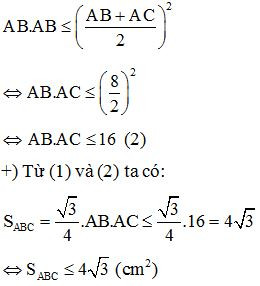
Vậy giá trị lớn nhất của diện tích tam giác ABC là .
C. Bài tập tự luyện
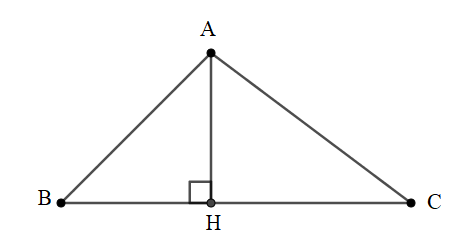
Bài 1: Cho tam giác nhọn ABC có đường cao AH ứng với cạnh BC như hình vẽ. Nhận định nào sau đây là sai ?
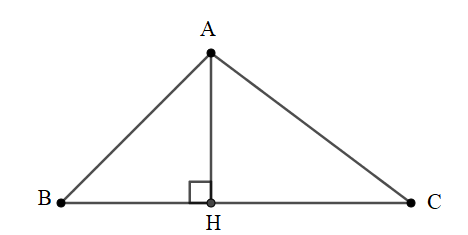
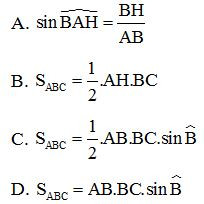
Đáp án: D.
Bài 2: Cho tam giác nhọn ABC. Chứng minh
Đáp án:
Bài 3: Cho tam giác nhọn MNP có đường cao NK ứng với cạnh MP. Chứng minh rằng:
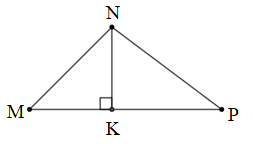
Đáp án:
Bài 4: Cho tam giác nhọn ABC . Biết AB=12cm, AC=9cm, . Tính diện tích tam giác ABC.
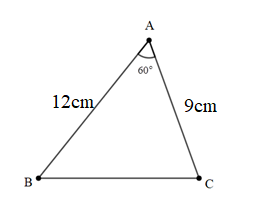
Đáp án:
Bài 5: Cho tam giác nhọn HKI. Biết , IH=10cm, IK=7cm. Tính diện tích tam giác HKI.
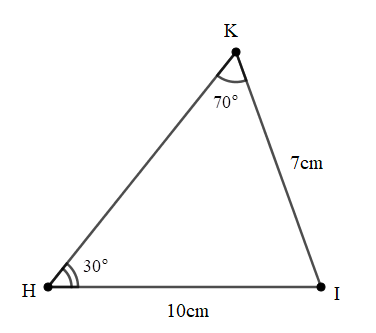
Đáp án:
Bài 6: Cho tam giác ABC như hình vẽ. Biết AB=14cm, AC=6cm, . Tính diện tích tam giác ABC.
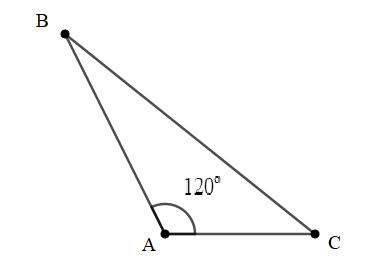
Đáp án:
Bài 7: Cho hình thoi ABCD. Biết , AB=5cm, AC=7cm. Tính diện tích hình thoi ABCD.
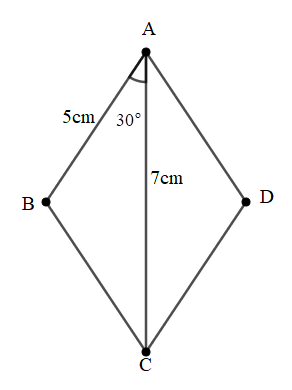
Đáp án:
Bài 8: Cho tam giác ABC, góc A bằng , đường phân giác AD. Chứng minh rằng:
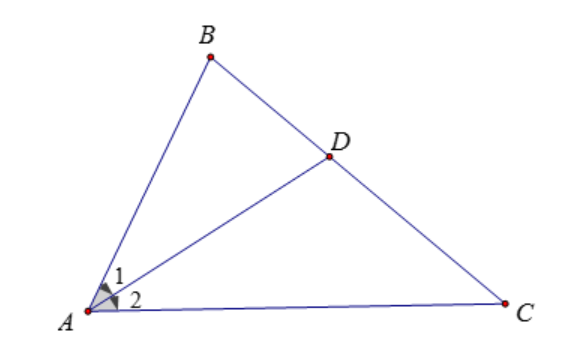
Đáp án:
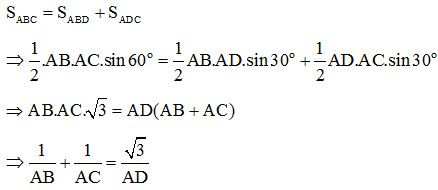
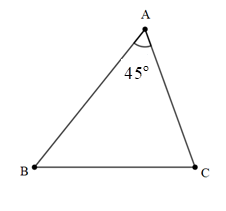
Bài 9: Cho tam giác nhọn ABC. Có , AB+AC=18(cm). Tính diện tích lớn nhất của tam giác ABC.
Đáp án:
Bài 10: Cho tam giác ABC cân tại A, AB = AC = 5 cm, góc A bằng . Trên tia đối của các tia AB và AC lần lượt lấy các điểm M và N sao cho AM + AN = 6 cm. Tính diện tích lớn nhất của tứ giác BCMN.
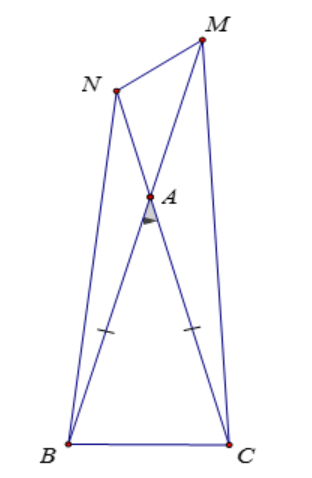
Đáp án:
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9
