Các dạng bài tập Đồ thị hàm số y = a.x^2 (có đáp án 2024) và cách giải - Toán 9

Các dạng bài tập Đồ thị hàm số y = a.x^2 và cách giải bài tập - Toán lớp 9

A. Lí thuyết

- Đồ thị của hàm số: Đồ thị của hàm số y = a$x^2$ (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol)

+) Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.

+) Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.

B. Các dạng bài tập và ví dụ minh họa

Dạng 1: Cách vẽ đồ thị của hàm số y = a$x^2$ (a ≠ 0)

Phương pháp giải:

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Lập bảng giá trị (thường từ 3 đến 4 giá trị) tương ứng giữa x và y sao cho các điểm tương ứng nằm bên phải trục Oy.

Bước 3: Vẽ trục tọa độ Oxy và đánh dấu điểm O, các điểm đã lập trong bảng giá trị và các điểm đối xứng với chúng qua trục Oy.

Bước 4: Đồ thị hàm số y = a$x^2$ (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng. Vẽ đường cong parabol đi qua các điểm đã đánh dấu ta được đồ thị hàm số y = a$x^2$ (a ≠ 0) và kết luận.

Ví dụ minh họa:

Ví dụ 1: Vẽ đồ thị hàm số y = $x^2$.

Lời giải:

Tập xác định của hàm số là: $D=ℝ$

Bảng giá trị tương ứng của x và y

x	1	2	3
y	1	4	9

Trên mặt phẳng tọa độ Oxy, lấy các điểm O(0; 0), A(1; 1), B(2; 4), C(3; 9) và A’(-1; 1), B’(-2; 4), C’(-3; 9) rồi lần lượt nối chúng theo đường cong parabol.

Ta có đồ thị hàm số y = $x^2$.

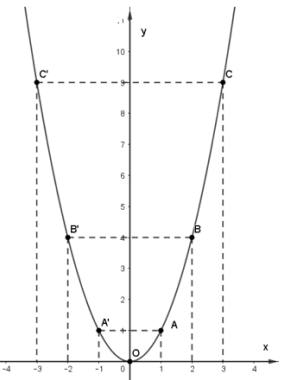
Ví dụ 2: Cho hàm số y = -$x^2$. Vẽ đồ thị hàm số y = -$x^2$

Lời giải:

Tập xác định của hàm số là: $D=ℝ$

Bảng giá trị tương ứng của x và y

x	1	2	3
y	-1	-4	-9

Trên mặt phẳng tọa độ Oxy, lấy các điểm O(0; 0), A(1; -1), B(2; -4), C(3; -9) và A’(-1; -1), B’(-2; -4), C’(-3; -9) rồi lần lượt nối chúng theo đường cong parabol.

Ta có đồ thị hàm số y = -$x^2$.

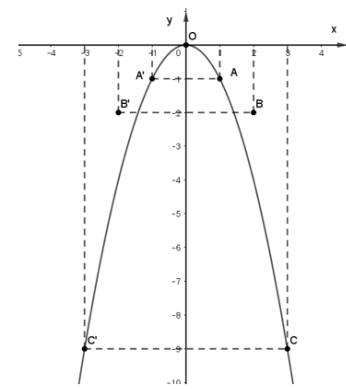
Dạng 2: Điểm thuộc, không thuộc đồ thị hàm số

Phương pháp giải:

Điểm M$\left(x_0;y_0\right)$ thuộc đồ thị hàm số y = a$x^2$ (a ≠ 0) khi và chỉ khi $a{x_0}^2=y_0$

Ví dụ minh họa:

Ví dụ 1: Trong các điểm M(1; 1), N(3; 2) và P(4; -16), những điểm nào thuộc đồ thị hàm số y = -$x^2$

Lời giải:

Những điểm thuộc đồ thị hàm số y = - $x^2$ phải có tọa độ (x; y) tương ứng sao cho y = - $x^2$.

Xét điểm M(1; 1) ta có: $-1^2=-1\ne 1$. Do đó, M không thuộc đồ thị hàm số y = - $x^2$

Xét điểm N(3; 2) ta có: $-3^2=-9\ne 2$. Do đó, N không thuộc đồ thị hàm số y = - $x^2$

Xét điểm P(4; -16) ta có: $-4^2=-16$. Do đó, P thuộc đồ thị hàm số y = - $x^2$

Vậy trong các điểm trên chỉ có điểm P thuộc đồ thị hàm số y = - $x^2$

Ví dụ 2: Điểm D(1; 3) có thuộc đồ thị hàm số $y=-3x^2$ không ? Vì sao ?

Lời giải:

Xét điểm D(1; 3) ta có: $-{3.1}^2=-3.1=-3\ne 3$

Do đó, điểm D(1; 3) không thuộc đồ thị hàm số $y=-3x^2$

Dạng 3: Các bài toán về đường thẳng và parabol

Phương pháp giải:

- Cho đường thẳng y = a’x + b và parabol y = a$x^2$ (a khác 0). Hoành độ giao điểm của chúng là nghiệm của phương trình: a’x + b = a$x^2$ (*). Giải phương trình ta tìm được hoành độ giao điểm, từ đó tìm được tọa độ giao điểm. Tọa độ giao điểm vừa là nghiệm của phương trình đường thẳng, vừa là nghiệm của phương trình parabol.

- Số nghiệm của phương trình (*) là số giao điểm của đường thẳng và parabol, ngược lại, số giao điểm của đường thẳng và parabol là số nghiệm của phương trình hoành độ giao điểm.

Ví dụ minh họa:

Ví dụ 1: Cho đường thẳng d: y = 3x và parabol y = 6$x^2$. Tìm tọa độ giao điểm của đường thẳng d và parabol.

Lời giải:

Ta có phương trình hoành độ giao điểm:

3x = 6$x^2$

$\iff 6x^2-3x=0$

$\iff 3x(2x-1)=0$

$\iff \left[\begin{array}{l}3x=0\\ 2x-1=0\end{array}\right.$

$\iff \left[\begin{array}{l}x=0\\ x=\frac{1}{2}\end{array}\right.$

Với x = 0, ta có: y = 3.0 = 0, do đó, giao điểm là A(0; 0)

Với x = $\frac{1}{2}$, ta có: $y=3.\frac{1}{2}=\frac{3}{2}$, do đó, giao điểm là B$\left(\frac{1}{2};\frac{3}{2}\right)$

Vậy đường thẳng d và parabol có 2 giao điểm là A(0; 0) và B$\left(\frac{1}{2};\frac{3}{2}\right)$

Ví dụ 2: Cho đồ thị của hàm số y = $x^2$ và đường thẳng d: y = (m + 3)x như hình vẽ.

a) Dựa vào đồ thị, biện luận số nghiệm của phương trình $x^2-(m+3)x=0$

b) Biết một giao điểm có hoành độ bằng 3. Tìm tham số m.

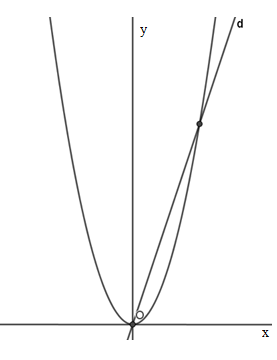
Lời giải:

a)

Ta có phương trình hoành độ giao điểm của parabol y = $x^2$ và đường thẳng d: y = (m + 3)x là:

$x^2=(m+3)x$

$\iff x^2-(m+3)x=0$

Dựa vào đồ thị, ta thấy parabol y = $x^2$ và đường thẳng d: y = (m + 3)x có hai giao điểm, do đó, phương trình hoành độ giao điểm của chúng có 2 nghiệm phân biệt hay phương trình $x^2-(m+3)x=0$ có hai nghiệm phân biệt.

b)

Ta có phương trình hoành độ giao điểm của parabol y = $x^2$ và đường thẳng d: y = (m + 3)x là:

$x^2=(m+3)x$

$\iff x^2-(m+3)x=0$

Mà x = 3 là hoành độ của một giao điểm nên ta có:

$3^2-(m+3).3=0$

$\iff 9-3m-9=0$

$\iff -3m=0$

$\iff m=0$

Vậy m = 0

C. Bài tập tự luyện

Bài 1: Vẽ đồ thị hàm số y = -4$x^2$

Bài 2: Vẽ đồ thị hàm số y = 5$x^2$

Bài 3: Tìm tọa độ giao điểm của parabol y = -2$x^2$ và đường thẳng y = x.

Bài 4: Tìm tọa độ giao điểm của parabol y = $x^2$ và đường thẳng y = 2x – 1.

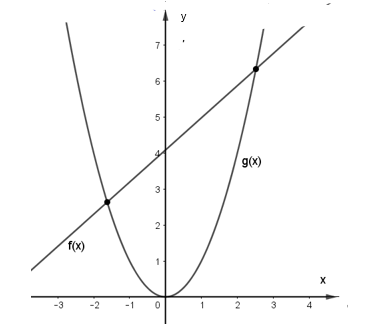
Bài 5: Cho đồ thị của đường thẳng d: y = f(x) và parabol y = g(x) như hình vẽ. Hãy cho biết, phương trình f(x) – g(x) = 0 có bao nhiêu nghiệm ?

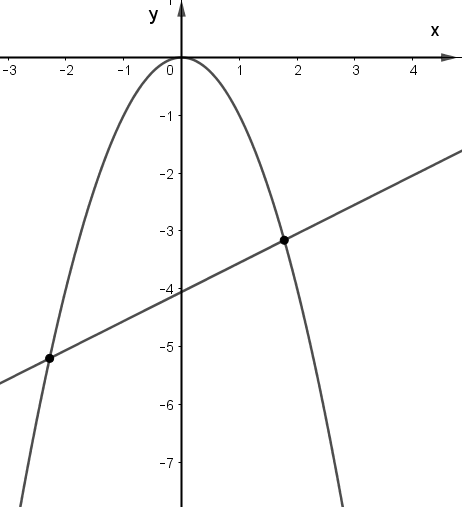
Bài 6: Cho đồ thị của đường thẳng d: y = f(x) và parabol y = g(x) như hình vẽ. Hãy cho biết, phương trình $f^2\left(x\right)-f\left(x\right).g\left(x\right)=0$ có bao nhiêu nghiệm ?

Bài 7: Cho hàm số y = m$x^2$ có đồ thị là parabol (P). Tìm giá trị của m biết rằng parabol (P) cắt đường thẳng (d): y = x – 3 tại điểm có hoành độ bằng 5.

Bài 8: Cho hàm số y = -2$x^2$. Trong các điểm A(1; -2), B(3; -9), C(-2; -4), những điểm nào thuộc đồ thị hàm số y = -2$x^2$.

Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác:

Các dạng bài tập Hàm số y = a.x^2 và cách giải bài tập

Phương trình bậc hai một ẩn và cách giải bài tập

Hệ thức Vi-ét và ứng dụng và cách giải bài tập

Phương trình quy về phương trình bậc hai một ẩn và cách giải bài tập

Giải bài toán bằng cách lập phương trình và cách giải bài tập