Nội dung bài viết

    Xem thêm

    Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm K, trên cạnh AC lấy điểm H sao cho BK = CH

    Lời giải Bài 6 trang 62 vở thực hành Toán 8 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Vở thực hành Toán 8.

    1 412 11/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Vở thực hành Toán 8 Bài 14: Hình thoi và hình vuông

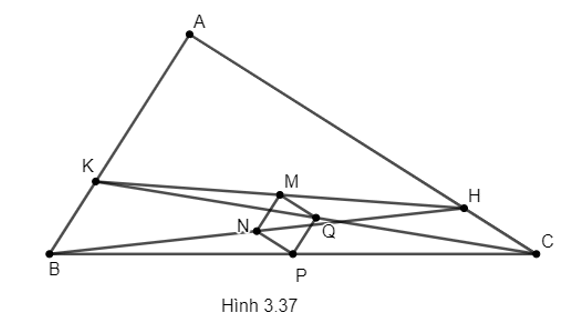
    Bài 6 trang 62 vở thực hành Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm K, trên cạnh AC lấy điểm H sao cho BK = CH. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh KH, BH, BC, CK. Chứng minh rằng MNPQ là hình vuông.

    Lời giải:

    Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm K

    (H.3.37). Vì MK = MH, NB = NH ⇒ MN là đường trung bình trong tam giác HKB.

    ⇒ MN // KB và MN = 12KB (1)

    Chứng minh tương tự, ta có:

    PQ // KB và PQ = 12KB (2)

    NP // CH và NP = 12CH (3)

    Từ (1) và (2), ta có MN // PQ và MN = PQ ⇒ MNPQ là hình bình hành (4)

    Ta có BK = CH (giả thiết). (5)

    Từ (1), (3) và (5), ta có MN = NP ⇒ MNPQ là hình thoi (6)

    Vì ∆ABC vuông tại A (giả thiết) ⇒ BK ⊥ CH, mà NP // CH, MN // KB (chứng minh trên).

    ⇒ MN ⊥ NP (7).

    Từ (6) và (7), ta có MNPQ là hình thoi có một góc vuông nên nó là hình chữ nhật.

    Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Câu 1 trang 60 vở thực hành Toán 8 Tập 1: Điền cụm từ thích hợp vào chỗ trống a) Trong hình thoi ............................ vuông góc với nhau và là ............. các góc của hình thoi...

    Câu 2 trang 60 vở thực hành Toán 8 Tập 1: Điền cụm từ thích hợp vào chỗ trống a) Nếu ABCD là một hình vuông thì ta có: AC = ......, AC vuông góc với ....

    Bài 1 trang 60 vở thực hành Toán 8 Tập 1: Tìm các hình thoi và hình vuông trong Hình 3.32...

    Bài 2 trang 61 vở thực hành Toán 8 Tập 1: Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC...

    Bài 3 trang 61 vở thực hành Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của hình thoi...

    Bài 4 trang 62 vở thực hành Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật...

    Bài 5 trang 62 vở thực hành Toán 8 Tập 1: Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng MA ⊥ MD...

    Bài 6 trang 62 vở thực hành Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm K, trên cạnh AC lấy điểm H sao cho BK = CH...

    Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác: 

    Bài 13: Hình chữ nhật

    Luyện tập chung trang 63

    Bài tập cuối chương 3

    Bài 15: Định lí Thalès trong tam giác

    Bài 16: Đường trung bình của tam giác

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 412 11/08/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: