Nội dung bài viết

    Xem thêm

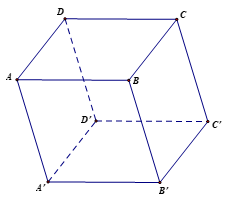
    Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: a) vecto AB + vecto B'C' + vetco DD' = vecto AC'

    Lời giải Bài 1 trang 50 Toán 12 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

    1 566 11/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Chân trời sáng tạo Bài 1: Vectơ và các phép toán trong không gian

    Bài 1 trang 50 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:

    a) AB→+B'C'→+DD'→=AC'→;

    b) DB'→+D'D→+BD'→=BB'→;

    c) AC→+BA'→+DB→+C'D→=0→.

    Lời giải:

    Bài 1 trang 50 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    a) AB→+B'C'→+DD'→=AC'→

    Do ABCD.A'B'C'D' là hình hộp nên các mặt của nó là hình bình hành.

    Khi đó DD'→=AA'→; B'C'→=AD→=BC→.

    Do đó AB→+B'C'→+DD'→=AB→+AD→+AA'→=AC'→ (theo quy tắc hình hộp).

    b) DB'→+D'D→+BD'→=BB'→

    Có DB'→+D'D→+BD'→

    =DB→+BB'→+D'B→+BD→+BD'→

    =DB→+BD→+BB'→+D'B→+BD'→

    = BB'→

    Vì DB→+BD→=0→;D'B→+BD'→=0→.

    c) AC→+BA'→+DB→+C'D→=0→

    Vì AD // B'C' và AD = B'C' (do cùng song song và bằng BC).

    Do đó ADC'B' là hình bình hành.

    Suy ra AB'→ và C'D→ là hai vectơ đối nhau. Do đó AB'→+C'D→=0→.

    Tương tự DA'B'C là hình bình hành.

    Suy ra B'C→ và DA'→ là hai vectơ đối nhau. Do đó B'C→+DA'→=0→.

    AC→+BA'→+DB→+C'D→

    =AB'→+B'C→+DB→+BA'→+C'D→

    =AB'→+B'C→+DA'→+C'D→

    =AB'→+C'D→+B'C→+DA'→=0→

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Hoạt động khởi động trang 41 Toán 12 Tập 1: Trong không gian, làm thế nào để biểu diễn độ dịch chuyển tín hiệu vô tuyến từ máy bay đến trạm kiểm soát trên mặt đất.

    Hoạt động khám phá 1 trang 41 Toán 12 Tập 1: Nhắc lại định nghĩa vectơ trong mặt phẳng. Có thể định nghĩa vectơ trong không gian như đã định nghĩa vectơ trong mặt phẳng không?

    Thực hành 1 trang 42 Toán 12 Tập 1: Trong hoạt động khởi động, tìm vectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A của máy bay đến vị trí S của trạm kiểm soát.

    Thực hành 2 trang 42 Toán 12 Tập 1: Cho hình chóp tứ giác đều S.ABCD. a) Chỉ ra các vectơ có điểm đầu là S và điểm cuối là các đỉnh của đa giác đáy...

    Vận dụng 1 trang 43 Toán 12 Tập 1: Trong Hình 4, cho biết ba vectơ F1→,F2→,F3→ biểu diễn lực căng của các sợi dây cáp AB, AC, AD tác dụng lên vật nặng...

    Hoạt động khám phá 2 trang 43 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' (Hình 5).a) Trong mặt phẳng (ABCD), tìm vectơ tổng AB→+BC→ ...

    Hoạt động khám phá 3 trang 44 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. a) Tìm các vectơ tổng AB→+AD→,AC→+AA'→ ...

    Thực hành 3 trang 45 Toán 12 Tập 1: Cho hình hộp ABCD.EFGH. Tìm các vectơ: a) DA→+DC→+DH→ ; b) HE→+GC→+AB→ .

    Hoạt động khám phá 4 trang 45 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' a) Trong mặt phẳng (ABCD), tìm vectơ hiệu AB→−AD→ ...

    Thực hành 4 trang 46 Toán 12 Tập 1: Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Tìm các vectơ: a) BM→+AC→+ND→ ; b) AD→−AM→+NC→ .

    Thực hành 5 trang 46 Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây...

    Vận dụng 2 trang 46 Toán 12 Tập 1: Ba lực F1→,F2→,F3→ cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2 N; 3N; 4 N (Hình 17)...

    Hoạt động khám phá 5 trang 46 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' có AC' và A'C cắt nhau tại O (Hình 18)...

    Thực hành 6 trang 47 Toán 12 Tập 1: Cho hình lăng trụ ABC.A'B'C' có M là trung điểm của BB' (Hình 20). Đặt CA→=a→, CB→=b→, CC'→=c→. Chứng minh rằng AM→=b→−a→+12c→.

    Vận dụng 3 trang 48 Toán 12 Tập 1: Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp...

    Hoạt động khám phá 6 trang 48 Toán 12 Tập 1: a) Nhắc lại định nghĩa góc giữa hai vectơ u→ và v→ trong mặt phẳng...

    Thực hành 7 trang 49 Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D'. Xác định góc AC→,B'D'→, A'A→,CB'→.

    Hoạt động khám phá 7 trang 49 Toán 12 Tập 1: Trong không gian, cho u→ và v→ thỏa mãn u→=2,v→=3. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho AB→=u→,AC→=v→...

    Thực hành 8 trang 50 Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1.

    a) Tính các tích vô hướng: AB→.A'C'→ , AB→.CC'→ ...

    Vận dụng 4 trang 50 Toán 12 Tập 1: Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5 m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là 30° (Hình 27)...

    Bài 1 trang 50 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: a) AB→+B'C'→+DD'→=AC'→; b) DB'→+D'D→+BD'→=BB'→;...

    Bài 2 trang 51 Toán 12 Tập 1: Cho hình bình hành ABCD. Gọi S là một điểm không thuộc mặt phẳng chứa hình bình hành. Chứng minh rằng SA→+SC→=SB→+SD→.

    Bài 3 trang 51 Toán 12 Tập 1: Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với 3 cạnh và cùng có cường độ là 5 N. Tính cường độ của hợp lực.

    Bài 4 trang 51 Toán 12 Tập 1: Cho hình chóp S.ABCD. Gọi I là trọng tâm của tam giác ABC và J là trọng tâm tam giác ADC. Chứng minh rằng 2SA→+SB→+2SC→+SD→=3SI+SJ→.

    Bài 5 trang 51 Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C' có AA'→=a→,AB→=b→,AC→=c→. Chứng minh rằng B'C→=c→−a→−b→ và BC'→=a→−b→+c→.

    Bài 6 trang 51 Toán 12 Tập 1: Nếu một vật có khối lượng m (kg) thì lực hấp dẫn P→ của Trái Đất tác dụng lên vật được xác định theo công thức P→=mg→, trong đó g→ là gia tốc rơi tự do...

    Bài 7 trang 51 Toán 12 Tập 1: Trong điện trường đều, lực tĩnh điện F→(đơn vị: N) tác dụng lên điện tích điểm có điện tích q (đơn vị: C) được tính theo công thức F→=q.E→...

    Bài 8 trang 51 Toán 12 Tập 1: Một lực tĩnh điện F→ tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MPN (Hình 30)...

     

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài tập cuối chương 1 trang 37

    Bài 2: Toạ độ của vectơ trong không gian

    Bài 3: Biểu thức toạ độ của các phép toán vectơ

    Bài tập cuối chương 2 trang 65

    Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 566 11/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: