Nội dung bài viết

    Xem thêm

    Viết phương trình tiếp tuyến của đường cong y = x3

    Với giải Bài 5 trang 156 SGK Toán lớp 11 Đại số và giải tích được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

    1 5,125 18/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 11 Bài 1: Định nghĩa và ý nghĩa của đạo hàm

    Bài tập 5 trang 156 SGK Toán lớp 11 Đại số: Viết phương trình tiếp tuyến của đường cong y = x3:

    a) Tại điểm (–1; –1).

    b) Tại điểm có hoành độ bằng 2.

    c) Biết hệ số góc của tiếp tuyến bằng 3.

    Lời giải:

    a) Ta có:

    limx→x0f(x)−fx0x−x0=limx→x0x3−x03x−x0=limx→x0x2+x.x0+x02=x02+x0.x0+x02=3x02

    ⇒y'x0=3x02

    Ta có: y′(–1) = 3

    Vậy phương trình tiếp tuyến tại điểm (–1; –1) là: y = 3(x + 1) – 1 = 3x + 2

    b) Ta có:

    y′(2) = 3.22 = 12

    y(2) = 23 = 8

    Vậy phương trình tiếp tuyến tại điểm có hoành độ bằng 2 là:

    y = 12(x – 2) + 8 = 12x – 16.

    c) Gọi x0 là hoành độ tiếp điểm. Ta có:

    y′(x0) = 3 ⇔ 3x02 = 3 ⇔ x02 = 1 ⇔x0=±1

    Với x0 = 1 ta có y(1) = 1, phương trình tiếp tuyến là: y = 3(x − 1) + 1 = 3x – 2

    Với x0 = −1 ta có y(−1) = −1, phương trình tiếp tuyến là: y = 3(x + 1) – 1 = 3x + 2

    *Phương pháp giải:

    Dạng 1. Viết phương trình tiếp tuyến của đường tròn tại một điểm thuộc đường tròn

    - Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm M(x0;y0) thuộc đường tròn (C).

    + Nếu phương trình đường tròn có dạng x2+y2−2ax−2by+c=0 thì phương trình tiếp tuyến là: xx0+yy0−a(x+x0)−b(y+y0)+c=0.

    + Nếu phương trình đường tròn có dạng (x−a)2+(y−b)2=R2 thì phương trình tiếp tuyến là: (x−a)(x0−a)+(y−b)(y0−b)=R2

    *Lý thuyết:

    Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính tại điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.

    - Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.

    - Từ một điểm trên đường tròn ta có duy nhất một tiếp tuyến đi qua điểm đó. Từ một điểm ngoài đường tròn, ta có hai tiếp tuyến với đường tròn đi qua điểm đó.

    II. Viết phương trình tiếp tuyến của đường tròn

    Dạng 1. Viết phương trình tiếp tuyến của đường tròn tại một điểm thuộc đường tròn

    - Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm M(x0;y0) thuộc đường tròn (C).

    + Nếu phương trình đường tròn có dạng x2+y2−2ax−2by+c=0 thì phương trình tiếp tuyến là: xx0+yy0−a(x+x0)−b(y+y0)+c=0.

    + Nếu phương trình đường tròn có dạng (x−a)2+(y−b)2=R2 thì phương trình tiếp tuyến là: (x−a)(x0−a)+(y−b)(y0−b)=R2

    Dạng 2. Viết phương trình tiếp tuyến của đường tròn tại một điểm ngoài đường tròn

    - Cho đường tròn (C): (x−a)2+(y−b)2=R2 hoặc x2+y2−2ax−2by+c=0. Điểm N(x0;y0) nằm ngoài đường tròn (C).

    + Viết phương trình của đường thẳng đi qua điểm N:

    y−y0=m(x−x0)⇔mx−y−mx0+y0=0 (1)

    + Có d(I,d)=R ta tính được m thay m vào phương trình (1) ta được phương trình tiếp tuyến. Ta luôn tìm được hai đường tiếp tuyến.

    Dạng 3. Viết phương trình tiếp tuyến song song với phương cho sẵn có hệ số góc k

    Phương trình đường thẳng (d) có dạng y = kx + m (m chưa biết)

    kx - y + m = 0

    Cho khoảng cách từ tâm I đến (d) = R ta tìm được m

    Ta luôn tìm được 2 tiếp tuyến

    Xem thêm

    Phương trình tiếp tuyến của đường tròn (lý thuyết, công thức và cách giải các dạng bài tập)

    50 bài tập về tiếp tuyến (có đáp án 2024) và cách giải

    Xem thêm lời giải bài tập Toán lớp 11 hay, chi tiết khác:

    Hoạt động 1 trang 146 SGK Toán lớp 11 Đại số: Một đoàn tàu chuyển động thẳng khởi hành từ một ga...

    Hoạt động 2 trang 149 SGK Toán lớp 11 Đại số: Cho hàm số y = x2. Hãy tính y′(x0) bằng định nghĩa...

    Hoạt động 3 trang 150 SGK Toán lớp 11 Đại số: a) Vẽ đồ thị của hàm số ...

    Hoạt động 4 trang 152 SGK Toán lớp 11 Đại số: Viết phương trình đường thẳng đi qua M0(x0; y0) và có hệ số góc k...

    Hoạt động 5 trang 152 SGK Toán lớp 11 Đại số: Cho hàm số y = –x2 + 3x – 2. Tính y′(2) bằng định nghĩa...

    Hoạt động 6 trang 153 SGK Toán lớp 11 Đại số: Bằng định nghĩa, hãy tính đạo hàm của các hàm số...

    Bài tập 1 trang 156 SGK Toán lớp 11 Đại số: Tìm số gia của hàm số f(x) = x3, biết rằng...

    Bài tập 2 trang 156 SGK Toán lớp 11 Đại số: Tính Δy và 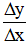Giải bài 2 trang 156 sgk Đại Số 11 | Để học tốt Toán 11 của các hàm số sau theo x và Δx...

    Bài tập 3 trang 156 SGK Toán lớp 11 Đại số: Tính (bằng định nghĩa) đạo hàm của mỗi hàm số sau tại các điểm đã chỉ ra...

    Bài tập 4 trang 156 SGK Toán lớp 11 Đại số: Chứng minh rằng hàm số...

    Bài tập 6 trang 156 SGK Toán lớp 11 Đại số: Viết phương trình tiếp tuyến của đường hypebol...

    Bài tập 7 trang 157 SGK Toán lớp 11 Đại số: Một vật rơi tự do theo phương trình...

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 5,125 18/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: