Nội dung bài viết

    Xem thêm

    Vẽ đồ thị các hàm số bậc ba sau: a) y = x^3; b) y = x^3 – 3x; c) y = −x^3 + 3x; d) y = x^3 – 3x + 2

    Lời giải Thực hành 1 trang 89 Toán 12 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

    1 118 17/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Chân trời sáng tạo Bài 1: Vẽ đồ thị hàm số bằng phần mềm Geogebra

    Thực hành 1 trang 89 Toán 12 Tập 1: Vẽ đồ thị các hàm số bậc ba sau:

    a) y = x3;       b) y = x3 – 3x;

    c) y = −x3 + 3x;    d) y = x3 – 3x + 2.

    Lời giải:

    a) y = x3

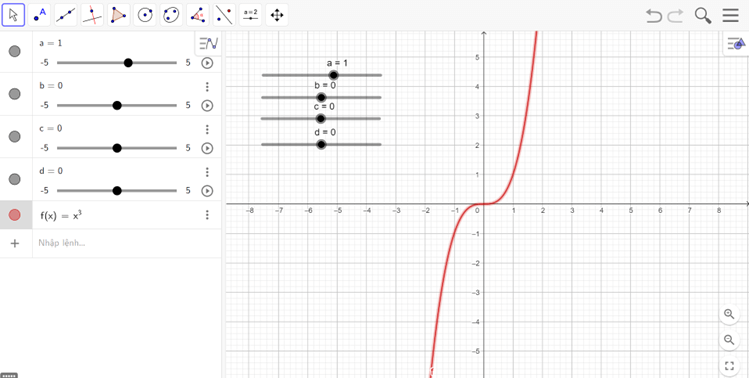
    - Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12 và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

    Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    - Nhập hàm số y = x3 vào vùng nhập lệnh.

    - Ta được đồ thị như hình vẽ

    Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    - Nhận xét:

    Hàm số đồng biến trên khoảng (0; +∞) và nghịch biến trên khoảng (−∞; 0).

    Hàm số đã cho không có cực trị.

    Đồ thị có tâm đối xứng là (0; 0).

    b) y = x3 – 3x

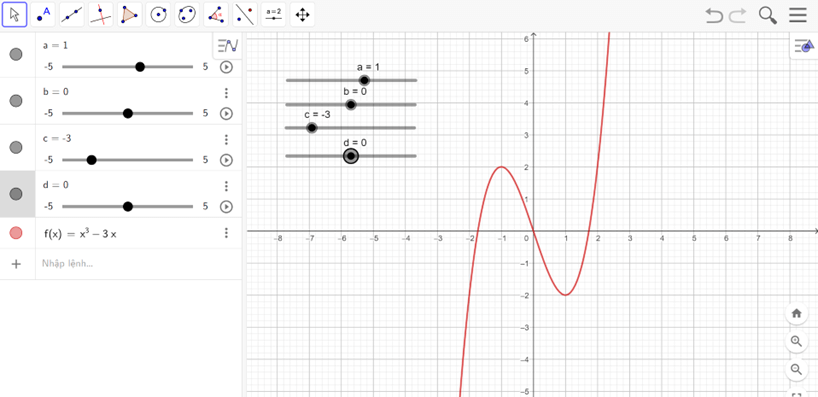
    - Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12 và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

    Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    - Nhập hàm số y = x3 – 3x vào vùng nhập lệnh.

    - Ta được đồ thị như hình vẽ

    Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    Nhận xét:

    Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).

    Hàm số nghịch biến trên khoảng (−1; 1).

    Điểm cực đại là (−1; 2), điểm cực tiểu là (1; −2).

    Đồ thị hàm số có tâm đối xứng là (0; 0).

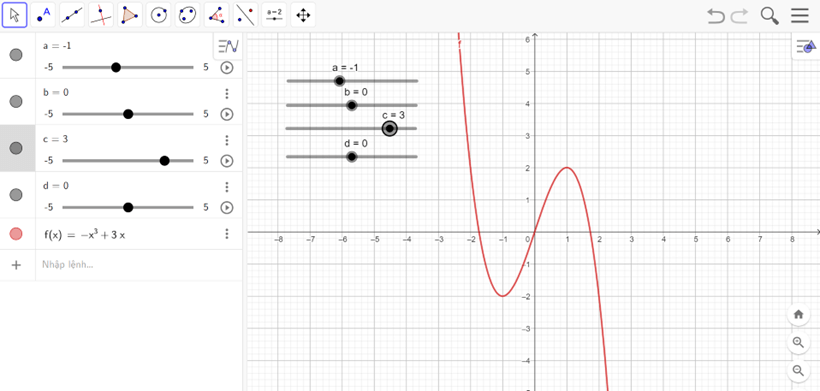
    c) y = −x3 + 3x

    - Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12 và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

    Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    - Nhập hàm số y = −x3 + 3x vào vùng nhập lệnh.

    - Ta được đồ thị như hình vẽ

    Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    Nhận xét:

    Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; +∞).

    Hàm số đồng biến trên khoảng (−1; 1).

    Điểm cực đại là (1; 2), điểm cực tiểu là (−1; −2).

    Đồ thị hàm số có tâm đối xứng là (0; 0).

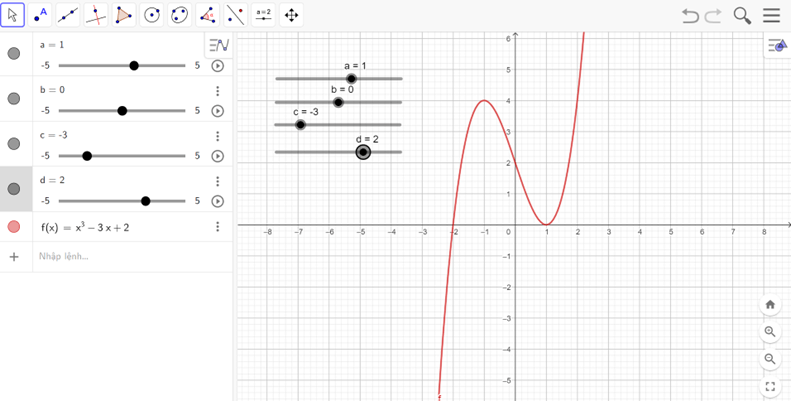
    d) y = x3 – 3x + 2

    - Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12 và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

    Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    - Nhập hàm số y = x3 – 3x + 2 vào vùng nhập lệnh.

    - Ta được đồ thị như hình vẽ

    Thực hành 1 trang 89 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    Nhận xét:

    Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).

    Hàm số nghịch biến trên khoảng (−1; 1).

    Điểm cực đại là (−1; 4), điểm cực tiểu là (1; 0).

    Đồ thị hàm số có tâm đối xứng là (0; 2).

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Thực hành 1 trang 89 Toán 12 Tập 1: Vẽ đồ thị các hàm số bậc ba sau: a) y = x3; b) y = x3 – 3x; c) y = −x3 + 3x; d) y = x3 – 3x + 2.

    Thực hành 2 trang 89 Toán 12 Tập 1: Vẽ đồ thị các hàm số sau: a) y = x+1x−1 ; b) y = −x−1x−1 .

    Thực hành 3 trang 90 Toán 12 Tập 1: Vẽ đồ thị các hàm số sau: a) y = x2+x−1x−1; b) y = −x2+x−1x−1 ; c) y = x2+3x+1x+1 .

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài tập cuối chương 2 trang 65

    Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm

    Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

    Bài tập cuối chương 3 trang 84

    Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 118 17/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: