Nội dung bài viết

    Xem thêm

    Lý thuyết Hình chữ nhật – Toán lớp 8 Cánh diều

    Với lý thuyết Toán lớp 8 Bài 5: Hình chữ nhật chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 8.

    1 1,546 07/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 8 Bài 5: Hình chữ nhật - Cánh diều

    A. Lý thuyết Hình chữ nhật

    1. Khái niệm

    Lý thuyết Hình chữ nhật – Toán lớp 8 Kết nối tri thức (ảnh 1)

    Hình chữ nhật là tứ giác có bốn góc vuông.

    Chú ý: Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông và tứ giác đó là hình chữ nhật.

    2. Tính chất

    Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

    Nhận xét: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

    3. Dấu hiệu nhận biết

    - Hình bình hành có một góc vuông là hình chữ nhật

    - Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật

    Ví dụ:

    (ảnh 2)

    Hình b là hình chữ nhật vì có 4 góc vuông.

    B. Bài tập Hình chữ nhật

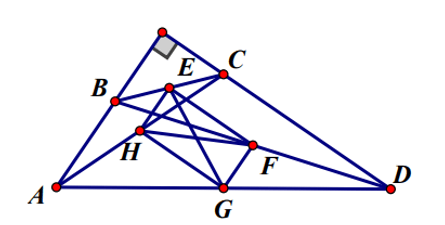
    Bài 1. Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.

    Hướng dẫn giải

    Lý thuyết Toán 8 Cánh diều Bài 5: Hình chữ nhật

    Vì E là trung điểm của BC; H là trung điểm của AC .

    Nên EH là đường trung bình của ΔBCD

    Suy ra EF // CI

    Kết hợp với AB ⊥ CD (gt) (4)

    Kết hợp (*), (3) và (4)

    Suy ra HE⊥ EF

    Suy ra HEF = 90° (***)

    Từ (**) và (***) ta có EFGH là hình chữ nhật.

    Từ đó hai đường chéo EG = FH.

    Vậy EG = FH.

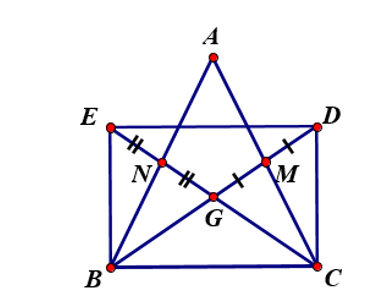
    Bài 2. Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?

    Hướng dẫn giải

    Lý thuyết Toán 8 Cánh diều Bài 5: Hình chữ nhật

    Ta có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm tam giác ABC.

    Theo tính chất trọng tâm tam giác ta có: BG = 2GM

    CG = 2GN

    Lại có: G đối xứng với với D qua M suy ra GM = MD hay GD = 2GM

    G đối xứng với E qua N suy ra GN = EN hay GE = 2GN

    Do đó BG = GD và CG = GE

    Suy ra G là trung điểm của BD và CE.

    Xét tứ giác BCDE có: G là trung điểm của đường chéo BD

    G là trung điểm đường chéo CE

    Suy ra tứ giác BCDE là hình bình hành.

    Lại có: ∆ABC cân tại A nên AB = AC.

    Mà M là trung điểm của AC, N là trung điểm AB nên BN = CM.

    Xét ∆BNC và ∆CMB có:

    Cạnh BC chung

    BN = CM

    NBC^=MCB^(do tam giác ABC cân tại A)

    Do đó ∆BNC = ∆CMB (c.g.c)

    Suy ra CN = BM (hai cạnh tương ứng)

    Mà CN=34EC và BM=34BD

    Do đó EC = BD.

    Xét hình bình hành BCDE có hai đường chéo EC và BD bằng nhau.

    Vậy tứ giác BCDE là hình chữ nhật.

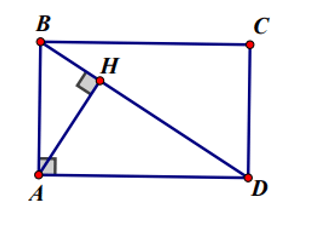
    Bài 3. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HB = 2 cm, HD = 6 cm. Tính độ dài AB, AD.

    Hướng dẫn giải

    Lý thuyết Toán 8 Cánh diều Bài 5: Hình chữ nhật

    Ta có: BD = HB + HD = 2 + 6 = 8 (cm).

    Xét tam giác giác BHA vuông tại H ta có: BH2 + AH2 = AB2

    Suy ra AH2 = AB2 – BH2

    Suy ra AH2 = AB2 – 4 (1)

    Xét tam giác AHD vuông tại H ta có: HD2 + AH2 = AD2

    Suy ra AH2 = AD2 – HD2

    Suy ra AH2 = AD2 – 3 (2)

    Từ (1) và (2) suy ra AB2 – 4 = AD2 – 36 (3)

    Xét tam giác ABD vuông tại A có:

    AB2 + AD2 = DB2 = 82 = 64

    Thay AB2 = 64 – AD2 vào (3). Giải ra ta được AD2 = 48 hay AD=43 .

    Suy ra AB = 4 cm.

    Vậy AD=43 cm và AB = 4 cm.

    Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Cánh diều hay, chi tiết khác:

    Lý thuyết Bài 6: Hình thoi

    Lý thuyết Bài 7: Hình vuông

    Lý thuyết Bài 1: Thu thập và phân loại dữ liệu

    Lý thuyết Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ

    Lý thuyết Bài 3: Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,546 07/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: