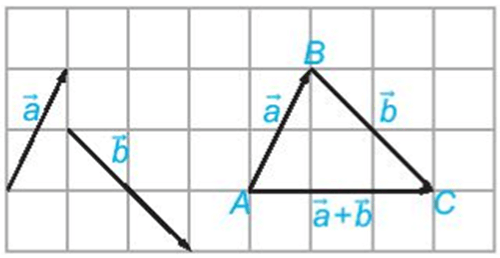
Trắc nghiệm Ôn tập chương 1 Hình học 10 (có đáp án)
Trắc nghiệm Toán 10 Hình học Ôn tập chương 1
-
843 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Tứ giác ABCD có →AB=→DC⇒ABCD là hình bình hành (1) , nên →AD=→BC.
Mà|→AB|=|→BC|(2).
Từ (1) và (2) ta có ABCD là hình thoi nên |→CD|=|→BC|.
Câu 2:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có →BA=(−4;3),→BC=(8;−7)⇒→BA, →BC không cùng phương nên A, B, C không thẳng hàng,→CE=(m−10;6) . Để ABCE là hình thang có một đáy là CE thì →CE cùng chiều với →BA⇒m−10−4=63>0⇔m=2 .
Vậy E(2;1).
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
2MA2+MB2+2MC2+MD2=9a2
⇔2(→MO+→OA)2+(→MO+→OB)2+2(→MO+→OC)2+(→MO+→OD)2=9a2
⇔6MO2+2OA2+OB2+2OC2+OD2+2→MO(2→OA+2→OC+→OB+→OD)⏟→0=9a2
⇔6MO+23a2=9a2⇔MO=a
Vậy tập hợp các điểm M là đường tròn tâm O bán kính R=a.
Câu 4:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
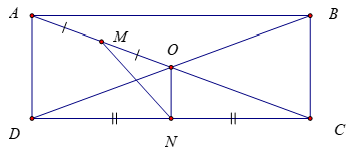
→MN=→MO+→ON=14→AC+12→AD
=14(→AB+→BC)+12→AD
=14(→AB+→AD)+12→AD
=14→AB+34→AD
⇒a=14;b=34 .
Vậy a+b=1.
Câu 6:
15/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
→AB=(4; 3)⇒→u=2→AB=(8; 6).
Câu 7:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Điểm I là trọng tâm tam giác ABC
⇔{xI=xA+xB+xC3yI=yA+yB+yC3
⇔{xC=3xI−xA−xByC=3yI−yA−yB
⇔{xC=3−3−(−1)=1yC=−3−(−1)−2=−4
Vậy điểm C(1; −4).
Câu 8:
23/07/2024Xét các mệnh đề sau
(I): Véc tơ – không là véc tơ có độ dài bằng 0.
(II): Véc tơ – không là véc tơ có nhiều phương.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Véc tơ – không là véc tơ có điểm đầu, điểm cuối trùng nhau nên có độ dài bằng 0.
Véc tơ – không cùng phương với mọi véc tơ.
Câu 9:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Theo quy tắc đường chéo hình bình hành, ta có:
|→AD+→AB|=|→AC|=AC
=AB√2=a√2.
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Tọa độ trung điểm I của đoạn thẳng: AB
{xI=xA+xB2yI=yA+yB2
⇒{xI=3yI=−2⇒I(3;−2).
Câu 11:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Do G là trọng tâm tam giác ABC nên
{xG=xA+xB+xC3yG=yA+yB+yC3
⇔{xC=3xG−xA−xByC=3yG−yA−yB⇔{xC=4yC=−5
Vậy C(4; −5).
Câu 12:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Theo định nghĩa phép nhân véc tơ với một số.
Câu 13:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có:
→AB=(2; −3)⇒2→AB=(4; −6)
→BC=(−3; 2)
Nên →u=2→AB+→BC=(1; −4).
Câu 14:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
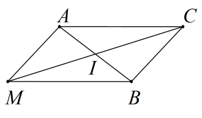
Với mọi điểm M, ta dựng hình bình hành AMBC.
Khi đó, theo quy tắc hình bình hành:
→MA+→MB=→MC=2→MI .
Câu 15:
10/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : C
Lời giải
Gọi M là trung điểm BC, ta có:
→AG=23→AM
=23.12(→AB+→AC)
=13(→AB+→AC).
*Phương pháp giải:
Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:
→MA+→MB=2→MI ( M tùy ý )
*Lý thuyết:
- Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:
→MA+→MB=2→MI ( M tùy ý )
→IA+→IB=→0
- Quy tắc trọng tâm: Với G là trọng tâm tam giác ABC thì ta có:
→MA+→MB+→MC=3→MG ( M tùy ý )
→GA+→GB+→GC=→0
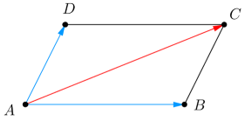
- Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì →AB+→AD=→AC.
B. Các công thức.
- Quy tắc trung điểm: I là trung điểm của AB
→IA+→IB=→0
→MA+→MB=2→MI ( M tùy ý )
- Quy tắc trọng tâm: G là trọng tâm tam giác ABC
→MA+→MB+→MC=3→MG ( M tùy ý )
→GA+→GB+→GC=→0
- Quy tắc hình hình hành: →AB+→AD=→AC ( ABCD là hình bình hành )
Xem thêm
Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vecto (2024) chi tiết nhấtCâu 16:
08/09/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
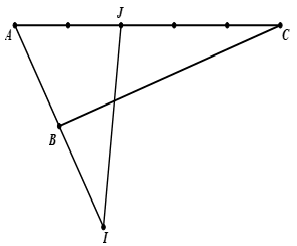
Ta có:
→IJ=→IA+→AJ
=−2→AB+25→AC
=25→AC−2→AB
* Giải thích
Sử dụng các vector để biểu diễn các cạnh của tam giác và các điểm I, J.
Áp dụng các phép toán vector để tìm các đại lượng cần thiết.
Xem thêm các bài toán hay, chi tiết khác
Lý thuyết Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức
Câu 17:
23/07/2024Trong mặt phẳng Oxy, cho hình bình hành ABCD có A(2;−3), B(4;5) và G(0;−133) là trọng tâm tam giác ADC. Tọa độ đỉnh D là
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Cách 1: Gọi D(a; b). Vì G(0;−133) là trọng tâm tam giác ADC nên
→BD=32→BG
⇔{a−4=32(0−4)b−5=32(−133−5)⇔{a=−2b=−9
⇒D(−2; −9)
Cách 2: Gọi I là trọng tâm tam giác ABC suy ra I là trung điểm BG ⇒I(2; 13).
Lại có G(0;−133) là trung điểm DI nên suy ra D(−2; −9).
Câu 18:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Hai vectơ đối nhau là hai vectơ có cùng độ dài và ngược hướng.
Câu 19:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
![]()
Ta thấy →MN và →MP cùng hướng.
Câu 20:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
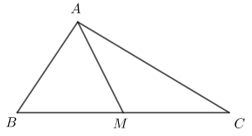
Ta có →AB+→AC=2→AM
⇒M là trung điểm của BC
Câu 21:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có:
→MN+→PQ+→RN+→NP+→QR=→MN+(→PQ+→QR+→RN+→NP)=→MN+→0=→MN.
Câu 22:
23/09/2024 Xem đáp án
Xem đáp án
Đáp án: B
*Lời giải
→OA=→OB−→BA⇔→OA−→OB
=−→BA⇔→BA=−→BA nên A sai
→OA=→CA−→CO⇔→OA−→CA
=−→CO⇔→OA+→AC=−→CO⇔→OC=−→CO
nên B đúng.
*Lý thuyết liên quan
1. Tổng của hai vectơ
– Cho hai vectơ →a và →b. Lấy một điểm A tùy ý và vẽ →AB=→a, →BC=→b. Khi đó vectơ →ACđược gọi là tổng của hai vectơ →a và →b và được kí hiệu là →a + →b.
– Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.
– Quy tắc ba điểm: Với ba điểm bất kì A, B, C, ta có →AB+→BC=→AC .
– Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì →AB+→BC=→AC.
– Với ba vectơ; →a, →b, →c tùy ý :
+ Tính chất giao hoán: →a+ →b= →b + →a;
+ Tính chất kết hợp: (→a + →b) + →c = →a + (→b + →c);
+ Tính chất của vectơ–không: →a + →0 = →0+ →a = →a.
Chú ý: Do các vectơ (→a + →b) + →c và →a + (→b + →c) bằng nhau, nên ta còn viết chúng dưới dạng →a + →b + →c và gọi là tổng của ba vectơ →a, →b, →c. Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng dấu ngoặc.
2. Hiệu của hai vectơ
– Vectơ có cùng độ dài và ngược hướng với vectơ →a được gọi là vectơ đối của vectơ →a. Vectơ đối của vectơ →a kí hiệu là –→a.
– Vectơ được coi là vectơ đối của chính nó.
– Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng →0.
– Vectơ →a+ (–→b) được gọi là hiệu của hai vectơ →a và →b và được kí hiệu là →a– →b. Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.
– Nếu →b+ →c= →a thì →a– →b = →a+ (–→b) = →c + →b+ (–→b) = →c+ →0 = →c.
– Quy tắc hiệu: Với ba điểm O, M, N, ta có →MN=→MO+→ON=(−→OM)+→ON=→ON−→OM.
Nhận xét: Trong vật lý, trọng tâm của một vật là điểm đặt của trọng lực tác dụng lên vật đó. Đối với một vật mỏng hình đa giác A1A2…An thì trọng tâm của nó là điểm G thỏa mãn →GA1+→GA2+...+→GAn=→0.
Xem thêm các bài toán hay, chi tiết khác
Lý thuyết Toán 10 Bài 8: Tổng và hiệu của hai vectơ - Kết nối tri thức
Câu 23:
10/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Tọa độ trung điểm của đoạn thẳng AB là I(1+02; 0−22) hay I(12;−1).
Câu 24:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Gọi M(x; y)
⇒{→MB=(2−x; 3−y)→MC=(−1−x; −2−y)
⇒2→MB+3→MC=(−5x+1;−5y)
Khi đó 2→MB+3→MC=→0.
⇔{−5x+1=0−5y=0⇔{x=15y=0
Vậy M(15; 0).
Câu 25:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có:
→u=m→a+n→b
⇔{−m+n=2−2m−3n=−4
⇔{m=−25n=85.
Suy ra m−n=−2
Câu 26:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
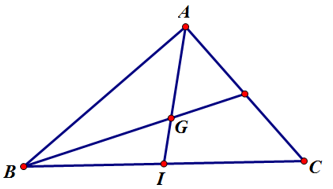
|→IB+→IC+→IA|=|→0+→IA|=|→IA|=IA (Do I là trung điểm BC) nên khẳng định ở A đúng.
|→AB+→AC|=|2→AI|=2AI (Do I là trung điểm BC) nên khẳng định ở C đúng.
|→AB+→AC|=2AI=3GA (Do G là trọng tâm tam giác ABC) nên khẳng định ở D đúng.
|→IB+→IC|=|→0|=0 (Do I là trung điểm BC) nên khẳng định ở B sai.
Câu 27:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
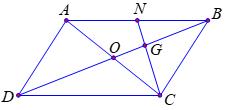
Vì G là trọng tâm ΔABC nên
→GA+→GB+→GC=→0⇔→GA=−(→GB+→GC)
Suy ra →GA=−(−13→BD+23→NC)
=13→BD−23→NC.
Câu 28:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có →v =3→i −m→j
⇒→v =(3 ; −m).
Hai vectơ →u ,→v cùng phương
⇔3−2=−m1⇔m=32.
Câu 29:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có:
m→a+n→b=→c ⇔ {2m−3n=−4m+4n=9 ⇔ {m=1n=2 .
Câu 30:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
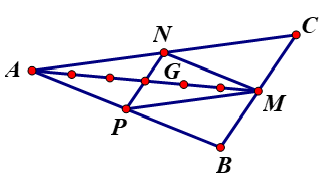
Vì G là trọng tâm tam giác ABC nên G cũng là trọng tâm tam giác MNP.
Tọa độ điểm G là
{xG=xM+xN+xP3yG=yM+yN+yP3
⇔{xG=−43yG=−43
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập chương 1 Hình học 10 (có đáp án) (842 lượt thi)
- 80 câu trắc nghiệm Vectơ cơ bản (2303 lượt thi)
- 75 câu trắc nghiệm Vectơ nâng cao (2062 lượt thi)
- Trắc nghiệm Ôn tập chương 1: Vecto có đáp án (321 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 1 Hình học có đáp án (Nhận biết) (353 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 1 Hình học có đáp án (Thông hiểu) (349 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 1 Hình học có đáp án (Vận dụng) (286 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 1 Hình học có đáp án (346 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Các định nghĩa (có đáp án) (881 lượt thi)
- Trắc nghiệm Hệ trục tọa độ (có đáp án) (869 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ (có đáp án) (859 lượt thi)
- Trắc nghiệm Tích của vectơ với một số có đáp án (Nhận biết) (838 lượt thi)
- Trắc nghiệm Tích của vectơ với một số (có đáp án) (764 lượt thi)
- Trắc nghiệm Tích của vecto với một số có đáp án (589 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Thông hiểu) (583 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Vận dụng) (576 lượt thi)
- Trắc nghiệm Tích của vectơ với một số có đáp án (Vận dụng) (483 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Tổng hợp) (475 lượt thi)