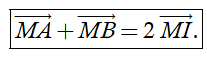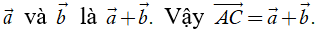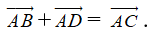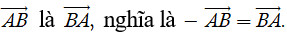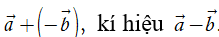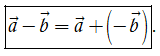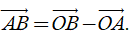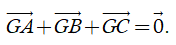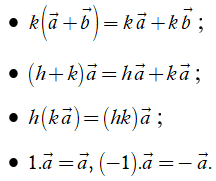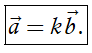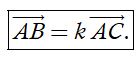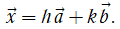32 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập chương 1: Vecto có đáp án

Cho đa giác lồi n cạnh. Có bao nhiêu vectơ khác $\vec{0}$ mà giá của chúng tương ứng chứa các đường chéo của đa giác đã cho?

A. $\frac{n (n - 1)}{2}$

B. $\frac{n (n - 3)}{2}$

C. $2 n$

D. n(n-3)

Xem đáp án

Tổng số cạnh và đường chéo của đa giác n cạnh là n(n-1)/2, suy ra số đường chéo của đa giác là

Vì mỗi đường chéo xác định hai vectơ, nên tổng số vectơ là n(n – 3)

Đáp án D

Câu 6:

Cho hai vectơ $\vec{a}, \vec{b}$ khác vectơ $\vec{0}$ , không cùng phương và có độ dài bằng nhau. Khi đó giá của hai vectơ $\vec{a} + \vec{b}$ và $\vec{a} - \vec{b}$ thỏa mãn điều kiện nào sau đây?

A. Cắt và không vuông góc

B. Vuông góc với nhau

C. Song song với nhau

D. Trùng nhau

Xem đáp án

Đáp án B

Câu 7:

17/07/2024

Cho tam giác cân ABC (AB = AC). Tam giác ABC là tam giác đều nếu:

A. $|\vec{A B}| = |\vec{A B} - \vec{A C}|$

B. $|\vec{A B}| = |\vec{A B} + \vec{A C}|$

C. $|\vec{A C}| = |\vec{A B} + \vec{A C}|$

D. $|\vec{B C}| = |\vec{A C} - \vec{A B}|$

Xem đáp án

Đáp án A

Câu 8:

10/07/2024

Cho tam giác ABC vuông cân tại C và $A B = \sqrt{2} .$ Tính độ dài của $\vec{A B} + \vec{A C} .$

A. $|\vec{A B} + \vec{A C}| = \sqrt{5} .$

B. $|\vec{A B} + \vec{A C}| = 2 \sqrt{5} .$

C. $|\vec{A B} + \vec{A C}| = \sqrt{3} .$

D. $|\vec{A B} + \vec{A C}| = 2 \sqrt{3} .$

Xem đáp án

Câu 9:

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm đối xứng với M qua N. Khi đó khẳng định nào sau đây đúng?

A. $\vec{M K} = \vec{A D} - \vec{B C}$

B. $\vec{M K} = \vec{A D} + \vec{B C}$

C. $\vec{M K} = \vec{A B} - \vec{C D}$

D. $\vec{M K} = \vec{A C} - \vec{B D}$

Xem đáp án

Tứ giác DMCK có hai đường chéo cắt nhau tại trung điểm mỗi đường (N là trung điểm của MK và CD). Do đó, tứ giác DMCK là hình bình hành.

Theo quy tắc hình bình hành ta có:

Đáp án B

Câu 10:

Cho tam giác ABC. Điểm M thỏa mãn điều kiện $\vec{M A} - \vec{M B} + \vec{M C} = \vec{0}$ thì điều kiện cần và đủ là

A. M là điểm sao cho tứ giác ABMC là hình bình hành

B. M là trọng tâm tam giác ABC

C. M là điểm sao cho tứ giác BAMC là hình bình hành

D. M thuộc trung trực của AB

Xem đáp án

Đáp án C

Câu 11:

Cho tam giác ABC đều cạnh a ; H là trung điểm của BC. Tính $|\vec{C A} - \vec{H C}| .$

A. $|\vec{C A} - \vec{H C}| = \frac{a}{2} .$

B. $|\vec{C A} - \vec{H C}| = \frac{3 a}{2} .$

C. $|\vec{C A} - \vec{H C}| = \frac{2 \sqrt{3} a}{3} .$

D. $|\vec{C A} - \vec{H C}| = \frac{a \sqrt{7}}{2} .$

Xem đáp án

Gọi D là điểm thỏa mãn tứ giác ACHD là hình bình hành

$\Rightarrow A H B D$ là hình chữ nhật.

$|\vec{C A} - \vec{H C}| = |\vec{C A} + \vec{C H}| = |\vec{C D}| = C D .$

$C D = \sqrt{B D^{2} + B C^{2}} = \sqrt{A H^{2} + B C^{2}} = \sqrt{\frac{3 a^{2}}{4} + a^{2}} = \frac{a \sqrt{7}}{2} .$

Đáp án D

Câu 12:

23/07/2024

Cho hình bình hành ABCD. Tập hợp tất cả các điểm M thỏa mãn đẳng thức $\vec{M A} + \vec{M B} - \vec{M C} = \vec{M D}$ là

A. một đường tròn.

B. một đường thẳng.

C. tập rỗng.

D. một đoạn thẳng.

Xem đáp án

Câu 13:

Cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ bất kì. Khẳng định nào sau đây sai?

A. $|\vec{a} + \vec{b} + \vec{c}| = |\vec{a}| + |\vec{b}| + |\vec{c}|$

B. $|\vec{a} + \vec{b} + \vec{c}| \leq |\vec{a}| + |\vec{b}| + |\vec{c}|$

C. $|\vec{a} + \vec{b} + \vec{c}| \leq |\vec{a} + \vec{b}| + |\vec{c}|$

D. $|\vec{a} + \vec{b} + \vec{c}| \leq |\vec{a}| + |\vec{b} + \vec{c}|$

Xem đáp án

Đáp án A

Câu 14:

Cho tam giác OAB vuông cân tại O, cạnh OA= a. Tính $|2 \vec{O A} - \vec{O B}| .$

A. a

B. $(1 + \sqrt{2}) a .$

C. $a \sqrt{5} .$

D. $2 a \sqrt{2} .$

Xem đáp án

Câu 15:

16/07/2024

Cho tam giác ABC có M là trung điểm của BC; I là trung điểm của AM. Khẳng định nào sau đây đúng ?

A. $\vec{I B} + 2 \vec{I C} + \vec{I A} = \vec{0} .$

B. $\vec{I B} + \vec{I C} + 2 \vec{I A} = \vec{0} .$

C. $2 \vec{I B} + \vec{I C} + \vec{I A} = \vec{0} .$

D. $\vec{I B} + \vec{I C} + \vec{I A} = \vec{0} .$

Xem đáp án

Câu 16:

17/07/2024

Cho tam giác ABC có M là trung điểm của BC; I là trung điểm của AM. Khẳng định nào sau đây đúng ?

A. $\vec{A I} = \frac{1}{4} (\vec{A B} + \vec{A C}) .$

B. $\vec{A I} = \frac{1}{4} (\vec{A B} - \vec{A C}) .$

C. $\vec{A I} = \frac{1}{4} \vec{A B} + \frac{1}{2} \vec{A C} .$

D. $\vec{A I} = \frac{1}{4} \vec{A B} - \frac{1}{2} \vec{A C} .$

Xem đáp án

Câu 17:

14/07/2024

Cho hình thang ABCD có đáy là AB và CD. Gọi M và N lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai?

A. $\vec{M N} = \vec{M D} + \vec{C N} + \vec{D C} .$

B. $\vec{M N} = \vec{A B} - \vec{M D} + \vec{B N} .$

C. $\vec{M N} = \frac{1}{2} (\vec{A B} + \vec{D C}) .$

D. $\vec{M N} = \frac{1}{2} (\vec{A D} + \vec{B C}) .$

Xem đáp án

Vì M; N lần lượt là trung điểm của AD; BC

$\{\begin{cases} \vec{M A} + \vec{M D} = \vec{0} \\ \vec{B N} + \vec{C N} = \vec{0} \end{cases} .$

Dựa vào đáp án, ta có nhận xét sau:

A đúng, vì :

$\vec{M D} + \vec{C N} + \vec{D C} = \vec{M N} = (\vec{M D} + \vec{D C}) + \vec{C N} = \vec{M C} + \vec{C N} = \vec{M N} .$

B đúng, vì $\vec{A B} - \vec{M D} + \vec{B N} = (\vec{A B} + \vec{B N}) - \vec{M D} = \vec{A N} - \vec{A M} = \vec{M N} .$

C đúng, vì $\vec{M N} = \vec{M A} + \vec{A B} + \vec{B N}$ và $\vec{M N} = \vec{M D} + \vec{D C} + \vec{C N} .$

Suy ra

$2 \vec{M N} = (\vec{M A} + \vec{M D}) + \vec{A B} + \vec{D C} + (\vec{B N} + \vec{C N}) = \vec{0} + \vec{A B} + \vec{D C} + \vec{0} = \vec{A B} + \vec{D C}$

$\Rightarrow \vec{M N} = \frac{1}{2} (\vec{A D} + \vec{B C}) .$

D sai, vì theo phân tích ở đáp án C.

Chọn D.

Câu 18:

05/07/2024

Cho hình bình hành ABCD có M là trung điểm của AB. Khẳng định nào sau đây đúng?

A. $\vec{D M} = \frac{1}{2} \vec{C D} + \vec{B C} .$

B. $\vec{D M} = \frac{1}{2} \vec{C D} - \vec{B C} .$

C. $\vec{D M} = \frac{1}{2} \vec{D C} - \vec{B C} .$

D. $\vec{D M} = \frac{1}{2} \vec{D C} + \vec{B C} .$

Xem đáp án

Câu 19:

Cho tam giác đều ABC và điểm I thỏa mãn $\vec{I A} = 2 \vec{I B} .$ Mệnh đề nào sau đây đúng?

A. $\vec{C I} = \frac{\vec{C A} - 2 \vec{C B}}{3} .$

B. $\vec{C I} = \frac{\vec{C A} + 2 \vec{C B}}{3} .$

C. $\vec{C I} = - \vec{C A} + 2 \vec{C B} .$

D. $\vec{C I} = \frac{\vec{C A} + 2 \vec{C B}}{- 3} .$

Xem đáp án

Đáp án C

Câu 20:

Cho tam giác ABC và một điểm M tùy ý. Mệnh đề nào sau đây đúng?

A. $2 \vec{M A} + \vec{M B} - 3 \vec{M C} = \vec{A C} + 2 \vec{B C} .$

B. $2 \vec{M A} + \vec{M B} - 3 \vec{M C} = 2 \vec{A C} + \vec{B C} .$

C. $2 \vec{M A} + \vec{M B} - 3 \vec{M C} = 2 \vec{C A} + \vec{C B} .$

D. $2 \vec{M A} + \vec{M B} - 3 \vec{M C} = 2 \vec{C B} - \vec{C A} .$

Xem đáp án

$\begin{array}{l} 2 \vec{M A} + \vec{M B} - 3 \vec{M C} = 2 (\vec{M C} + \vec{C A}) + (\vec{M C} + \vec{C B}) - 3 \vec{M C} \\ = 2 \vec{M C} + 2 \vec{C A} + \vec{M C} + \vec{C B} - 3 \vec{M C} = 2 \vec{C A} + \vec{C B} . \end{array}$

Đáp án C

Câu 21:

21/07/2024

Cho tam giác ABC và điểm M thỏa mãn $2 \vec{M A} + \vec{M B} = \vec{C A} .$ Khẳng định nào sau đây là đúng?

A. M trùng A

B. M trùng B.

C. M trùng C

D. M là trọng tâm của tam giác ABC.

Xem đáp án

$2 \vec{M A} + \vec{M B} = \vec{C A} \Leftrightarrow 2 \vec{M A} + \vec{M B} = \vec{C M} + \vec{M A} .$

$\Leftrightarrow \vec{M A} + \vec{M B} = - \vec{M C} \Leftrightarrow \vec{M A} + \vec{M B} + \vec{M C} = \vec{0} .$ (*)

Đẳng thức (*) suy ra M là trọng tâm của tam giác ABC.

Chọn D.

Câu 22:

13/07/2024

Cho hình chữ nhật ABCD và số thực k> 0. Tập hợp các điểm M thỏa mãn đẳng thức $|\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D}| = k$

A. một đoạn thẳng.

B. một đường thẳng

C. một đường tròn.

D. một điểm

Xem đáp án

Gọi I là tâm của hình chữ nhật ABCD ta có $\{\begin{cases} 2 \vec{M I} = \vec{M A} + \vec{M C} \\ 2 \vec{M I} = \vec{M B} + \vec{M D} \end{cases}, \forall M .$

Do đó :

$\begin{array}{l} |\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D}| = k \\ \Leftrightarrow |(\vec{M A} + \vec{M C}) + (\vec{M B} + \vec{M D})| = k \\ \Leftrightarrow |2 \vec{M I} + 2 \vec{M I}| = k \Leftrightarrow 4 |\vec{M I}| = k \Leftrightarrow |\vec{M I}| = \frac{k}{4} . \end{array} (*)$

Vì I là điểm cố định nên tập hợp các điểm M thỏa mãn đẳng thức (*) là đường tròn tâm I bán kính $R = \frac{k}{4} .$

Chọn C.

Câu 23:

21/07/2024

Cho hai điểm A, B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức $|2 \vec{M A} + \vec{M B}| = |\vec{M A} + 2 \vec{M B}|$ là

A. đường trung trực của đoạn thẳng AB

B. đường tròn đường kính AB

C. đường trung trực đoạn thẳng IA

D. đường tròn tâm A; bán kính AB.

Xem đáp án

Chọn điểm E thuộc đoạn AB sao cho EB = 2EA $\Rightarrow 2 \vec{E A} + \vec{E B} = \vec{0} .$

Chọn điểm F thuộc đoạn AB sao cho FA = 2FB $\Rightarrow 2 \vec{F B} + \vec{F A} = \vec{0} .$

Ta có

$\begin{array}{l} |2 \vec{M A} + \vec{M B}| = |\vec{M A} + 2 \vec{M B}| \\ \Leftrightarrow |2 \vec{M E} + 2 \vec{E A} + \vec{M E} + \vec{E B}| = |\vec{M F} + \vec{F A} + 2 \vec{M F} + 2 \vec{F B} | \end{array}$

$\begin{array}{l} \Leftrightarrow |3 \vec{M E} + \underset{\vec{0}}{\underset{⏟}{2 \vec{E A} + \vec{E B}}}| = |3 \vec{M F} + \underset{\vec{0}}{\underset{⏟}{\vec{F A} + 2 \vec{F B}}}| \\ \Leftrightarrow |3 \vec{M E}| = |3 \vec{M F}| \Leftrightarrow M E = M F . \end{array} (*)$

Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.

Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF

Vậy tập hợp các điểm M thỏa mãn $|2 \vec{M A} + \vec{M B}| = |\vec{M A} + 2 \vec{M B}|$ là đường trung trực của đoạn thẳng AB.

Chọn A.

Câu 24:

23/07/2024

Cho tứ giác ABCD. M và N lần lượt là trung điểm của AB, CD. Đẳng thức nào sau đây là đúng?

A. $M N = \frac{B C + A D}{2}$

B. $\vec{M N} = \vec{B C} + \vec{A D}$

C. $\vec{M N} = \vec{A C} + \vec{B D}$

D. $\vec{M N} = \frac{1}{2} (\vec{B C} + \vec{A D})$

Xem đáp án

Đáp án D

Câu 25:

Tóm tắt lý thuyết Toán lớp 10 Chương 5: Vectơ - Chân trời sáng tạo

Cho hình thang ABCD, hai đường chéo AC và BD cắt nhau tại O. Qua O kẻ MN song song với AB (AB là đáy của hình thang, M∈AD ,N∈BC). Đặt $|\vec{A B}| = a; |\vec{D C}| = b$ . Khi đó khẳng định nào sau đây là đúng?

A. $\vec{M N} = \frac{a \vec{A B} + b \vec{D C}}{a + b}$

B. $\vec{M N} = \frac{b \vec{A B} + a \vec{D C}}{a + b}$

C. $\vec{M N} = \frac{a \vec{A B} - b \vec{D C}}{a + b}$

D. $\vec{M N} = \frac{b \vec{A B} - a \vec{D C}}{a + b}$

Xem đáp án

Đáp án B

Câu 26:

08/11/2024

Cho hình vuông ABCD cạnh a, tâm O. Tính $|\vec{O B} + \vec{O C}|$

A. $|\vec{O B} + \vec{O C}| = a .$

B. $|\vec{O B} + \vec{O C}| = a \sqrt{2} .$

C. $|\vec{O B} + \vec{O C}| = \frac{a}{2} .$

D. $|\vec{O B} + \vec{O C}| = \frac{a \sqrt{2}}{2} .$

Xem đáp án

Đáp án đúng: A

*Lời giải:

Gọi M là trung điểm của BC.

Tam giác ABC có O ; M lần lượt là trung điểm của AC ; BC nên OM là đường trung bình của

tam giác

Suy ra : AB = 2OM.

Ta có $|\vec{O B} + \vec{O C}| = 2 |\vec{O M}| = 2 O M = A B = a .$

*Phương pháp giải:

- Áp dụng: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M thì ta có

*Lý thuyết nắm thêm và các dạng toán về các phép toán vectơ :

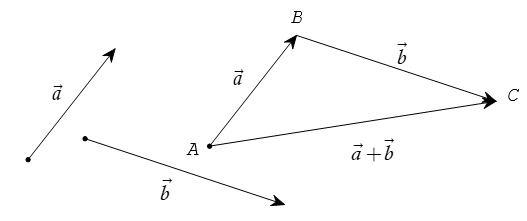
1. Tổng của hai vectơ

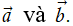
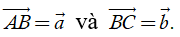
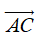
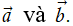
Định nghĩa. Cho hai vectơ Lấy một điểm A tùy ý, vẽ Vectơ được gọi là tổng của hai vectơ Ta kí hiệu tổng của hai vectơ

Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.

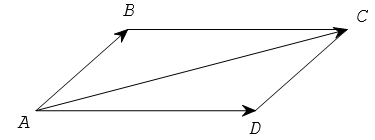
2. Quy tắc hình bình hành

Nếu ABCD là hình bình hành thì

3. Tính chất của phép cộng các vectơ

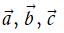
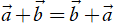
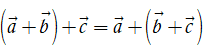
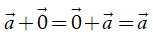
Với ba vectơ tùy ý ta có

• (tính chất giao hoán);

• (tính chất kết hợp);

• (tính chất của vectơ – không).

4. Hiệu của hai vectơ

a) Vectơ đối

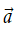
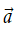
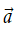
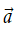
Cho vectơ Vectơ có cùng độ dài và ngược hướng với được gọi là vectơ đối của vectơ , kí hiệu là -.

Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của

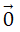
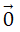
Đặc biệt, vectơ đối của vectơ là vectơ .

b) Định nghĩa hiệu của hai vectơ

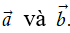
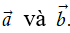
Định nghĩa. Cho hai vectơ Ta gọi hiệu của hai vectơ là vectơ

Như vậy

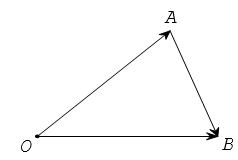
Từ định nghĩa hiệu của hai vectơ, suy ra với ba điểm O, A, B tùy ý ta có

Chú ý

1) Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ.

2) Với ba điểm tùy ý A, B, C ta luôn có

(quy tắc ba điểm);

(quy tắc trừ).

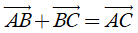
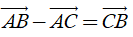
5. Áp dụng

a) Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi

b) Điểm G là trọng tâm của tam giác ABC khi và chỉ khi

TÍCH CỦA VECTƠ VỚI MỘT SỐ

1. Định nghĩa

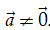
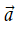
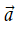
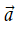
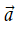
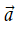
Cho số k ≠ 0 và vectơ Tích của vectơ với số k là một vectơ, kí hiệu là k , cùng hướng với nếu k > 0, ngược hướng với nếu k < 0 và có độ dài bằng |k|.||

2. Tính chất

Với hai vectơ 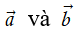bất kì, với mọi số h và k, ta có

3. Trung điểm của đoạn thẳng và trọng tâm của tam giác

a) Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M thì ta có

b) Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M thì ta có

$\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G} .$

4. Điều kiện để hai vectơ cùng phương

Điều kiện cần và đủ để hai vectơ 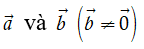cùng phương là có một số k để

Nhận xét. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để

5. Phân tích một vectơ theo hai vectơ không cùng phương

Cho hai vectơ 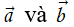không cùng phương. Khi đó mọi vectơ đều phân tích được một cách duy nhất theo hai vectơ nghĩa là có duy nhất cặp số h, k sao cho

Xem thêm các bài viết liên quan hay, chi tiết:

Giải Toán 10 (Chân trời sáng tạo): Bài tập cuối chương 5

TOP 30 câu Trắc nghiệm Ôn tập chương 5 (Chân trời sáng tạo 2024) có đáp án - Toán 10

Câu 27:

Cho tam giác ABC với AB = c, BC = a, CA = b. Gọi CM là đường phân giác trong của góc C (M∈AB). Biểu thị nào sau đây là đúng?

A. $\vec{M A} = \frac{b}{a} \vec{M B}$

B. $\vec{M A} = \frac{c}{a} \vec{M B}$

C. $\vec{M A} = - \frac{b}{a} \vec{M B}$

D. $\vec{M A} = - \frac{c}{a} \vec{M B}$

Xem đáp án

Áp dụng tính chất của đường phân giác ta có

Đáp án C

Câu 28:

Cho ba vectơ $\vec{a} = (2; 1), \vec{b} = (3; 4), \vec{c} = (7; 2) .$ Giá trị của k; h để $\vec{c} = k . \vec{a} + h . \vec{b}$ là

A. $k = 2,5; h = - 1,3.$

B. $k = 4,6; h = - 5,1.$

C. $k = 4,4; h = - 0,6.$

D. $k = 3,4; h = - 0,2.$

Xem đáp án

$\begin{array}{l} k . \vec{a} = (2 k; k) \\ h . \vec{b} = (3 h; 4 h) \end{array}\} \Rightarrow k . \vec{a} + h . \vec{b} = (2 k + 3 h; k + 4 h) .$

$\vec{c} = k . \vec{a} + h . \vec{b} \Leftrightarrow \{\begin{cases} 7 = 2 k + 3 h \\ 2 = k + 4 h \end{cases} \Leftrightarrow \{\begin{cases} k = 4,4 \\ h = - 0,6 \end{cases} .$

Đáp án C

Câu 29:

10/07/2024

Tam giác ABC có C(–2; –4), trọng tâm G(0; 4), trung điểm cạnh BC là M(2; 0). Tọa độ điẻm A và B là:

A. A(4; 12) , B(4; 6)

B. A(–4; –12), B(6; 4)

C. A(–4; 12), B(6; 4)

D. A(4; –12), B(–6; 4)

Xem đáp án

$\{\begin{matrix} x_{M} = \frac{x_{B} + x_{C}}{2} \\ y_{M} = \frac{y_{B} + y_{C}}{2} \end{matrix} \Leftrightarrow \{\begin{matrix} x_{B} = 2 x_{M} - x_{C} = 2.2 - (- 2) = 6 \\ y_{B} = 2 y_{M} - y_{C} = 2.0 - (- 4) = 4 \end{matrix} \Rightarrow B (6; 4)$

Do G là trọng tâm tam giác ABC nên:

$\{\begin{matrix} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} \end{matrix} \Leftrightarrow \{\begin{matrix} x_{A} = 3 x_{G} - x_{B} - x_{C} = 3.0 - 6 - (- 2) = - 4 \\ y_{A} = 3 y_{G} - y_{B} - y_{C} = 3.4 - 4 - (- 4) = 12 \end{matrix} \Rightarrow A (- 4; 12)$

Đáp án C

Câu 30:

Cho các vectơ $\vec{a} (1; 3); \vec{b} (2; 5); \vec{c} (7; 19)$ . Phân tích vectơ $\vec{c}$ theo các vectơ $\vec{a}; \vec{b}$ là:

A. $\vec{c} = 3 \vec{a} + 2 \vec{b}$

B. $\vec{c} = 3 \vec{a} - 2 \vec{b}$

C. $\vec{c} = 2 \vec{a} + 3 \vec{b}$

D. $\vec{c} = 2 \vec{a} - 3 \vec{b}$

Xem đáp án

Đáp án A

Câu 31:

Cho các vectơ $\vec{a} (- 1; 2), \vec{b} (3; 5)$ . Tìm các số thực x, y sao cho $x \vec{a} + y \vec{b} = \vec{0}$ .

A. x = 0; y = 1

B. x = 0; y = 0

C. x = 1; y = 0

D. x = 1; y = 1

Xem đáp án

Đáp án B

Câu 32: