Trắc nghiệm Tích của vectơ với một số (có đáp án)
Trắc nghiệm Toán 10 Bài 3: Tích của vectơ với một số
-
741 lượt thi
-
25 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có ba điểm phân biệt A,B,C thẳng hàng khi và chỉ khi ∃ k∈ℝ,k≠0 sao cho →AB = k→AC.
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
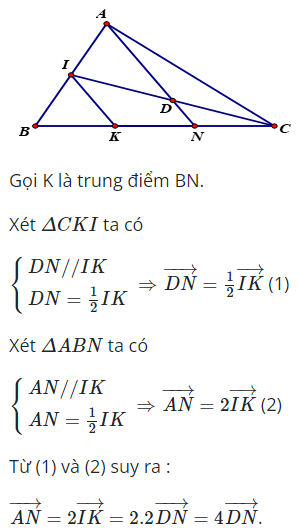
Lời giải
Ta có GA=23AM
Mặt khác →GA và →AM ngược hướng →GA=−23→AM.
Câu 3:
22/07/2024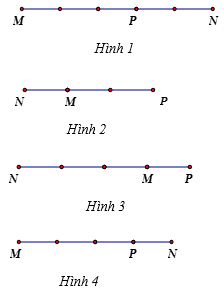
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có →MN=−3→MP nên MN=3MP và →MN và →MP ngược hướng.
Câu 4:
21/07/2024Cho ba điểm A,B,C phân biệt. Điều kiện cần và đủ để ba điểm đó thẳng hàng là
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có tính chất: Điều kiện cần và đủ để ba điểm A,B,C phân biệt thẳng hàng là ∃k∈R:→AB=k→AC.
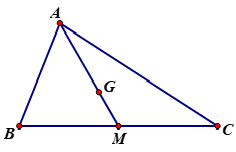
Câu 5:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
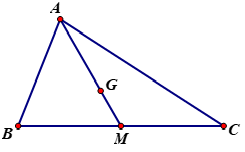
Do M là trung điểm của BC nên ta có →AM=12(→AB+→AC).
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
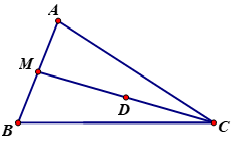
Ta có:
→DA+→DB+2→DC=2→DM+2→DC
=2(→DM+→DC)=2.→0=→0
Câu 7:
23/07/2024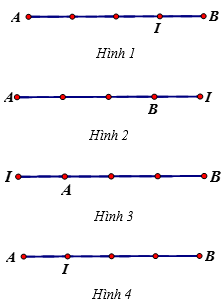
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có:
→IB+3→IA=→0⇔→IB=−3→IA
Do đó IB=3.IA; →IA và →IB ngược hướng. Chọn Hình 4.
Câu 8:
04/01/2025 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải
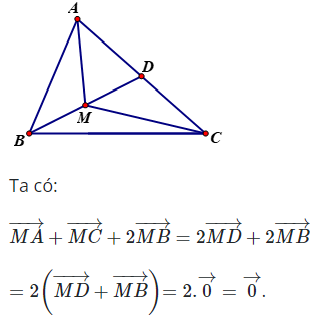
*Phương pháp giải:
Áp dụng quy tắc hình bình hành: Nếu ABCD là hình bình hành thì .
*Lý thuyết:
- Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:
→MA+→MB=2→MI ( M tùy ý )
→IA+→IB=→0
- Quy tắc trọng tâm: Với G là trọng tâm tam giác ABC thì ta có:
→MA+→MB+→MC=3→MG ( M tùy ý )
→GA+→GB+→GC=→0
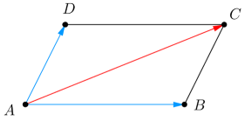
- Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì →AB+→AD=→AC.
- Quy tắc trung điểm: I là trung điểm của AB
→IA+→IB=→0
→MA+→MB=2→MI ( M tùy ý )
- Quy tắc trọng tâm: G là trọng tâm tam giác ABC
→MA+→MB+→MC=3→MG ( M tùy ý )
→GA+→GB+→GC=→0
- Quy tắc hình hình hành: →AB+→AD=→AC ( ABCD là hình bình hành )
Xem thêm
Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vecto chi tiết nhấtCâu 9:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có:
− → a +12→ b =12(−2 → a +→ b )=12→ x
Chọn B.
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
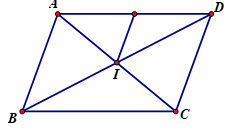
Ta có:
→MA+→MC=2→MI=→AB
Vậy M là trung điểm của AD .
Câu 11:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Gọi G là trọng tâm của tam giác ABC , ta có :
→MA+→MB+→MC=3→MG
Thay vào ta được :
|→MA+→MB+→MC|=6
⇔|3→MG|=6⇔MG=2
hay tập hợp các điểm M là đường tròn có tâm là trọng tâm của tam giác ABC và bán kính bằng 2 .
Câu 12:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có
5→MA=2→MB⇔5(→MI+→IA)
=2(→MI+→IB)⇔5→IA=3→IM+2→IB
⇔→IA=35→IM+25→IB
Câu 13:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
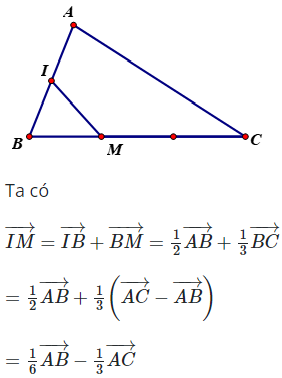
Câu 14:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có :
−12→a+→b=−12(→a−2→b)
nên chọn A
Câu 15:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
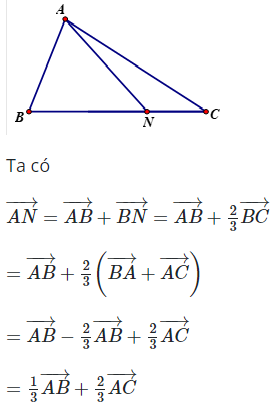
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có:
|→MA+→MB|=|→MA−→MB|
⇔|2→MI|=|→BA|
⇔2MI=BA⇔MI=BA2
Vậy tập hợp các điểm M là đường tròn đường kính AB.
Câu 17:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
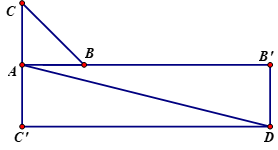
Vẽ AB'. Vẽ hình bình hành
Ta có:
Do đó
.
Câu 18:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
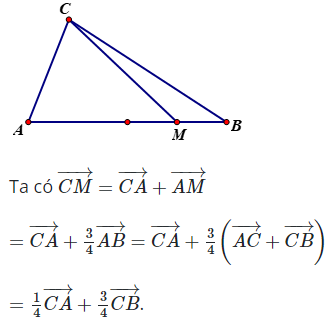
Câu 19:
13/07/2024Xét các phát biểu sau:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
(2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là
Trong các câu trên, thì:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là
Phát biểu sai: (2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
Do đó câu (1) và câu (3) là đúng.
Câu 20:
15/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
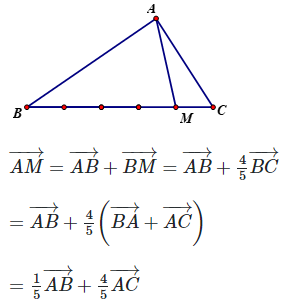
Câu 21:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
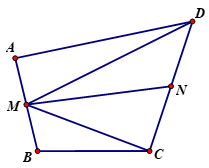
Do M là trung điểm các cạnh AB nên
Do N lần lượt là trung điểm các cạnh DC nên
Ta có
Mặt khác
Do đó:
Câu 22:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
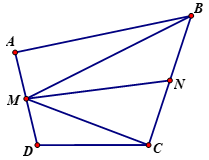
Do M là trung điểm các cạnh AD nên
Do N lần lượt là trung điểm các cạnh BC nên . Nên D đúng.
Ta có:
Vậy . Nên C đúng
Mà
Nên A đúng.
Vậy B sai.
Câu 23:
29/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải:
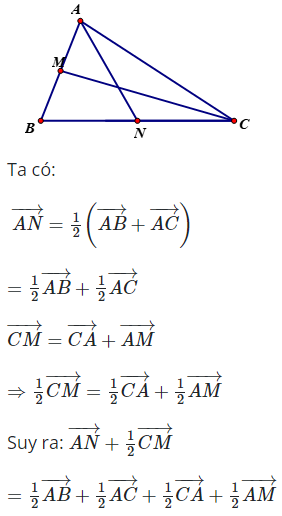
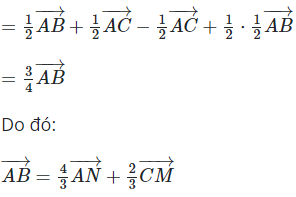
*Phương pháp giải:
- Nắm kỹ lý thuyết về vectơ và dạng bài tính tổng hiệu hai vecto. Tính chất trung điểm, đường trung bình, trung tuyến của tam giác để làm
*Một số dạng bài về tích của vectơ với một số
*Lý thuyết cần nắm:
- Tích của vectơ với một số: Cho số k0 và vectơ . Tích của vectơ với số k là một vectơ, kí hiệu là , cùng hướng với nếu k > 0, ngược lại, ngược hướng với nếu k < 0 và có độ dài bằng .
- Tính chất: Với hai vectơ và bất kì, với mọi số h và k, ta có:
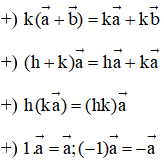
- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có:
- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có:
Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.
* Phương pháp giải: Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.
Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.
* Phương pháp giải: Biến đổi đẳng thức đã cho về dạng trong đó A là một điểm cố định, cố định và dựng điểm M là điểm thỏa mãn .
Xem thêm các bài viết liên quan hay, chi tiết
Câu 24:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
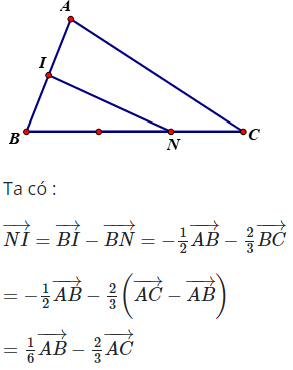
Có thể bạn quan tâm
- Trắc nghiệm Tích của vectơ với một số (có đáp án) (740 lượt thi)
- Trắc nghiệm Tích của vecto với một số có đáp án (562 lượt thi)
- Trắc nghiệm Tích của vectơ với một số có đáp án (Nhận biết) (817 lượt thi)
- Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu) (406 lượt thi)
- Trắc nghiệm Tích của vectơ với một số có đáp án (Vận dụng) (465 lượt thi)
Các bài thi hot trong chương
- 80 câu trắc nghiệm Vectơ cơ bản (2236 lượt thi)
- 75 câu trắc nghiệm Vectơ nâng cao (2005 lượt thi)
- Trắc nghiệm Các định nghĩa (có đáp án) (856 lượt thi)
- Trắc nghiệm Hệ trục tọa độ (có đáp án) (853 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ (có đáp án) (832 lượt thi)
- Trắc nghiệm Ôn tập chương 1 Hình học 10 (có đáp án) (803 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Thông hiểu) (565 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Vận dụng) (558 lượt thi)
- Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Tổng hợp) (457 lượt thi)
- Trắc nghiệm Các định nghĩa vecto có đáp án (440 lượt thi)