21 câu hỏi trắc nghiệm thuộc Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Tổng hợp)

Câu 1:

20/07/2024

Cho hình bình hành ABCD, với giao điểm hai đường chéo là I. Khi đó

A. $\vec{A B} + \vec{I A} = \vec{B I}$

B. $\vec{A B} + \vec{A D} = \vec{B D}$

C. $\vec{A B} + \vec{C D} = \vec{0}$

D. $\vec{A B} + \vec{B D} = \vec{0}$

Xem đáp án

Câu 2:

22/07/2024

Cho tam giác ABC và một điểm G thỏa mãn $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ . Chọn khẳng định đúng:

A. G là tâm đường tròn ngoại tiếp tam giác ABC

B. G là tâm đường tròn nội tiếp tam giác ABC

C. G là trực tâm tam giác ABC

D. G là trọng tâm tam giác ABC

Xem đáp án

Điểm G là trọng tâm tam giác ABC

Đáp án cần chọn là: D

Câu 3:

07/10/2024

Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?

A. $\vec{O A} - \vec{O B} = \vec{C D}$

B. $\vec{O B} - \vec{O C} = \vec{O D} - \vec{O A}$

C. $\vec{A B} - \vec{A D} = \vec{D B}$

D. $\vec{B C} - \vec{B A} = \vec{D C} - \vec{D A}$

Xem đáp án

Đáp án đúng: B

*Phương pháp giải:

- Nắm kỹ lý thuyết về vectơ và dạng bài tính tổng hiệu hai vecto và tính chất hình bình hành

*Lời giải:

Xét các đáp án:

Đáp án A. Ta có: . Vậy A đúng

Đáp án B. Ta có: Vậy B sai

Đáp án C. TA có: . Vậy C đúng

Đáp án D. Ta có: . Vậy D đúng

*Một số dạng bài về tích của vectơ với một số

*Lý thuyết cần nắm:

- Tích của vectơ với một số: Cho số k $\neq$ 0 và vectơ $\vec{a} \neq \vec{0}$ . Tích của vectơ $\vec{a}$ với số k là một vectơ, kí hiệu là $k \vec{a}$ , cùng hướng với $\vec{a}$ nếu k > 0, ngược lại, ngược hướng với $\vec{a}$ nếu k < 0 và có độ dài bằng $|k| |\vec{a}|$ .

- Tính chất: Với hai vectơ $\vec{a}$ và $\vec{b}$ bất kì, với mọi số h và k, ta có:

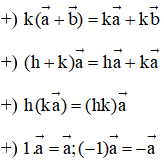
- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có: $\vec{M A} + \vec{M B} = 2 \vec{M I}$

- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có: $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.

* Phương pháp giải: Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.

Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.

* Phương pháp giải: Biến đổi đẳng thức đã cho về dạng $\vec{A M} = \vec{u}$ trong đó A là một điểm cố định, $\vec{u}$ cố định và dựng điểm M là điểm thỏa mãn $\vec{A M} = \vec{u}$ .

Xem thêm các bài viết liên quan hay, chi tiết

Chuyên đề Vectơ lớp 10 (có đáp án)

Trắc nghiệm Tổng hiệu của hai vecto có đáp án – Toán lớp 10

Trắc nghiệm Tích của vecto với một số có đáp án – Toán lớp 10

Câu 4:

22/11/2024

Cho I là trung điểm AB. Với mỗi điểm M bất kì ta luôn có

A. $\vec{M I} = \vec{M A} + \vec{M B}$

B. $\vec{M I} = 2 (\vec{M A} + \vec{M B)}$

C. $\vec{M I} = \frac{1}{2} (\vec{M A} + \vec{M B)}$

D. $\vec{M I} = 2 \vec{M A} + \vec{M B}$

Xem đáp án

Đáp án đúng: C

* Lời giải:

Với mỗi điểm M bất kì và I là trung điểm của đoạn thẳng AB thì hay

* Phương pháp giải:

Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi $\vec{M A} + \vec{M B} = \vec{0}$ .

Và do I là trung điểm trên đoạn AB nên với mỗi M bất kì ta sẽ suy ra được:

*Một số lý thuyết và dạng bài tập về tổng và hiệu của hai vectơ

1. Tổng của hai vectơ

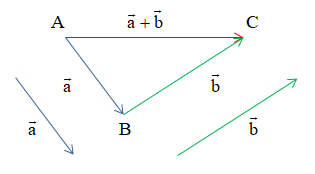
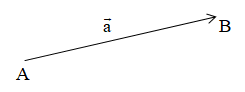
Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ . Khi đó $\vec{A C}$ được gọi là tổng của hai vectơ $\vec{a}$ và $\vec{b}$ và được kí hiệu là $\vec{a} + \vec{b}$ .

Vậy $\vec{a} + \vec{b} = \vec{A B} + \vec{B C} = \vec{A C}$ .

Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.

Quy tắc ba điểm

Với ba điểm M, N, P, ta có $\vec{M N} + \vec{N P} = \vec{M P}$ .

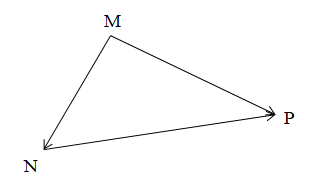Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.

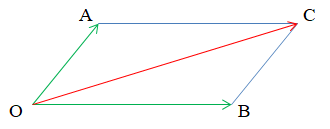
Quy tắc hình bình hành

Nếu OACB là hình bình hành thì ta có $\vec{O A} + \vec{O B} = \vec{O C}$ .

2. Tính chất của phép cộng các vectơ

Phép cộng vectơ có các tính chất sau:

+ Tính chất giao hoán: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$ .

+ Tính chất kết hợp: $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$ .

+ Với mọi $\vec{a}$ , ta luôn có: $\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$ .

Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ $\vec{a}, \vec{b}, \vec{c}$ ,kí hiệu là $\vec{a} + \vec{b} + \vec{c}$ với $\vec{a} + \vec{b} + \vec{c} = (\vec{a} + \vec{b}) + \vec{c}$ .

Chú ý: Cho vectơ tùy ý $\vec{a} = \vec{A B}$ .

Ta có $\vec{a} + (- \vec{a}) = \vec{A B} + (- \vec{A B}) = \vec{A B} + \vec{B A} = \vec{A A} = \vec{0}$ .

Tổng hai vectơ đối nhau luôn bằng vectơ-không: $\vec{a} + (- \vec{a}) = \vec{0}$ .

3. Hiệu của hai vectơ

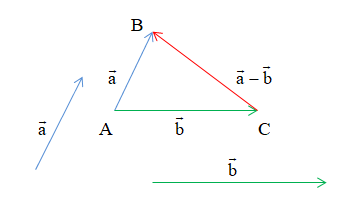
Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Hiệu của hai vectơ $\vec{a}$ và $\vec{b}$ là vectơ \ $\vec{a} + (- \vec{b})$ và kí hiệu là $\vec{a} - \vec{b}$ .

Phép toán tìm hiệu của hai vectơ được gọi là phép trừ vectơ.

4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi $\vec{M A} + \vec{M B} = \vec{0}$ .

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

Xem thêm các bài viết liên quan hay, chi tiết

Lý thuyết Tổng và hiệu của hai vectơ – Toán 10 Chân trời sáng tạo

Giải Toán 10 Bài 8 (Kết nối tri thức): Tổng và hiệu của hai vectơ

Câu 5:

10/07/2024

Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là

A. IA=IB

B. $\vec{I A} = \vec{I B}$

C. $\vec{I A} + \vec{I B} = \vec{0}$

D. $\vec{A I} = \vec{B I}$

Xem đáp án

I là trung điểm của AB nếu $\vec{I A} + \vec{I B} = \vec{0}$

Đáp án cần chọn là: C

Câu 6:

23/07/2024

Cho 6 điểm A, B, C, D, E, F. Đẳng thức nào sau đây đúng?

A. $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C}$ $+ \vec{E F} + \vec{D E} = \vec{0}$

B. $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C}$ $+ \vec{E F} + \vec{D E} = \vec{A F}$

C. $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C}$ $+ \vec{E F} + \vec{D E} = \vec{A E}$

D. $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C}$ $+ \vec{E F} + \vec{D E} = \vec{A D}$

Xem đáp án

Ta có:

Đáp án cần chọn là: A

Câu 7:

17/07/2024

Tính tổng: $\vec{M N} + \vec{P Q} + \vec{R N} + \vec{N P} + \vec{Q R}$

A. $\vec{M R}$

B. $\vec{M N}$

C. $\vec{P R}$

D. $\vec{M P}$

Xem đáp án

Câu 8:

14/07/2024

Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC = 24. Tính độ dài của vec tơ $|\vec{v}| = \vec{G B} + \vec{G C}$

A. $|\vec{v}| = 2$

B. $|\vec{v}| = 2 \sqrt{3}$

C. $|\vec{v}| = 8$

D. $|\vec{v}| = 4$

Xem đáp án

Dựng hình bình hành GBDC. Gọi M là trung điểm BC.

Khi đó ta có

Đáp án cần chọn là: C

Câu 9:

22/07/2024

Cho hình thoi ABCD tâm O, cạnh bằng a và góc A bằng $60 °$ . Kết luận nào sau đây đúng

A. $|\overset{⇀}{O A}| = \frac{a \sqrt{3}}{2}$

B. $|\overset{⇀}{O A}| = a$

C. $|\overset{⇀}{O A}| = |\overset{⇀}{O B}|$

D. $|\overset{⇀}{O A}| = \frac{a \sqrt{2}}{2}$

Xem đáp án

Do nên tam giác ABD đều

Do đó

Đáp án cần chọn là: A

Câu 10:

11/10/2024

Cho hình vuông ABCD cạnh a, tâm O. Khi đó $|\vec{O A} + \vec{O B}|$

A. a

B. $\sqrt{2} a$

C. $\frac{a}{2}$

D. 2a

Xem đáp án

Đáp án đúng: A

*Phương pháp giải:

- Nắm kỹ lý thuyết về tính chất gioa điểm 2 đường chéo hình bình hành và vận dụng vào vecto

*Lời giải:

Dựng hình bình hành OAEB và gọi M là giao điểm của AB và OE.

Ta có:

*Một số lý thuyết nắm thêm về tổng/hiệu vecto và độ dài vecto

Độ dài của vectơ là độ dài đoạn thẳng tạo bởi điểm đầu và điểm cuối của vectơ đó.

$|\vec{A B}| = |\vec{B A}| = A B = B A$ .

- Quy tắc ba điểm: Với 3 điểm A, B, C ta luôn $\vec{A B} + \vec{B C} = \vec{A C}$ , $\vec{A C} - \vec{A B} = \vec{B C}$ .

- Quy tắc hình bình hành: Cho hình bình hành ABCD, ta có $\vec{A C} = \vec{A B} + \vec{A D}$ .

- Quy tắc trung điểm: $\vec{I A} + \vec{I B} = \vec{0}$ với I là trung điểm của AB.

- Quy tắc trọng tâm: $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ với G là trọng tâm của tam giác ABC.

Xem thêm các bài viết liên quan hay, chi tiết

Chuyên đề Vectơ lớp 10 (có đáp án)

Trắc nghiệm Tổng hiệu của hai vecto có đáp án – Toán lớp 10

Trắc nghiệm Tích của vecto với một số có đáp án – Toán lớp 10

Câu 11:

22/07/2024

Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?

A. $\vec{O A} + \vec{O C} + \vec{O E} = \vec{0}$

B. $\vec{O B} + \vec{O D} + \vec{O F} = \vec{0}$

C. $\vec{O A} + \overset{⇀}{O B} + \vec{O C} = \vec{E B}$

D. $\vec{A B} + \vec{C D} + \vec{F E} = \vec{A D}$

Xem đáp án

Câu 12:

17/07/2024

Cho $∆ A B C$ vuông tại A và AB = 3, AC = 4. Vec tơ $\vec{C B} + \vec{A B}$ có độ dài bằng

A. $\sqrt{13}$

B. $2 \sqrt{13}$

C. $2 \sqrt{3}$

D. $\sqrt{3}$

Xem đáp án

Dựng hình bình hành ABCD tâm E

Ta có:

Đáp án cần chọn là: B

Câu 13:

15/07/2024

Cho tam giác ABC. Để điểm M thoả mãn điều kiện $\vec{M A} + \vec{B M} + \vec{M C} = \vec{0}$ thì M phải thỏa mãn mệnh đề nào?

A. M là điểm sao cho tứ giác ABMC là hình bình hành

B. M là trọng tâm tam giác ABC

C. M là điểm sao cho tứ giác BAMClà hình bình hành

D. M thuộc trung trực của AB

Xem đáp án

Vậy M là điểm sao cho tứ giác BAMClà hình bình hành.

Đáp án cần chọn là: C

Câu 14:

11/07/2024

Cho tam giác ABC và điểm M thỏa mãn $\vec{M B} + \vec{M C} = \vec{A B}$ . Tìm vị trí điểm M

A. M là trung điểm của AC

B. M là trung điểm của AB

C. M là trung điểm của BC

D. M là điểm thứ tư của hình bình hành ABCM

Xem đáp án

Câu 15:

21/07/2024

Cho hình thang ABCD có AB song song với CD. Cho AB = 2a; CD = a. Gọi O là trung điểm của AD. Khi đó

A. $|\vec{O B} + \vec{O C}| = a$

B. $|\vec{O B} + \vec{O C}| = \frac{3 a}{2}$

C. $|\vec{O B} + \vec{O C}| = 2 a$

D. $|\vec{O B} + \vec{O C}| = 3 a$

Xem đáp án

Dựng hình bình hành OBFC tâm E. Khi đó

Đáp án cần chọn là: D

Câu 16:

17/07/2024

Cho hình vuông ABCD có cạnh bằng a. Khi đó $|\vec{A B} + \vec{A C}|$ bằng

A. $\frac{a \sqrt{5}}{2}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{a \sqrt{3}}{3}$

D. $a \sqrt{5}$

Xem đáp án

Câu 17:

22/07/2024

Cho tam giác ABC và điểm M thỏa mãn điều kiện $\vec{M A} + \vec{M C} = \vec{M B}$ . Mệnh đề nào sau đây sai?

A. MABC là hình bình hành

B. $\vec{A M} + \vec{A B} = \vec{A C}$

C. $\vec{B A} + \vec{B C} = \vec{B M}$

D. $\vec{M A} = \vec{B C}$

Xem đáp án

Ta có nên MABC là hình bình hành

Do đó D sai

Đáp án cần chọn là: D

Câu 18:

19/07/2024

Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng

A. $\vec{C A} - \vec{B A} = \vec{B C}$

B. $\vec{A B} + \vec{A C} = \vec{B C}$

C. $\vec{A B} + \vec{C A} = \vec{C B}$

D. $\vec{A B} - \vec{B C} = \vec{C A}$

Xem đáp án

Xét các đáp án:

Đáp án A: Ta có Vậy A sai

Đáp án B. Ta có (với D là điểm thỏa mãn ABDC là hình bình hành). Vậy B sai.

Đáp án C. Ta có . Vậy C đúng

Đáp án cần chọn là: C

Câu 19:

12/10/2024

Cho tam giác ABC vuông cân đỉnh A, đường cao AH. Khẳng định nào sau đây sai

A. $|\vec{A H} + \vec{H B}| = |\vec{A H} + \vec{H C}|$

B. $\vec{A H} - \vec{A B} = \vec{A H} - \vec{A C}$

C. $\vec{B C} - \vec{B A} = \vec{H C} - \vec{H A}$

D. $|\vec{A H}| = |\vec{A B} - \vec{A H}|$

Xem đáp án

Đáp án đúng: B

*Phương pháp giải:

- Nắm kỹ lý thuyết về vectơ và dạng bài tính tổng hiệu hai vecto

*Lời giải:

Do $∆ A B C$ cân tại A, AH là đường cao nên H là trung điểm BC

Xét các đáp án:

Đáp án A. Ta có:

Đáp án B. Ta có:

Do đó B sai

Đáp án C. Ta có:

Đáp án D. Ta có:

(do $∆ A B C$ vuông cân tại A)

*Một số dạng bài về tích của vectơ với một số

*Lý thuyết cần nắm:

- Định nghĩa hiệu của hai vectơ: Cho hai vectơ $\vec{a}$ , $\vec{b}$ tùy ý. Ta có: $\vec{a} - \vec{b} = \vec{a} + (- \vec{b})$ .

- Tính chất của phép cộng :

+) $\vec{a} + \vec{b} = \vec{b} + \vec{a}$ ( giao hoán )

+) $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$ ( kết hợp )

+) $\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$

- Vectơ đối: $\vec{a} = - \vec{b} \Leftrightarrow |\vec{a}| = |\vec{b}|$ và $\vec{a}$ ngược hướng với $\vec{b}$

- Hiệu hai vectơ: $\vec{a} - \vec{b} = \vec{a} + (- \vec{b})$ .

- Độ dài vectơ tổng, hiệu:

$\vec{u} = \vec{a} + \vec{b} \Rightarrow |\vec{u}| = |\vec{a} + \vec{b}| \vec{v} = \vec{a} - \vec{b} \Rightarrow |\vec{v}| = |\vec{a} - \vec{b}|$ $\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$

- Quy tắc ba điểm: Với A, B, C tùy ý

$\vec{A B} + \vec{B C} = \vec{A C}$ (đối với tổng)

$\vec{A B} - \vec{A C} = \vec{C B}$ (đối với hiệu)

- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có: $\vec{M A} + \vec{M B} = 2 \vec{M I}$

- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có: $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.

* Phương pháp giải: Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.

Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.

* Phương pháp giải: Biến đổi đẳng thức đã cho về dạng $\vec{A M} = \vec{u}$ trong đó A là một điểm cố định, $\vec{u}$ cố định và dựng điểm M là điểm thỏa mãn $\vec{A M} = \vec{u}$

$\vec{A M} = \vec{u}$

Công thức về tổng và hiệu hai vectơ (2024) và cách giải các dạng bài tập $\vec{A M} = \vec{u}$ $\vec{A M} = \vec{u}$ $\vec{A M} = \vec{u}$ $\vec{A M} = \vec{u}$

$\vec{A M} = \vec{u}$

Câu 20:

23/07/2024

Chỉ ra vec tơ tổng $\vec{M N} - \vec{Q P} + \vec{R N} - \vec{P N} + \vec{Q R}$ trong các vec tơ sau

A. $\vec{M R}$

B. $\vec{M Q}$

C. $\vec{M P}$

D. $\vec{M N}$

Xem đáp án

Câu 21:

21/07/2024

Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Hỏi vec tơ $\vec{A O} - \vec{D O}$ bằng vec tơ nào trong các vec tơ sau?

A. $\vec{B A}$

B. $\vec{B C}$

C. $\vec{D C}$

D. $\vec{A C}$

Xem đáp án

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3