Trắc nghiệm Tích của vectơ với một số có đáp án (Nhận biết)
-
752 lượt thi
-
11 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Chọn phát biểu sai?
Xem đáp án
Ta có ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi các vec tơ cùng phương, hay sao cho hoặc
Chú ý rằng hệ số k phải khác 0 nên chỉ có đáp án D sai
Đáp án cần chọn là: D
Câu 2:
23/07/2024Cho vectơ . Khẳng định nào sau đây sai
Xem đáp án
Ta có:
Vậy hai vectơ đối nhau.
Do đó chúng cùng phương, ngược hướng nên các đáp án B, C, D đúng.
Đáp án A sai vì hai véc tơ đó không bằng nhau.
Đáp án cần chọn là: A
Câu 3:
23/07/2024Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó
Xem đáp án
Ta có: 
Mặt khác 
ngược hướng 
Đáp án cần chọn là: C
Câu 4:
12/10/2024Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án đúng: D
*Phương pháp giải:
- Áp dụng tính chất trọng tâm trong tam giác suy ra tỷ số AG=2/3 AM
- Xét hướng của 2 vectơ GA và GM
*Lời giải:
*Một số lý thuyết nắm thêm về tổng/hiệu vecto và độ dài vecto
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.
- Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ và cùng phương.
* Các quy tắc về vectơ:
Độ dài của vectơ là độ dài đoạn thẳng tạo bởi điểm đầu và điểm cuối của vectơ đó.
.
- Quy tắc ba điểm: Với 3 điểm A, B, C ta luôn , .
- Quy tắc hình bình hành: Cho hình bình hành ABCD, ta có .
- Quy tắc trung điểm: với I là trung điểm của AB.
- Quy tắc trọng tâm: với G là trọng tâm của tam giác ABC.
Tính chất phép cộng vecto:
+ Tính chất giao hoán: .
+ Tính chất kết hợp: .
+ Với mọi , ta luôn có: .
Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ ,kí hiệu là với .
Xem thêm các bài viết liên quan hay, chi tiết
80 câu trắc nghiệm Vectơ cơ bản
Trắc nghiệm Tích của vecto với một số có đáp án – Toán lớp 10
Câu 5:
20/07/2024Trên đường thẳng MN lấy điểm P sao cho . Điểm P được xác định đúng trong hình vẽ nào sau đây:
Xem đáp án
Ta có 
nên MN+3MP và 
ngược hướng
Đáp án cần chọn là: C
Câu 6:
21/07/2024Hãy chọn kết quả đúng khi phân tích vec tơ theo hai vec tơ của tam giác ABC với trung tuyến AM
Xem đáp án
Do M là trung điểm của BC nên ta có
Đáp án cần chọn là: C
Câu 7:
23/07/2024Đẳng thức nào sau đây mô tả đúng hình vẽ bên:
Xem đáp án
Ta có:
ngược hướng nên
Vậy 
Đáp án cần chọn là: A
Câu 9:
22/07/2024Cho hai tam giác ABC và A’B’C’ lần lượt có trọng tâm G và G’. Đẳng thức nào sau đây là sai?
Xem đáp án
Do G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’ nên
và 
Đáp án A:
Đáp án B:
Đáp án C:
Đáp án D:
Đáp án cần chọn là: D
Câu 10:
23/11/2024Cho tam giác ABC và một điểm M tùy ý. Mệnh đề nào sau đây đúng?
Xem đáp án
Đáp án đúng: C
* Lời giải:
* Phương pháp giải:
- Áp dụng tính chất về tích, tổng và hiệu hai vectơ để biến đổi và thực hiện phép tính
*Một số lý thuyết và dạng bài tập về tích của vectơ:
- Tích của vectơ với một số: Cho số k0 và vectơ . Tích của vectơ với số k là một vectơ, kí hiệu là , cùng hướng với nếu k > 0, ngược lại, ngược hướng với nếu k < 0 và có độ dài bằng .
- Tính chất: Với hai vectơ và bất kì, với mọi số h và k, ta có:
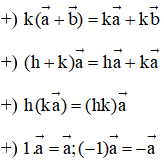
- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có:
- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có:
- Điều kiện để hai vectơ cùng phương: Cho hai vectơ và () , và cùng phương khi và chỉ khi tồn tại số k để .
- Điều kiện ba điểm thẳng hàng: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có tồn tại một số k khác 0 để .
- Chú ý: Đối với vectơ – không : ;
Các dạng bài.
Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.
Phương pháp giải:
Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.
Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.
Phương pháp giải:
Biến đổi đẳng thức đã cho về dạng trong đó A là một điểm cố định, cố định và dựng điểm M là điểm thỏa mãn .
Xem thêm các bài viết liên quan hay, chi tiết
Tích của vectơ với một số và cách giải bài tập (2024) chi tiết nhất
Giải Toán 10 Bài 5 (Cánh diều): Tích của một số với một vectơ
Câu 11:
18/07/2024Cho hai vec tơ không cùng phương. Hai vec tơ nào sau đây cùng phương
Xem đáp án
Ta có 
nên chọn đáp án C
Đáp án cần chọn là: C