Cho tam giác ABC và một điểm M tùy ý. Mệnh đề nào sau đây đúng?

Đáp án đúng: C

* Lời giải:

* Phương pháp giải:

- Áp dụng tính chất về tích, tổng và hiệu hai vectơ để biến đổi và thực hiện phép tính

*Một số lý thuyết và dạng bài tập về tích của vectơ: 

- Tích của vectơ với một số: Cho số k$\ne$0 và vectơ $\overrightarrow{a}\ne \overrightarrow{0}$. Tích của vectơ $\overrightarrow{a}$ với số k là một vectơ, kí hiệu là $k\overrightarrow{a}$, cùng hướng với $\overrightarrow{a}$ nếu k > 0, ngược lại, ngược hướng với $\overrightarrow{a}$ nếu k < 0 và có độ dài bằng $\left|k\right|\left|\overrightarrow{a}\right|$.

- Tính chất: Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bất kì, với mọi số h và k, ta có:

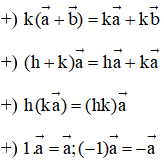
- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có: $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$

- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có:

$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$

- Điều kiện để hai vectơ cùng phương: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ ($\overrightarrow{b}\ne \overrightarrow{0}$) ,$\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương khi và chỉ khi tồn tại số k để $\overrightarrow{a}=k\overrightarrow{b}$.

- Điều kiện ba điểm thẳng hàng: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có tồn tại một số k khác 0 để $\overrightarrow{AB}=k\overrightarrow{AC}$.

- Chú ý: Đối với vectơ – không : $0.\overrightarrow{a}=\overrightarrow{0}$; $k.\overrightarrow{0}=\overrightarrow{0}$

Các dạng bài.

Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.

Phương pháp giải:

Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.

Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.

Phương pháp giải:

 

Biến đổi đẳng thức đã cho về dạng $\overrightarrow{AM}=\overrightarrow{u}$ trong đó A là một điểm cố định, $\overrightarrow{u}$ cố định và dựng điểm M là điểm thỏa mãn $\overrightarrow{AM}=\overrightarrow{u}$.

Xem thêm các bài viết liên quan hay, chi tiết

Tích của vectơ với một số và cách giải bài tập (2024) chi tiết nhất

Giải Toán 10 Bài 5 (Cánh diều): Tích của một số với một vectơ 

Trắc nghiệm Tích của vecto với một số có đáp án – Toán lớp 10